|
Helmholtz Centre In Geesthacht
Hermann Ludwig Ferdinand von Helmholtz (31 August 1821 – 8 September 1894) was a German physicist and physician who made significant contributions in several scientific fields, particularly hydrodynamic stability. The Helmholtz Association, the largest German association of research institutions, is named in his honor. In the fields of physiology and psychology, Helmholtz is known for his mathematics concerning the eye, theories of vision, ideas on the visual perception of space, color vision research, the sensation of tone, perceptions of sound, and empiricism in the physiology of perception. In physics, he is known for his theories on the conservation of energy, work in electrodynamics, chemical thermodynamics, and on a mechanical foundation of thermodynamics. As a philosopher, he is known for his philosophy of science, ideas on the relation between the laws of perception and the laws of nature, the science of aesthetics, and ideas on the civilizing power of science ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potsdam
Potsdam () is the capital and, with around 183,000 inhabitants, largest city of the German state of Brandenburg. It is part of the Berlin/Brandenburg Metropolitan Region. Potsdam sits on the River Havel, a tributary of the Elbe, downstream of Berlin, and lies embedded in a hilly morainic landscape dotted with many lakes, around 20 of which are located within Potsdam's city limits. It lies some southwest of Berlin's city centre. The name of the city and of many of its boroughs are of Slavic origin. Potsdam was a residence of the Prussian kings and the German Kaiser until 1918. Its planning embodied ideas of the Age of Enlightenment: through a careful balance of architecture and landscape, Potsdam was intended as "a picturesque, pastoral dream" which would remind its residents of their relationship with nature and reason. The city, which is over 1000 years old, is widely known for its palaces, its lakes, and its overall historical and cultural significance. Landmarks include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johannes Von Kries
Johannes Adolf von Kries (6 October 1853 – 30 December 1928) was a German physiological psychologist who formulated the modern “duplicity” or “duplexity” theory of vision mediated by rod cells at low light levels and three types of cone cells at higher light levels. He made important contributions in the field of haemodynamics. In addition, von Kries was a significant theorist of the foundations of probability. Biography When von Kries was at Freiburg (1880–1924), he was called to succeed Professor Emil Du Bois-Reymond as chair of physiology at the University of Berlin, but he declined. Von Kries has been called Helmholtz's "greatest German disciple". Works “Über den Druck in den Blutcapillaren der menschlichen Haut” ''Arbeiten aus der Physiologischen Anstalt zu Leipzig'' p 69-80 (1875). “Die Zeitdauer einfachster psychischer Vorgänge”with Felix Auerbach. ''Archiv für Physiologie'' p 297-378 (1877). * “Über die Bestimmung des Mitteldruckes durch d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Reciprocity
The Helmholtz reciprocity principle describes how a ray of light and its reverse ray encounter matched optical adventures, such as reflections, refractions, and absorptions in a passive medium, or at an interface. It does not apply to moving, non-linear, or magnetic media. For example, incoming and outgoing light can be considered as reversals of each other,Hapke, B. (1993). ''Theory of Reflectance and Emittance Spectroscopy'', Cambridge University Press, Cambridge UK, , Section 10C, pages 263-264. without affecting the bidirectional reflectance distribution function (BRDF) outcome. If light was measured with a sensor and that light reflected on a material with a BRDF that obeys the Helmholtz reciprocity principle one would be able to swap the sensor and light source and the measurement of flux would remain equal. In the computer graphics scheme of global illumination, the Helmholtz reciprocity principle is important if the global illumination algorithm reverses light paths ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Pitch Notation
Helmholtz pitch notation is a system for naming musical notes of the Western chromatic scale. Fully described and normalized by the German scientist Hermann von Helmholtz, it uses a combination of upper and lower case letters (A to G), and the sub- and super-prime symbols ( ͵ ′ or ) to denote each individual note of the scale. It is one of two formal systems for naming notes in a particular octave, the other being scientific pitch notation. History Helmholtz proposed this system in order to accurately define pitches in his classical work on acoustics ''Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik'' (1863) translated into English by A.J. Ellis as ''On the Sensations of Tone'' (1875). Helmholtz based his notation on the practice of German organ builders for labelling their pipes, itself derived from the old German organ tablature in use from late medieval times until the early 18th century. His system is widely use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
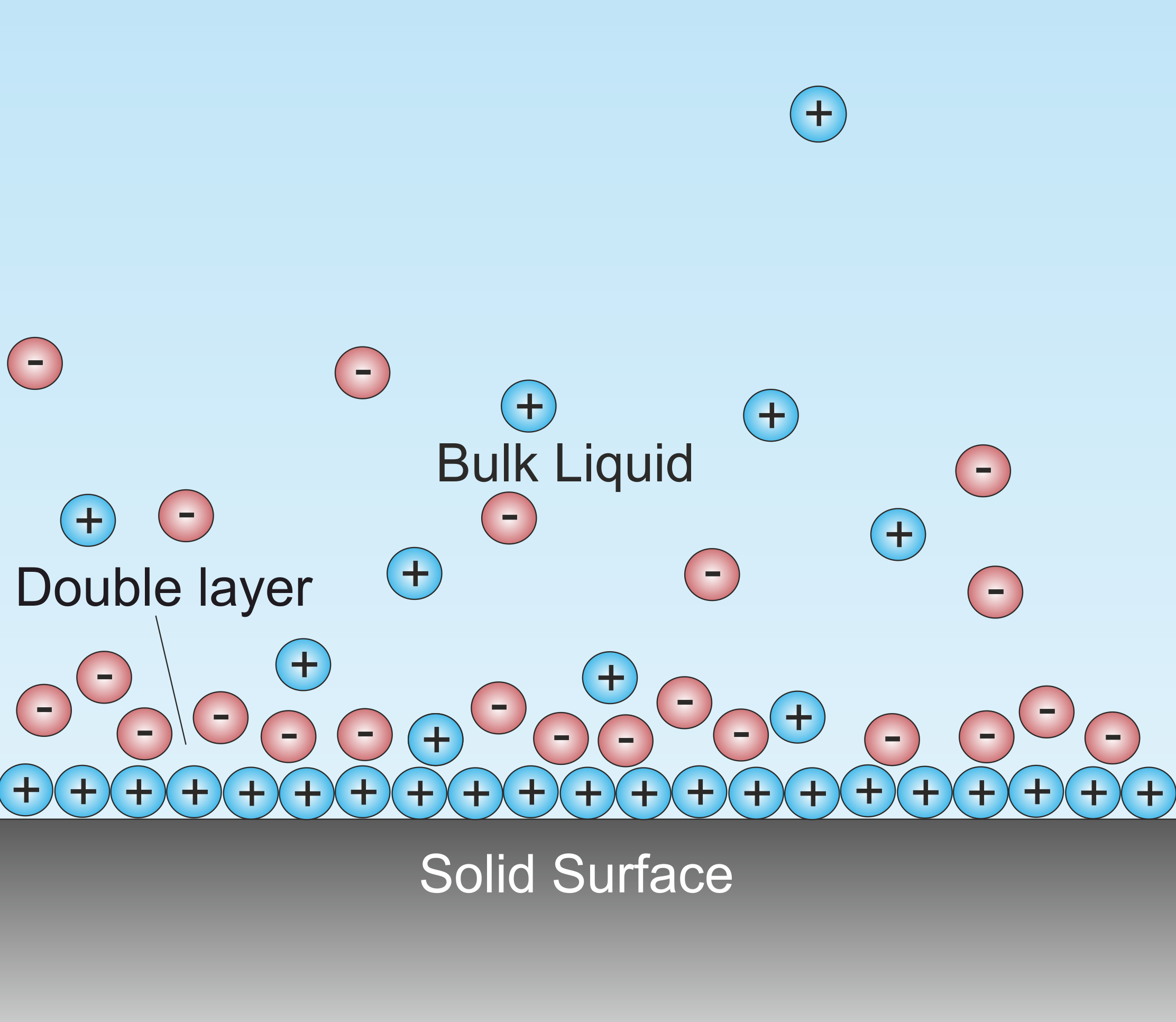
Helmholtz Layer
A double layer (DL, also called an electrical double layer, EDL) is a structure that appears on the surface of an object when it is exposed to a fluid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge (either positive or negative), consists of ions adsorbed onto the object due to chemical interactions. The second layer is composed of ions attracted to the surface charge via the Coulomb force, electrically screening the first layer. This second layer is loosely associated with the object. It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the "diffuse layer". Interfacial DLs are most apparent in systems with a large surface area to volume ratio, such as a colloid or porous bodies with particles or pores (respectively) on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Entropy
A thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy. Also known as a Massieu, Planck, or Massieu–Planck potentials (or functions), or (rarely) free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function. The Onsager reciprocal relations in particular, are developed in terms of entropic potentials. In mathematics, free entropy means something quite different: it is a generalization of entropy defined in the subject of free probability. A free entropy is generated by a Legendre transformation of the entropy. The different potentials correspond to different constraints to which the system may be subjected. Examples The most common examples are: where ::S is entropy ::\Phi is the Massieu potential ::\Xi is the Planck potential ::U is internal energy ::T is temperature ::P is pressure ::V is volume ::A is Helmholtz free energy ::G is Gibbs free energy ::N_i is number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Free Energy
In thermodynamics, the Helmholtz free energy (or Helmholtz energy) is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and ...). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium. In contrast, the Gibbs free energy or free enthalpy is most commonly used as a measure of thermodynamic potential (especially in chemistry) when it is convenient for applications that occur at constant ''pressure''. For example, in explosives research Helmholtz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Equation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation \nabla^2 f = -k^2 f, where is the Laplace operator (or "Laplacian"), is the eigenvalue, and is the (eigen)function. When the equation is applied to waves, is known as the wave number. The Helmholtz equation has a variety of applications in physics, including the wave equation and the diffusion equation, and it has uses in other sciences. Motivation and uses The Helmholtz equation often arises in the study of physical problems involving partial differential equations (PDEs) in both space and time. The Helmholtz equation, which represents a time-independent form of the wave equation, results from applying the technique of separation of variables to reduce the complexity of the analysis. For example, consider the wave equation \left(\nabla^2-\frac\frac\right) u(\mathbf,t)=0. Separation of variables begins by assumi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational ( curl-free) vector field and a solenoidal (divergence-free) vector field; this is known as the Helmholtz decomposition or Helmholtz representation. It is named after Hermann von Helmholtz. As an irrotational vector field has a scalar potential and a solenoidal vector field has a vector potential, the Helmholtz decomposition states that a vector field (satisfying appropriate smoothness and decay conditions) can be decomposed as the sum of the form -\nabla \phi + \nabla \times \mathbf, where \phi is a scalar field called "scalar potential", and is a vector field, called a vector potential. Statement of the theorem Let \mathbf be a vector field on a bounded domain V\subseteq\mathbb^3, which is twice continuousl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Condition
In mathematics, the inverse problem for Lagrangian mechanics is the problem of determining whether a given system of ordinary differential equations can arise as the Euler–Lagrange equations for some Lagrangian function. There has been a great deal of activity in the study of this problem since the early 20th century. A notable advance in this field was a 1941 paper by the American mathematician Jesse Douglas, in which he provided necessary and sufficient conditions for the problem to have a solution; these conditions are now known as the Helmholtz conditions, after the German physicist Hermann von Helmholtz. Background and statement of the problem The usual set-up of Lagrangian mechanics on ''n''-dimensional Euclidean space R''n'' is as follows. Consider a differentiable path ''u'' : , ''T''nbsp;→ R''n''. The action of the path ''u'', denoted ''S''(''u''), is given by :S(u) = \int_^ L(t, u(t), \dot(t)) \, \mathrm t, where ''L'' is a function of time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Coil
A Helmholtz coil is a device for producing a region of nearly uniform magnetic field, named after the German physicist Hermann von Helmholtz. It consists of two electromagnets on the same axis, carrying an equal electric current in the same direction. Besides creating magnetic fields, Helmholtz coils are also used in scientific apparatus to cancel external magnetic fields, such as the Earth's magnetic field. When the pair of two electromagnetics of a Helmholtz coil carry an equal electric current in the opposite direction, it is known as anti-Helmholtz coil, which creates a region of nearly uniform magnetic field gradient, and is used for creating magnetic traps for atomic physics experiments. Description A Helmholtz pair consists of two identical circular magnetic coils that are placed symmetrically along a common axis, one on each side of the experimental area, and separated by a distance h equal to the radius R of the coil. Each coil carries an equal electric current in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Energy
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be ''conserved'' over time. This law, first proposed and tested by Émilie du Châtelet, means that energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another. For instance, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If one adds up all forms of energy that were released in the explosion, such as the kinetic energy and potential energy of the pieces, as well as heat and sound, one will get the exact decrease of chemical energy in the combustion of the dynamite. Classically, conservation of energy was distinct from conservation of mass. However, special relativity shows that mass is related to energy and vice versa by ''E = mc2'', and science now takes the view that mass-energy as a whole is conserved. Theoretically, this implies that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |