|
Good Cover (algebraic Topology)
In mathematics, an open cover of a topological space X is a family of open subsets such that X is the union of all of the open sets. A good cover is an open cover in which all sets and all non-empty intersections of finitely-many sets are contractible . The concept was introduced by André Weil in 1952 for differentiable manifolds, demanding the U_ to be differentiably contractible. A modern version of this definition appears in . Application A major reason for the notion of a good cover is that the Leray spectral sequence of a fiber bundle degenerates for a good cover, and so the Čech cohomology associated with a good cover is the same as the Čech cohomology of the space. (Such a cover is known as a Leray cover.) However, for the purposes of computing the Čech cohomology it suffices to have a more relaxed definition of a good cover in which all intersections of finitely many open sets have contractible connected components. This follows from the fact that higher derived funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
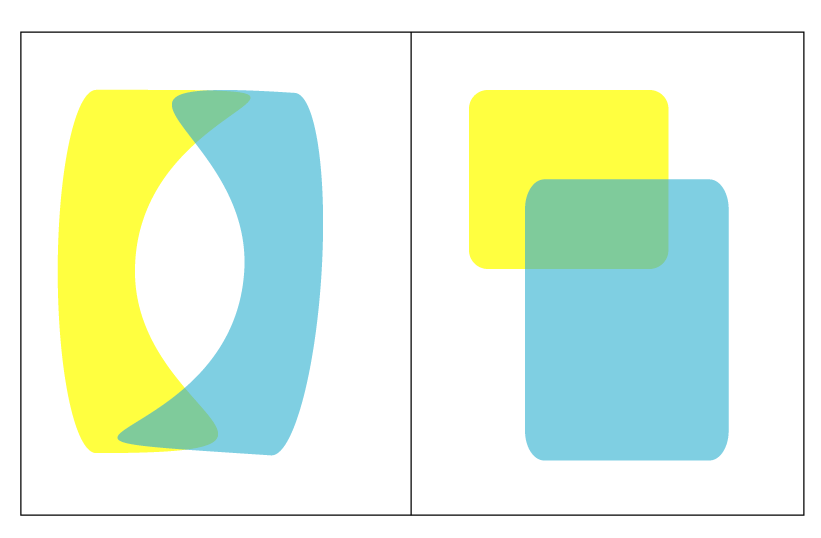
Good And "bad" Covers
In most contexts, the concept of good denotes the conduct that should be preferred when posed with a choice between possible actions. Good is generally considered to be the opposite of evil and is of interest in the study of ethics, morality, philosophy, and religion. The specific meaning and etymology of the term and its associated translations among ancient and contemporary languages show substantial variation in its inflection and meaning, depending on circumstances of place and history, or of philosophical or religious context. History of Western ideas Every language has a word expressing ''good'' in the sense of "having the right or desirable quality" ( ἀρετή) and ''bad'' in the sense "undesirable". A sense of moral judgment and a distinction "right and wrong, good and bad" are cultural universals. Plato and Aristotle Although the history of the origin of the use of the concept and meaning of "good" are diverse, the notable discussions of Plato and Aristotle on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leray Spectral Sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. It is usually seen nowadays as a special case of the Grothendieck spectral sequence. Definition Let f:X\to Y be a continuous map of topological spaces, which in particular gives a functor f_* from sheaves of abelian groups on X to sheaves of abelian groups on Y. Composing this with the functor \Gamma of taking sections on \text_\text(Y) is the same as taking sections on \text_\text(X), by the definition of the direct image functor f_*: :\mathrm (X) \xrightarrow \mathrm(Y) \xrightarrow \mathrm. Thus the derived functors of \Gamma \circ f_* compute the sheaf cohomology for X: : R^i (\Gamma \cdot f_*)(\mathcal)=H^i(X,\mathcal). But because f_* and \Gamma send injective objects in \text_\text(X) to \Gamma- acyclic objects in \text_\text(Y), there is a spectral sequencepg 33,19 whose second page is : E^_2=(R^p\Gamma \cdot R^q f_*)(\mathcal)=H^p(Y,R^qf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up to homeomorphism, though usually most classify up to Homotopy#Homotopy equivalence and null-homotopy, homotopy equivalence. Although algebraic topology primarily uses algebra to study topological problems, using topology to solve algebraic problems is sometimes also possible. Algebraic topology, for example, allows for a convenient proof that any subgroup of a free group is again a free group. Main branches of algebraic topology Below are some of the main areas studied in algebraic topology: Homotopy groups In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space. Intuitively, homotopy gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution (algebra)
In mathematics, and more specifically in homological algebra, a resolution (or left resolution; dually a coresolution or right resolution) is an exact sequence of modules (or, more generally, of objects of an abelian category), which is used to define invariants characterizing the structure of a specific module or object of this category. When, as usually, arrows are oriented to the right, the sequence is supposed to be infinite to the left for (left) resolutions, and to the right for right resolutions. However, a finite resolution is one where only finitely many of the objects in the sequence are non-zero; it is usually represented by a finite exact sequence in which the leftmost object (for resolutions) or the rightmost object (for coresolutions) is the zero-object. Generally, the objects in the sequence are restricted to have some property ''P'' (for example to be free). Thus one speaks of a ''P resolution''. In particular, every module has free resolutions, projective resol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leray Cover
In mathematics, a Leray cover(ing) is a cover of a topological space which allows for easy calculation of its cohomology. Such covers are named after Jean Leray. Sheaf cohomology measures the extent to which a locally exact sequence on a fixed topological space, for instance the de Rham sequence, fails to be globally exact. Its definition, using derived functors, is reasonably natural, if technical. Moreover, important properties, such as the existence of a long exact sequence in cohomology corresponding to any short exact sequence of sheaves, follow directly from the definition. However, it is virtually impossible to calculate from the definition. On the other hand, Čech cohomology with respect to an open cover is well-suited to calculation, but of limited usefulness because it depends on the open cover chosen, not only on the sheaves and the space. By taking a direct limit of Čech cohomology over arbitrarily fine covers, we obtain a Čech cohomology theory that does not d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Čech Cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech. Motivation Let ''X'' be a topological space, and let \mathcal be an open cover of ''X''. Let N(\mathcal) denote the nerve of the covering. The idea of Čech cohomology is that, for an open cover \mathcal consisting of sufficiently small open sets, the resulting simplicial complex N(\mathcal) should be a good combinatorial model for the space ''X''. For such a cover, the Čech cohomology of ''X'' is defined to be the simplicial cohomology of the nerve. This idea can be formalized by the notion of a good cover. However, a more general approach is to take the direct limit of the cohomology groups of the nerve over the system of all possible open covers of ''X'', ordered by refinement. This is the approach adopted below. Construction Let ''X'' be a topological space, and l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber Bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a product space B \times F is defined using a continuous surjective map, \pi : E \to B, that in small regions of E behaves just like a projection from corresponding regions of B \times F to B. The map \pi, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber. In the ''trivial'' case, E is just B \times F, and the map \pi is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles, such as the tangent bundle of a mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an Inverse function, invertible Function (mathematics), function that maps one differentiable manifold to another such that both the function and its inverse function, inverse are differentiable. Definition Given two manifolds M and N, a Differentiable manifold#Differentiable functions, differentiable Map (mathematics), map f \colon M \rightarrow N is called a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. They are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a subset X of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)