|
Glossary Of Quantum Computing
This glossary of quantum computing is a list of definitions of terms and concepts used in quantum computing, its sub-disciplines, and related fields. __NOTOC__ References Further reading Textbooks * * * * * * * * * * * * * * * * * * Academic papers * * * * Table 1 lists switching and dephasing times for various systems. * * * * {{Glossaries of science and engineering Models of computation Quantum cryptography Information theory Computational complexity theory Classes of computers Theoretical computer science Open problems Quantum computing A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of wave-particle duality, both particles and waves, and quantum computing takes advantage of this behavior using s ... Wikipedia glossaries using description lists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Computing
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of wave-particle duality, both particles and waves, and quantum computing takes advantage of this behavior using specialized hardware. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations Exponential growth, exponentially faster than any modern "classical" computer. Theoretically a large-scale quantum computer could post-quantum cryptography, break some widely used encryption schemes and aid physicists in performing quantum simulator, physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications. The basic unit of information in quantum computing, the qubit (or "quantum bit"), serves the same function as the bit in classical computing. However, unlike a classical bit, which can be in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Simulators
A simulation is an imitative representation of a process or system that could exist in the real world. In this broad sense, simulation can often be used interchangeably with model. Sometimes a clear distinction between the two terms is made, in which simulations require the use of models; the model represents the key characteristics or behaviors of the selected system or process, whereas the simulation represents the evolution of the model over time. Another way to distinguish between the terms is to define simulation as experimentation with the help of a model. This definition includes time-independent simulations. Often, computer simulation, computers are used to execute the simulation. Simulation is used in many contexts, such as simulation of technology for performance tuning or optimizing, safety engineering, testing, training, education, and video games. Simulation is also used with scientific modelling of natural systems or human systems to gain insight into their functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Emulators
In computing, an emulator is hardware or software that enables one computer system (called the ''host'') to behave like another computer system (called the ''guest''). An emulator typically enables the host system to run software or use peripheral devices designed for the guest system. Emulation refers to the ability of a computer program in an electronic device to emulate (or imitate) another program or device. Many printers, for example, are designed to emulate HP LaserJet printers because a significant amount of software is written specifically for HP models. If a non-HP printer emulates an HP printer, any software designed for an actual HP printer will also function on the non-HP device, producing equivalent print results. Since at least the 1990s, many video game enthusiasts and hobbyists have used emulators to play classic arcade games from the 1980s using the games' original 1980s machine code and data, which is interpreted by a current-era system, and to emulate old ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cloud-based Quantum Computing
Cloud computing, Cloud-based quantum computing refers to the remote access of quantum computing resources—such as quantum emulators, simulators, or processor (computing), processors—via the internet. Cloud access enables users to develop, test, and execute quantum algorithms without the need for direct interaction with specialized hardware, facilitating broader participation in quantum software development and experimentation. In 2016, IBM launched the IBM Quantum Experience, one of the first publicly accessible quantum processors connected to the cloud. In early 2017, researchers at Rigetti Computing demonstrated programmable quantum cloud access through their software platform Forest, which included the Python library. Since the early-2020s, cloud-based quantum computing has grown significantly, with multiple providers offering access to a variety of quantum hardware modalities, including superconducting qubits, trapped ions, neutral atoms, and photonic systems. Major platfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Entropy Of Entanglement
The entropy of entanglement (or entanglement entropy) is a measure of the degree of quantum entanglement between two subsystems constituting a two-part composite quantum system. Given a pure bipartite quantum state of the composite system, it is possible to obtain a reduced density matrix describing knowledge of the state of a subsystem. The entropy of entanglement is the Von Neumann entropy of the reduced density matrix for any of the subsystems. If it is non-zero, it indicates the two subsystems are entangled. More mathematically; if a state describing two subsystems ''A'' and ''B'' , \Psi_\rangle=, \phi_A\rangle, \phi_B\rangle is a separable state, then the reduced density matrix \rho_A=\operatorname_B, \Psi_\rangle\langle\Psi_, =, \phi_A\rangle\langle\phi_A, is a pure state. Thus, the entropy of the state is zero. Similarly, the density matrix of ''B'' would also have 0 entropy. A reduced density matrix having a non-zero entropy is therefore a signal of the existence of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
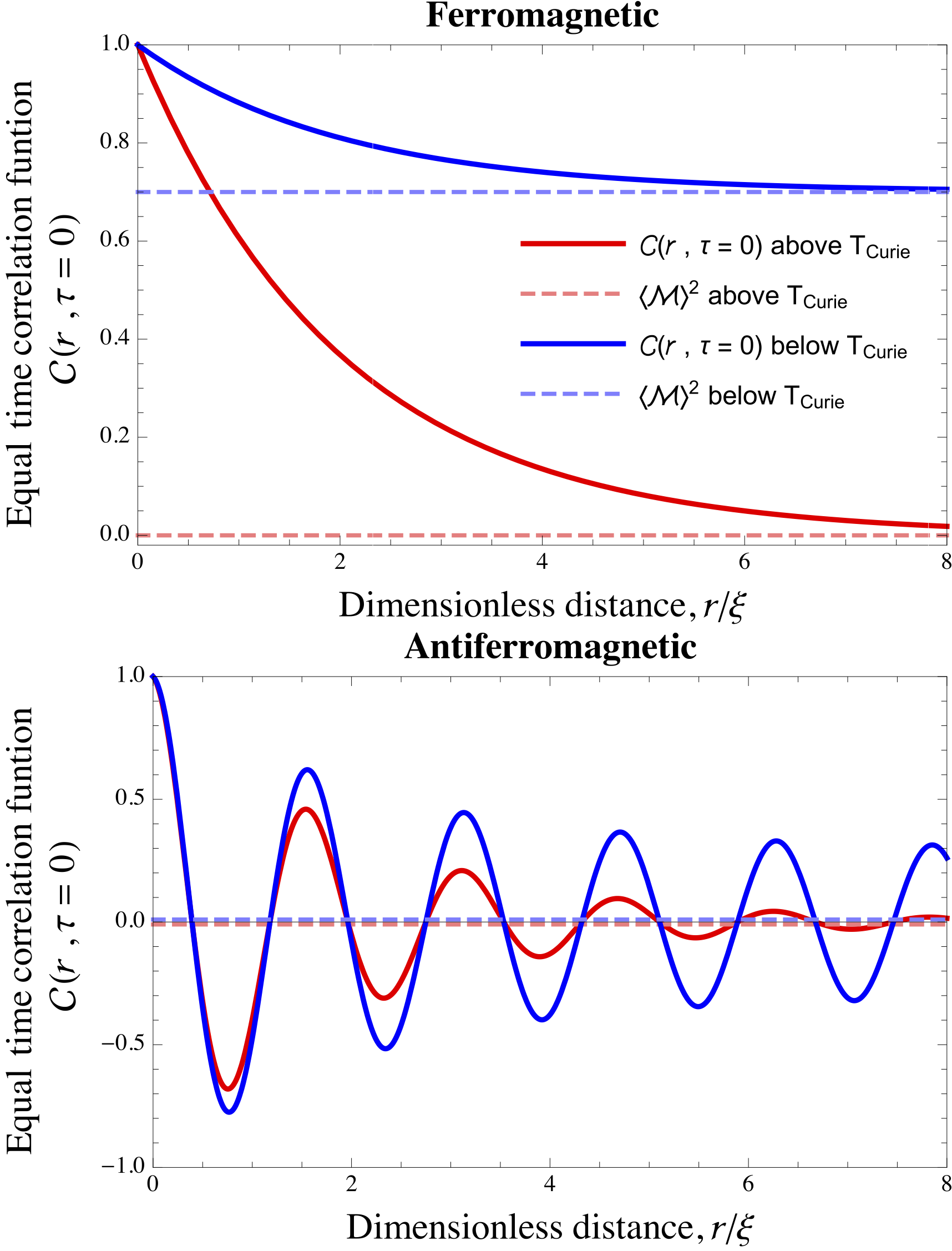
Correlation Function (statistical Mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions or times are related. More specifically, correlation functions measure quantitatively the extent to which microscopic variables fluctuate together, on average, across space and/or time. Keep in mind that correlation doesn’t automatically equate to causation. So, even if there’s a non-zero correlation between two points in space or time, it doesn’t mean there is a direct causal link between them. Sometimes, a correlation can exist without any causal relationship. This could be purely coincidental or due to other underlying factors, known as confounding variables, which cause both points to covary (statistically). A classic example of spatial correlation can be seen in ferromagnetic and antiferromagnetic materials. In these ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fidelity Of Quantum States
In quantum mechanics, notably in quantum information theory, fidelity quantifies the "closeness" between two density matrices. It expresses the probability that one state will pass a test to identify as the other. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space. Definition The fidelity between two quantum states ''\rho'' and ''\sigma'', expressed as density matrices, is commonly defined as:R. Jozsa, ''Fidelity for Mixed Quantum States'', J. Mod. Opt. 41, 2315--2323 (1994). DOI: http://doi.org/10.1080/09500349414552171 :F(\rho, \sigma) = \left(\operatorname \sqrt\right)^2. The square roots in this expression are well-defined because both \rho and \sqrt\rho\sigma\sqrt\rho are positive semidefinite matrices, and the square root of a positive semidefinite matrix is defined via the spectral theorem. The Euclidean inner product from the classical definition is replaced by the Hilbert–Schmidt inner product. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Expectation Value (quantum Mechanics)
In quantum mechanics, the expectation value is the probabilistic expected value of the result (measurement) of an experiment. It can be thought of as an average of all the possible outcomes of a measurement as weighted by their likelihood, and as such it is not the ''most'' probable value of a measurement; indeed the expectation value may have zero probability of occurring (e.g. measurements which can only yield integer values may have a non-integer mean), like the expected value from statistics. It is a fundamental concept in all areas of quantum physics. Operational definition Consider an Operator_(physics), operator A. The expectation value is then \langle A \rangle = \langle \psi , A , \psi \rangle in Bra ket notation, Dirac notation with , \psi \rangle a Normalization (statistics), normalized state vector. Formalism in quantum mechanics In quantum theory, an experimental setup is described by the observable A to be measured, and the Quantum state, state \sigma of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Channel
In quantum information theory, a quantum channel is a communication channel that can transmit quantum information, as well as classical information. An example of quantum information is the general dynamics of a qubit. An example of classical information is a text document transmitted over the Internet. Terminologically, quantum channels are completely positive (CP) trace-preserving maps between spaces of operators. In other words, a quantum channel is just a quantum operation viewed not merely as the reduced dynamics of a system but as a pipeline intended to carry quantum information. (Some authors use the term "quantum operation" to include trace-decreasing maps while reserving "quantum channel" for strictly trace-preserving maps.) Memoryless quantum channel We will assume for the moment that all state spaces of the systems considered, classical or quantum, are finite-dimensional. The memoryless in the section title carries the same meaning as in classical information ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Observable
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum mechanics, observables manifest as self-adjoint operators on a separable complex Hilbert space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Clifford Gates
In quantum computing and quantum information theory, the Clifford gates are the elements of the Clifford group, a set of mathematical transformations which normalize the ''n''-qubit Pauli group, i.e., map tensor products of Pauli matrices to tensor products of Pauli matrices through conjugation. The notion was introduced by Daniel Gottesman and is named after the mathematician William Kingdon Clifford. Quantum circuits that consist of only Clifford gates can be efficiently simulated with a classical computer due to the Gottesman–Knill theorem. The Clifford group is generated by three gates: Hadamard, phase gate ''S'', and CNOT. This set of gates is minimal in the sense that discarding any one gate results in the inability to implement some Clifford operations; removing the Hadamard gate disallows powers of / in the unitary matrix representation, removing the phase gate ''S'' disallows i in the unitary matrix, and removing the CNOT gate reduces the set of implementable ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |