|
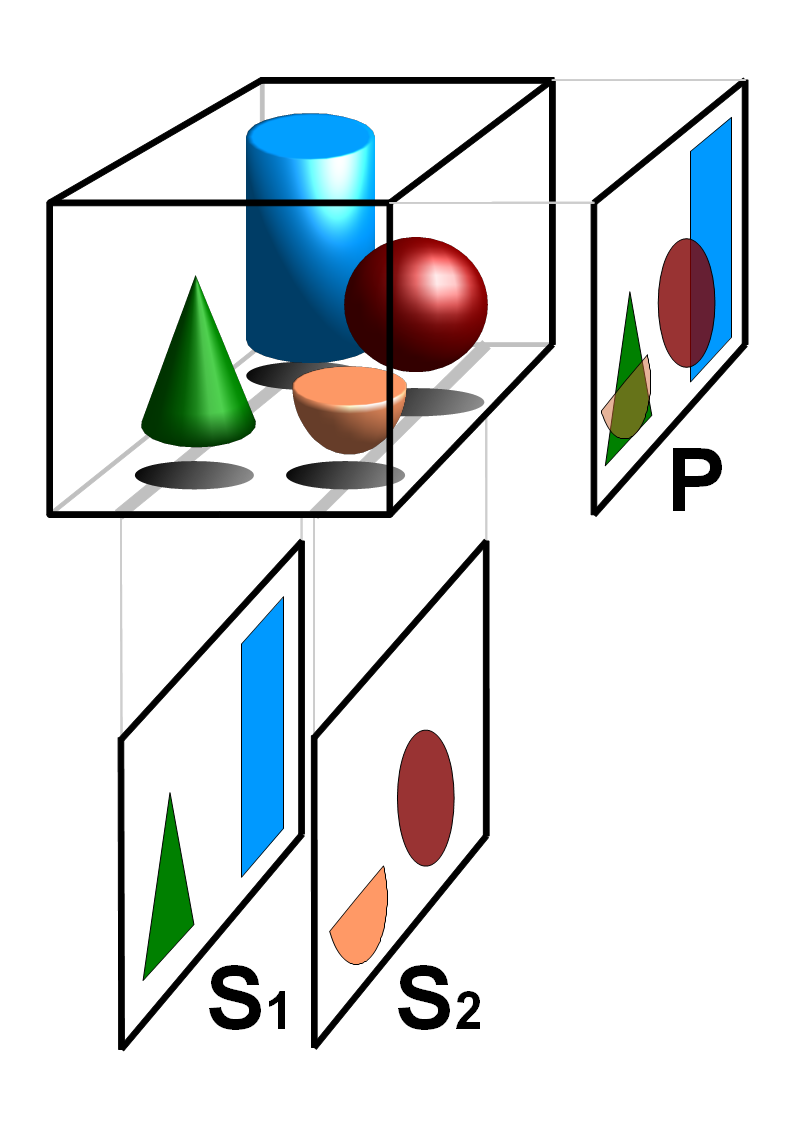
Geometric Tomography
Geometric tomography is a mathematical field that focuses on problems of reconstructing homogeneous (often convex) objects from tomographic data (this might be X-rays, projections, sections, brightness functions, or covariograms). More precisely, according to R.J. Gardner (who introduced the term), "Geometric tomography deals with the retrieval of information about a geometric object from data concerning its projections (shadows) on planes or cross-sections by planes." Gardner, R.J., Geometric Tomography, Cambridge University Press, Cambridge, UK, 2nd ed., 2006 Theory A key theorem in this area states that any convex body in E^n can be determined by parallel, coplanar X-rays in a set of four directions whose slopes have a transcendental cross ratio. Examples * Radon transform * Funk transform (a.k.a. spherical Radon transform) See also *Tomography *Tomographic reconstruction *Discrete tomography *Generalized conic In mathematics, a generalized conic is a geometrical object defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Ratio
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points ''A'', ''B'', ''C'' and ''D'' on a line, their cross ratio is defined as : (A,B;C,D) = \frac where an orientation of the line determines the sign of each distance and the distance is measured as projected into Euclidean space. (If one of the four points is the line's point at infinity, then the two distances involving that point are dropped from the formula.) The point ''D'' is the harmonic conjugate of ''C'' with respect to ''A'' and ''B'' precisely if the cross-ratio of the quadruple is −1, called the ''harmonic ratio''. The cross-ratio can therefore be regarded as measuring the quadruple's deviation from this ratio; hence the name ''anharmonic ratio''. The cross-ratio is preserved by linear fractional transformations. It is essentially the only projective invaria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
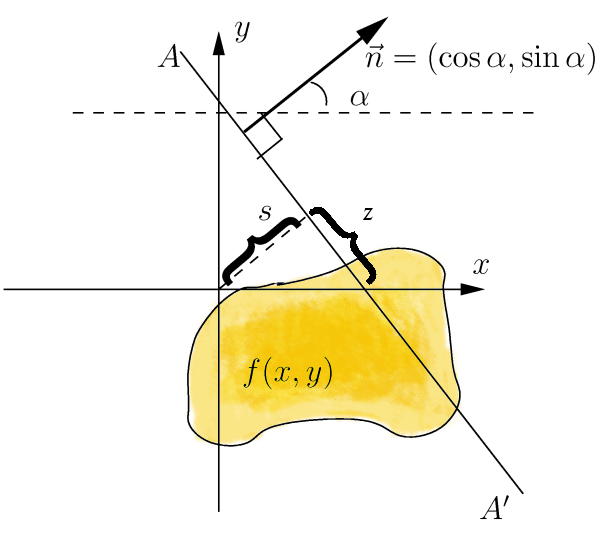
Radon Transform
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object. Explanation If a function f represents an unknown density, then t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Funk Transform
In the mathematical field of integral geometry, the Funk transform (also known as Minkowski–Funk transform, Funk–Radon transform or spherical Radon transform) is an integral transform defined by integrating a function on great circles of the sphere. It was introduced by Paul Funk in 1911, based on the work of . It is closely related to the Radon transform. The original motivation for studying the Funk transform was to describe Zoll metrics on the sphere. Definition The Funk transform is defined as follows. Let ''ƒ'' be a continuous function on the 2-sphere S2 in R3. Then, for a unit vector x, let :Ff(\mathbf) = \int_ f(\mathbf)\,ds(\mathbf) where the integral is carried out with respect to the arclength ''ds'' of the great circle ''C''(x) consisting of all unit vectors perpendicular to x: :C(\mathbf) = \. Inversion The Funk transform annihilates all odd functions, and so it is natural to confine attention to the case when ''ƒ'' is even. In that case, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantum information, and other areas of science. The word ''tomography'' is derived from Ancient Greek τόμος ''tomos'', "slice, section" and γράφω ''graphō'', "to write" or, in this context as well, "to describe." A device used in tomography is called a tomograph, while the image produced is a tomogram. In many cases, the production of these images is based on the mathematical procedure tomographic reconstruction, such as X-ray computed tomography technically being produced from multiple projectional radiographs. Many different reconstruction algorithms exist. Most algorithms fall into one of two categories: filtered back projection (FBP) and iterative reconstruction (IR). These procedures give inexact results: they represent a compr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tomographic Reconstruction
Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security. This article applies in general to reconstruction methods for all kinds of tomography, but some of the terms and physical descriptions refer directly to the reconstruction of X-ray computed tomography. Introducing formula The projection of an object, resulting from the tomographic measurement process at a given angle \theta, is made up of a set of line integrals (see F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
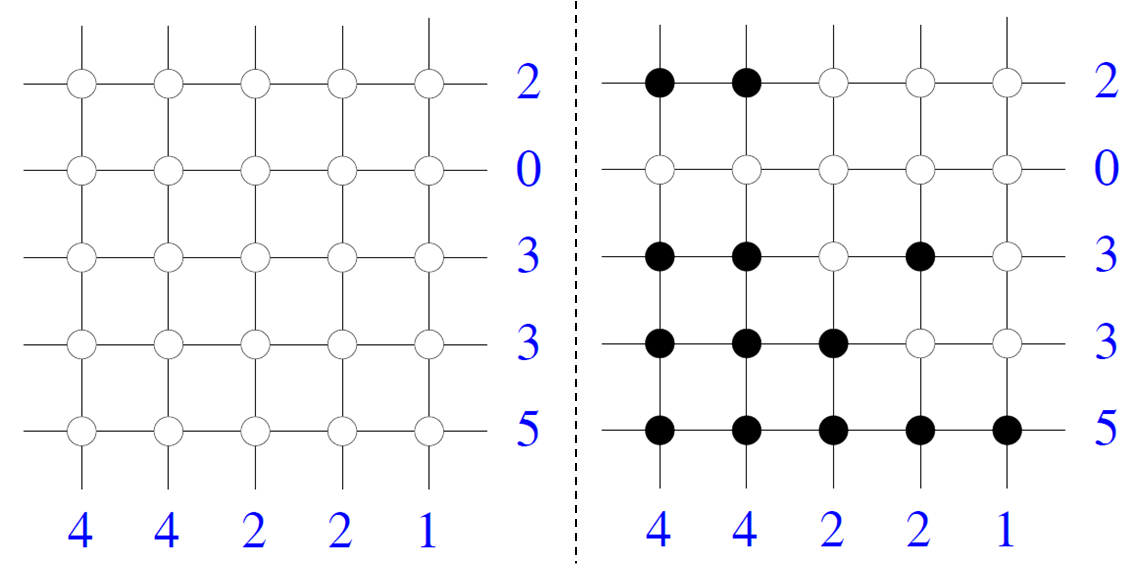
Discrete Tomography
Discrete tomography Herman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007 focuses on the problem of reconstruction of binary images (or finite subsets of the integer lattice) from a small number of their projections. In general, tomography deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a function and the problem posed is to reconstruct this function from its integrals or sums over subsets of its domain. In general, the tomographic inversion problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Conic
In mathematics, a generalized conic is a geometrical object defined by a property which is a generalization of sums defining property of the classical conic. For example, in elementary geometry, an ellipse can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci – in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane is called an ''n''–ellipse and can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates, the equation ''y'' = ''x''2 represents a parabola. The generalized equation ''y'' = ''x'' ''r'', for ''r'' ≠ 0 and ''r'' ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |