|
Greedy Algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time. For example, a greedy strategy for the travelling salesman problem (which is of high computational complexity) is the following heuristic: "At each step of the journey, visit the nearest unvisited city." This heuristic does not intend to find the best solution, but it terminates in a reasonable number of steps; finding an optimal solution to such a complex problem typically requires unreasonably many steps. In mathematical optimization, greedy algorithms optimally solve combinatorial problems having the properties of matroids and give constant-factor approximations to optimization problems with the submodular structure. Specifics Greedy algorith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greedy Algorithm 36 Cents
Greedy may refer to: __NOTOC__ Music * ''Greedy'' (album), a 1997 album by Headless Chickens * "Greedy" (song), a song on the album ''Dangerous Woman'' by Ariana Grande * "Greedy", a single by Canadian rock band Pure * "Greedy", a song on the album ''Mass Nerder'' by the punk rock band All * "Greedy", a song on the album ''Lyfe 268‒192'' by Lyfe Jennings * "Greedy", a song on the album ''Training Day'' by The Away Team * "Greedy", a song on the mixtape ''Keep Flexin'' by Rich the Kid People * Greedy Smith (1956–2019), pseudonym of Andrew McArthur Smith, singer, musician and songwriter with the Australian pop/new wave band Mental As Anything * Greedy Williams (born 1997), American football player nicknamed "Greedy" * Jack Greedy (1929–1988), Canadian racing driver, member of the Canadian Motorsport Hall of Fame Other uses * Greedy algorithm, any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage * ''Greedy'' (film), a 1994 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Cover Problem
The set cover problem is a classical question in combinatorics, computer science, operations research, and complexity theory. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972. Given a set of elements (called the universe) and a collection of sets whose union equals the universe, the set cover problem is to identify the smallest sub-collection of whose union equals the universe. For example, consider the universe and the collection of sets Clearly the union of is . However, we can cover all of the elements with the following, smaller number of sets: More formally, given a universe \mathcal and a family \mathcal of subsets of \mathcal, a ''cover'' is a subfamily \mathcal\subseteq\mathcal of sets whose union is \mathcal. In the set covering decision problem, the input is a pair (\mathcal,\mathcal) and an integer k; the question is whether there is a set covering of size k or less. In the set covering optimization problem, the input is a pair ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ad Hoc Network
An ad hoc network refers to technologies that allow network communications on an ad hoc basis. Associated technologies include: *Wireless ad hoc network *Mobile ad hoc network *Vehicular ad hoc network **Intelligent vehicular ad hoc network * Protocols associated with ad hoc networking **Ad hoc On-Demand Distance Vector Routing **Ad Hoc Configuration Protocol *Smart phone ad hoc network *Ad hoc wireless distribution service Ad hoc Wireless Distribution Service (AWDS) is a layer 2 routing protocol to connect mobile ad hoc networks, sometimes called wireless mesh networks. It is based on a link-state routing protocol, similar to OLSR. Principle of operation AWDS u ... References Computer networking {{networking-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geographic Routing
Geographic routing (also called georouting or position-based routing) is a routing principle that relies on geographic position information. It is mainly proposed for wireless networks and based on the idea that the source sends a message to the geographic location of the destination instead of using the network address. In the area of packet radio networks, the idea of using position information for routing was first proposed in the 1980s for interconnection networks. Geographic routing requires that each node can determine its own location and that the source is aware of the location of the destination. With this information, a message can be routed to the destination without knowledge of the network topology or a prior route discovery. Approaches There are various approaches, such as single-path, multi-path and flooding-based strategies (see for a survey). Most single-path strategies rely on two techniques: greedy forwarding and face routing. Greedy forwarding tries to bring the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Routing
Routing is the process of selecting a path for traffic in a network or between or across multiple networks. Broadly, routing is performed in many types of networks, including circuit-switched networks, such as the public switched telephone network (PSTN), and computer networks, such as the Internet. In packet switching networks, routing is the higher-level decision making that directs network packets from their source toward their destination through intermediate network nodes by specific packet forwarding mechanisms. Packet forwarding is the transit of network packets from one network interface to another. Intermediate nodes are typically network hardware devices such as routers, gateways, firewalls, or switches. General-purpose computers also forward packets and perform routing, although they have no specially optimized hardware for the task. The routing process usually directs forwarding on the basis of routing tables. Routing tables maintain a record of the routes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
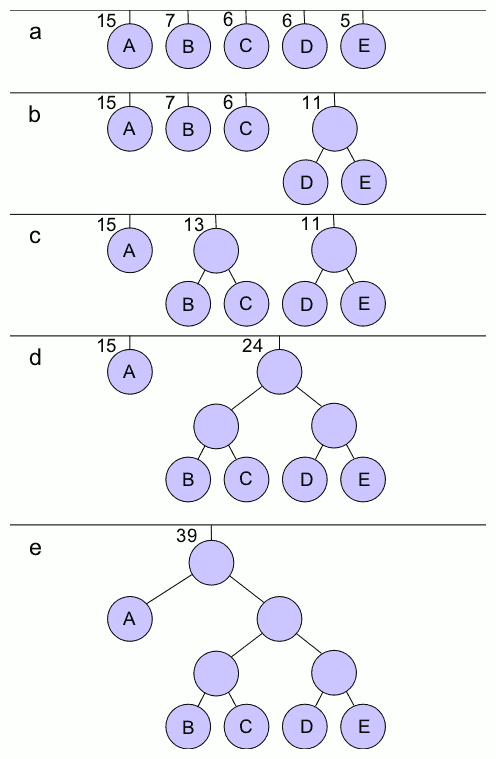
Huffman Tree
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear to the number of input weights if these weights are sorted. However, although o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Spanning Tree
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components. There are many use cases for minimum spanning trees. One example is a telecommunications company trying to lay cable in a new neighborhood. If it is constrained to bury the cable only along certain paths (e.g. roads), then there would be a graph containing the points (e.g. houses) connected by those paths. Some of the paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prim's Algorithm
In computer science, Prim's algorithm (also known as Jarník's algorithm) is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex. The algorithm was developed in 1930 by Czech mathematician Vojtěch Jarník and later rediscovered and republished by computer scientists Robert C. Prim in 1957 and Edsger W. Dijkstra in 1959. Therefore, it is also sometimes called the Jarník's algorithm, Prim–Jarník algorithm, Prim–Dijkstra algorithm. or the DJP algorithm.. Other well-known algorithms for this problem include Kruskal's algorithm and Borůvka's algorithm. These algorithms find the minimum spanning for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kruskal's Algorithm
Kruskal's algorithm finds a minimum spanning forest of an undirected edge-weighted graph. If the graph is connected, it finds a minimum spanning tree. (A minimum spanning tree of a connected graph is a subset of the edges that forms a tree that includes every vertex, where the sum of the weights of all the edges in the tree is minimized. For a disconnected graph, a minimum spanning forest is composed of a minimum spanning tree for each connected component.) It is a greedy algorithm in graph theory as in each step it adds the next lowest-weight edge that will not form a cycle to the minimum spanning forest. This algorithm first appeared in '' Proceedings of the American Mathematical Society'', pp. 48–50 in 1956, and was written by Joseph Kruskal. It was rediscovered by . Other algorithms for this problem include Prim's algorithm, the reverse-delete algorithm, and Borůvka's algorithm. Algorithm * create a forest ''F'' (a set of trees), where each vertex in the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # the problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers to nondeterministic Turing machines, a way of mathematically formalizing the idea of a brute-force search algorithm. Polynomial time refers to an amount of time that is considered "quick" for a det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring Problem
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greedy Coloring
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not in general use the minimum number of colors possible. Different choices of the sequence of vertices will typically produce different colorings of the given graph, so much of the study of greedy colorings has concerned how to find a good ordering. There always exists an ordering that produces an optimal coloring, but although such orderings can be found for many special classes of graphs, they are hard to find in general. Commonly used strategies for vertex ordering involve placing higher-degree vertices earlier than lower-degree vertices, or choosing vertices with fewer available colors in preference to vertices that are less c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |