|
Geomathematics
Geomathematics (also: mathematical geosciences, mathematical geology, mathematical geophysics) is the application of mathematical methods to solve problems in geosciences, including geology and geophysics, and particularly geodynamics and seismology. Applications Geophysical fluid dynamics Geophysical fluid dynamics develops the theory of fluid dynamics for the atmosphere, ocean and Earth's interior. Applications include geodynamics and the theory of the geodynamo. Geophysical inverse theory Geophysical inverse theory is concerned with analyzing geophysical data to get model parameters. It is concerned with the question: What can be known about the Earth's interior from measurements on the surface? Generally there are limits on what can be known even in the ideal limit of exact data. The goal of inverse theory is to determine the spatial distribution of some variable (for example, density or seismic wave velocity). The distribution determines the values of an observable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Dimension
In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a topologically invariant way. Informal discussion For ordinary Euclidean spaces, the Lebesgue covering dimension is just the ordinary Euclidean dimension: zero for points, one for lines, two for planes, and so on. However, not all topological spaces have this kind of "obvious" dimension, and so a precise definition is needed in such cases. The definition proceeds by examining what happens when the space is covered by open sets. In general, a topological space ''X'' can be covered by open sets, in that one can find a collection of open sets such that ''X'' lies inside of their union. The covering dimension is the smallest number ''n'' such that for every cover, there is a refinement in which every point in ''X'' lies in the intersection of no more than ''n'' + 1 covering sets. This is the gist o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earthquakes
An earthquakealso called a quake, tremor, or tembloris the shaking of the Earth's surface resulting from a sudden release of energy in the lithosphere that creates seismic waves. Earthquakes can range in intensity, from those so weak they cannot be felt, to those violent enough to propel objects and people into the air, damage critical infrastructure, and wreak destruction across entire cities. The seismic activity of an area is the frequency, type, and size of earthquakes experienced over a particular time. The seismicity at a particular location in the Earth is the average rate of seismic energy release per unit volume. In its most general sense, the word ''earthquake'' is used to describe any seismic event that generates seismic waves. Earthquakes can occur naturally or be induced by human activities, such as mining, fracking, and nuclear weapons testing. The initial point of rupture is called the hypocenter or focus, while the ground level directly above it is the epi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
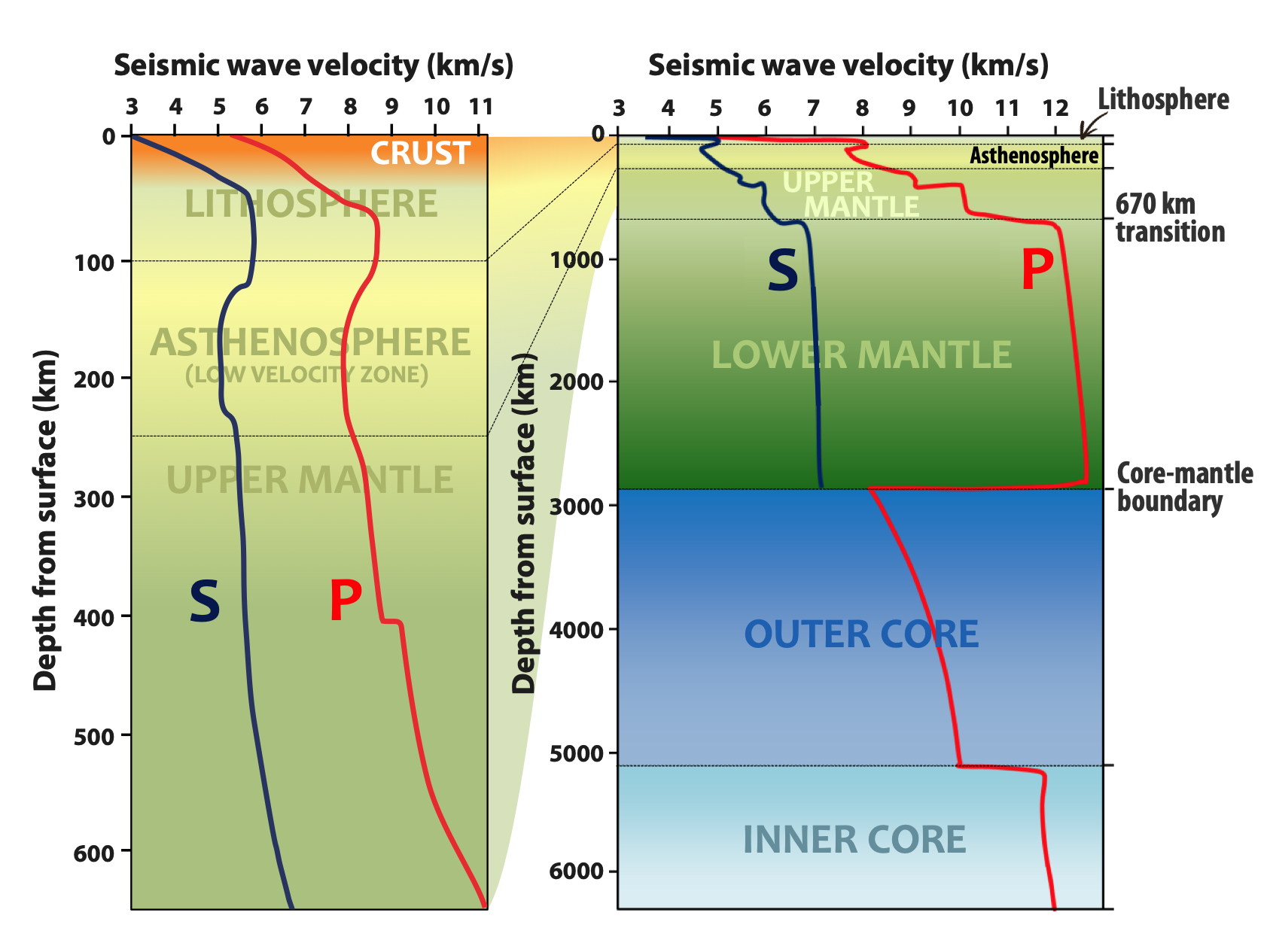
Seismic Waves
A seismic wave is a mechanical wave of acoustic wave, acoustic energy that travels through the Earth or another planetary body. It can result from an earthquake (or generally, a quake (natural phenomenon), quake), types of volcanic eruptions, volcanic eruption, magma movement, a large landslide and a large man-made explosion that produces low-frequency acoustic energy. Seismic waves are studied by seismology, seismologists, who record the waves using seismometers, hydrophones (in water), or accelerometers. Seismic waves are distinguished from seismic noise (ambient vibration), which is persistent low-amplitude vibration arising from a variety of natural and anthropogenic sources. The signal velocity, propagation velocity of a seismic wave depends on density and elasticity (physics), elasticity of the medium as well as the type of wave. Velocity tends to increase with depth through Earth's crust (geology), crust and mantle (geology), mantle, but drops sharply going from the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismic Tomography
Seismic tomography or seismotomography is a technique for imaging the subsurface of the Earth using seismic waves. The properties of seismic waves are modified by the material through which they travel. By comparing the differences in seismic waves recorded at different locations, it is possible to create a model of the subsurface structure. Most commonly, these seismic waves are generated by earthquakes or man-made sources such as explosions. Different types of waves, including P, S, Rayleigh, and Love waves can be used for tomographic images, though each comes with their own benefits and downsides and are used depending on the geologic setting, seismometer coverage, distance from nearby earthquakes, and required resolution. The model created by tomographic imaging is almost always a seismic velocity model, and features within this model may be interpreted as structural, thermal, or compositional variations. Geoscientists apply seismic tomography to a wide variety of settings i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Validation
In statistics, model validation is the task of evaluating whether a chosen statistical model is appropriate or not. Oftentimes in statistical inference, inferences from models that appear to fit their data may be flukes, resulting in a misunderstanding by researchers of the actual relevance of their model. To combat this, model validation is used to test whether a statistical model can hold up to permutations in the data. Model validation is also called model criticism or model evaluation. This topic is not to be confused with the closely related task of model selection, the process of discriminating between multiple candidate models: model validation does not concern so much the conceptual design of models as it tests only the consistency between a chosen model and its stated outputs. There are many ways to validate a model. Residual plots plot the difference between the actual data and the model's predictions: correlations in the residual plots may indicate a flaw in the model. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
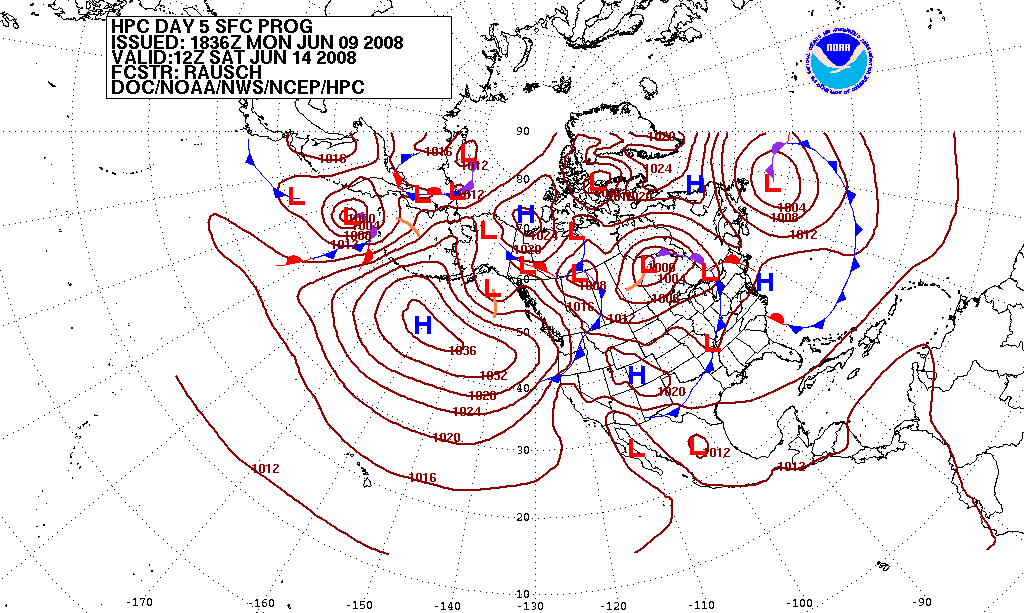
Weather Forecasting
Weather forecasting or weather prediction is the application of science and technology forecasting, to predict the conditions of the Earth's atmosphere, atmosphere for a given location and time. People have attempted to predict the weather informally for thousands of years and formally since the 19th century. Weather forecasts are made by collecting quantitative data about the current state of the atmosphere, land, and ocean and using meteorology to project how the atmosphere will change at a given place. Once calculated manually based mainly upon changes in atmospheric pressure, barometric pressure, current weather conditions, and sky conditions or cloud cover, weather forecasting now relies on numerical weather prediction, computer-based models that take many atmospheric factors into account. Human input is still required to pick the best possible model to base the forecast upon, which involves pattern recognition skills, teleconnections, knowledge of model performance, and kn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Assimilation
Data assimilation refers to a large group of methods that update information from numerical computer models with information from observations. Data assimilation is used to update model states, model trajectories over time, model parameters, and combinations thereof. What distinguishes data assimilation from other estimation methods is that the computer model is a dynamical model, i.e. the model describes how model variables change over time, and its firm mathematical foundation in Bayesian Inference. As such, it generalizes inverse methods and has close connections with machine learning. Data assimilation initially developed in the field of numerical weather prediction. Numerical weather prediction models are equations describing the evolution of the atmosphere, typically coded into a computer program. When these models are used for forecasting the model output quickly deviates from the real atmosphere. Hence, we use observations of the atmosphere to keep the model on track. Data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Sciences
Earth science or geoscience includes all fields of natural science related to the planet Earth. This is a branch of science dealing with the physical, chemical, and biological complex constitutions and synergistic linkages of Earth's four spheres: the biosphere, hydrosphere/ cryosphere, atmosphere, and geosphere (or lithosphere). Earth science can be considered to be a branch of planetary science but with a much older history. Geology Geology is broadly the study of Earth's structure, substance, and processes. Geology is largely the study of the lithosphere, or Earth's surface, including the crust and rocks. It includes the physical characteristics and processes that occur in the lithosphere as well as how they are affected by geothermal energy. It incorporates aspects of chemistry, physics, and biology as elements of geology interact. Historical geology is the application of geology to interpret Earth history and how it has changed over time. Geochemistry studies the che ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractals
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine geometry, affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they Scaling (geometry), scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gabor Korvin
Gabor Korvin (born in 1942 in Hungary) is a Hungarian Mathematician. He served as a professor at the Department of Earth Sciences, King Fahd University of Petroleum and Minerals. His main areas of research interest include fractal geometry in the earth sciences, statistical rock physics and mathematical geophysics. He is a well-known Applied Mathematician, Geophysicist, Petrophysicist, Historian. At KFUPM he was Coordinator of the Reservoir Characterization Research Group. As Professor, he taught Reservoir Characterization, Seismic Stratigraphy, Petrophysics & Well logging, Solid Earth Geophysics, Geoelectric Exploration, Reflection Seismology, Inverse Problems, Geostatistics and Reservoir Characterization. Fractal Models in the Earth Sciences by Gabor Korvin was one of the earlier books on the application of Fractals in the Earth Sciences. Education * Ph.D. in geophysics, Univ. Heavy Industries, Miskolc, Hungary, 1978 * M.Sc. in Applied Mathematics, Univ. Nat. Sciences, Bud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |