|
Genomic Control
Genomic control (GC) is a statistical method that is used to control for the confounding effects of population stratification in genetic association studies. The method was originally outlined by Bernie Devlin and Kathryn Roeder in a 1999 paper. It involves using a set of anonymous genetic markers to estimate the effect of population structure on the distribution of the chi-square statistic. The distribution of the chi-square statistics for a given allele that is suspected to be associated with a given trait can then be compared to the distribution of the same statistics for an allele that is expected not to be related to the trait. The method is supposed to involve the use of markers that are not linked to the marker being tested for a possible association. In theory, it takes advantage of the tendency of population structure to cause overdispersion of test statistics in association analyses. The genomic control method is as robust as family-based designs, despite being appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding
In statistics, a confounder (also confounding variable, confounding factor, extraneous determinant or lurking variable) is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Confounds are threats to internal validity. Definition Confounding is defined in terms of the data generating model. Let ''X'' be some independent variable, and ''Y'' some dependent variable. To estimate the effect of ''X'' on ''Y'', the statistician must suppress the effects of extraneous variables that influence both ''X'' and ''Y''. We say that ''X'' a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Statistics
Robust statistics are statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normal. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but which are not unduly affected by outliers or other small departures from model assumptions. In statistics, classical estimation methods rely heavily on assumptions which are often not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
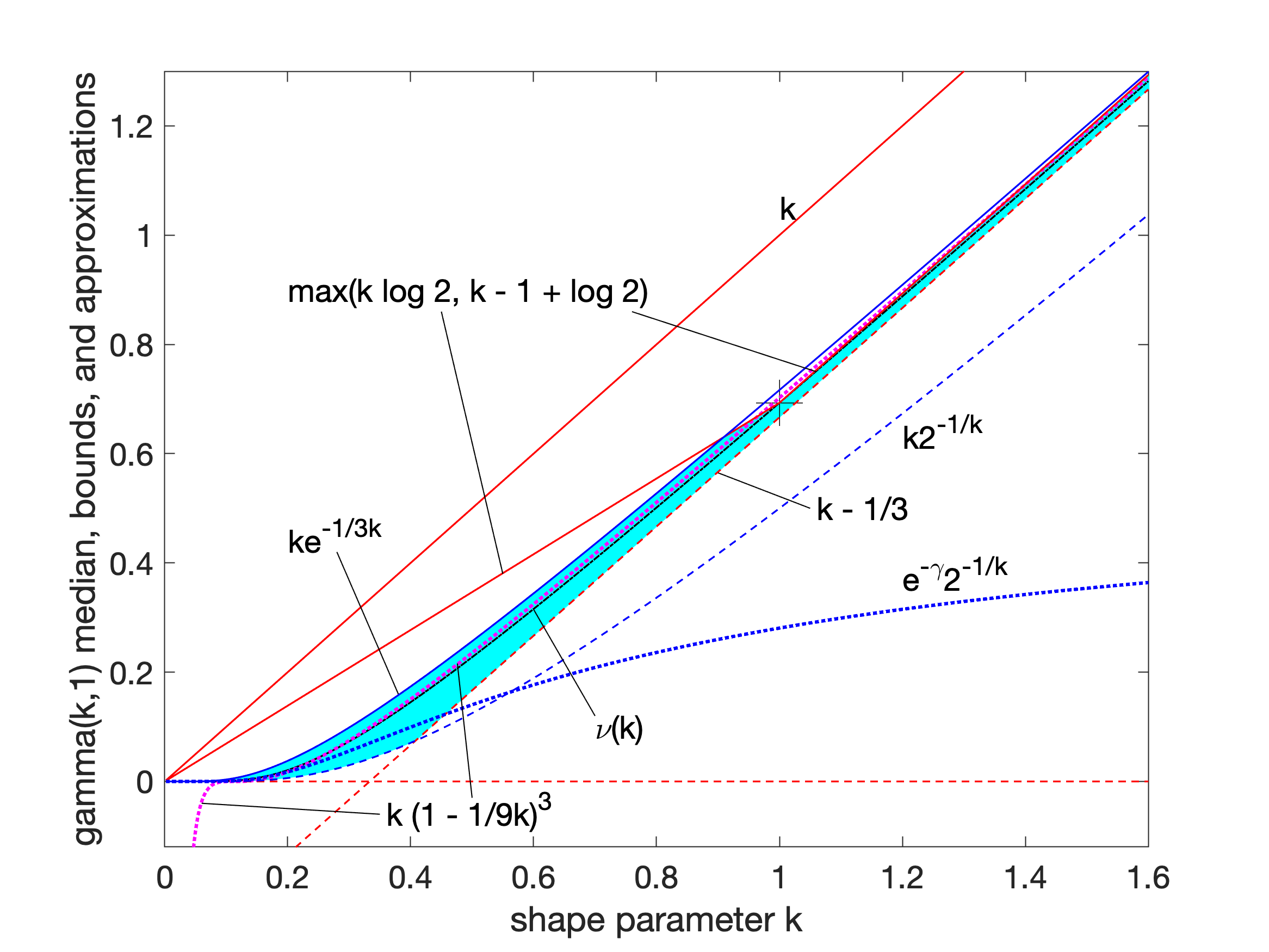
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two- parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient Of Inbreeding
The coefficient of inbreeding of an individual is the probability that two alleles at any locus in an individual are identical by descent from the common ancestor(s) of the two parents. The coefficient of inbreeding is: The probability that two alleles at a given locus are identical by descent. The coefficient of relationship The coefficient of relationship is a measure of the degree of consanguinity (or biological relationship) between two individuals. The term coefficient of relationship was defined by Sewall Wright in 1922, and was derived from his definition of ... is: The proportion of genes that are held in common by two individuals as a result of direct or collateral relationship. References Population genetics {{genetics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
In scientific research, the null hypothesis (often denoted ''H''0) is the claim that no difference or relationship exists between two sets of data or variables being analyzed. The null hypothesis is that any experimentally observed difference is due to chance alone, and an underlying causative relationship does not exist, hence the term "null". In addition to the null hypothesis, an alternative hypothesis is also developed, which claims that a relationship does exist between two variables. Basic definitions The ''null hypothesis'' and the ''alternative hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data. The hypotheses are conjectures about a statistical model of the population, which are based on a sample of the population. The tests are core elements of statistical inference, heavily used in the interpretation of scientific experimental data, to separate scientific claims ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-square Test
A chi-squared test (also chi-square or test) is a statistical hypothesis test used in the analysis of contingency tables when the sample sizes are large. In simpler terms, this test is primarily used to examine whether two categorical variables (''two dimensions of the contingency table'') are independent in influencing the test statistic (''values within the table''). The test is valid when the test statistic is chi-squared distributed under the null hypothesis, specifically Pearson's chi-squared test and variants thereof. Pearson's chi-squared test is used to determine whether there is a statistically significant difference between the expected frequencies and the observed frequencies in one or more categories of a contingency table. For contingency tables with smaller sample sizes, a Fisher's exact test is used instead. In the standard applications of this test, the observations are classified into mutually exclusive classes. If the null hypothesis that there are no differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Candidate Gene
The candidate gene approach to conducting genetic association studies focuses on associations between genetic variation within pre-specified genes of interest, and phenotypes or disease states. This is in contrast to genome-wide association studies (GWAS), which is a hypothesis-free approach that scans the entire genome for associations between common genetic variants (typically SNPs) and traits of interest. Candidate genes are most often selected for study based on ''a priori'' knowledge of the gene's biological functional impact on the trait or disease in question. The rationale behind focusing on allelic variation in specific, biologically relevant regions of the genome is that certain alleles within a gene may directly impact the function of the gene in question and lead to variation in the phenotype or disease state being investigated. This approach often uses the case-control study design to try to answer the question, "Is one allele of a candidate gene more frequently seen in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation that views probability as the limit of the relative frequency of an event after many trials. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can be used to estimate the parameters of a probability distribution or statistical model. Since Bayesian statistics treats pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequentist Statistics
Frequentist inference is a type of statistical inference based in frequentist probability, which treats “probability” in equivalent terms to “frequency” and draws conclusions from sample-data by means of emphasizing the frequency or proportion of findings in the data. Frequentist-inference underlies frequentist statistics, in which the well-established methodologies of statistical hypothesis testing and confidence intervals are founded. History of frequentist statistics The history of frequentist statistics is more recent than its prevailing philosophical rival, Bayesian statistics. Frequentist statistics were largely developed in the early 20th century and have recently developed to become the dominant paradigm in inferential statistics, while Bayesian statistics were invented in the 19th century. Despite this dominance, there is no agreement as to whether frequentism is better than Bayesian statistics, with a vocal minority of professionals studying statistical infe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type I And Type II Errors
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unlu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cochran–Armitage Test For Trend
The Cochran–Armitage test for trend, named for William Cochran and Peter Armitage, is used in categorical data analysis when the aim is to assess for the presence of an association between a variable with two categories and an ordinal variable with ''k'' categories. It modifies the Pearson chi-squared test to incorporate a suspected ordering in the effects of the ''k'' categories of the second variable. For example, doses of a treatment can be ordered as 'low', 'medium', and 'high', and we may suspect that the treatment benefit cannot become smaller as the dose increases. The trend test is often used as a genotype-based test for case-control genetic association studies. Introduction The trend test is applied when the data take the form of a 2 × ''k'' contingency table. For example, if ''k'' = 3 we have This table can be completed with the marginal totals of the two variables where ''R''1 = ''N''11 + ''N''12 + ''N''1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |