|
Formal Equivalence Checking
Formal equivalence checking process is a part of electronic design automation (EDA), commonly used during the development of digital integrated circuits, to formally prove that two representations of a circuit design exhibit exactly the same behavior. Equivalence checking and levels of abstraction In general, there is a wide range of possible definitions of functional equivalence covering comparisons between different levels of abstraction and varying granularity of timing details. *The most common approach is to consider the problem of machine equivalence which defines two synchronous design specifications functionally equivalent if, clock by clock, they produce ''exactly'' the same sequence of output signals for ''any'' valid sequence of input signals. *Microprocessor designers use equivalence checking to compare the functions specified for the instruction set architecture (ISA) with a register transfer level (RTL) implementation, ensuring that any program executed on bot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Design Automation
Electronic design automation (EDA), also referred to as electronic computer-aided design (ECAD), is a category of software tools for designing Electronics, electronic systems such as integrated circuits and printed circuit boards. The tools work together in a Design flow (EDA), design flow that chip designers use to design and analyze entire semiconductor chips. Since a modern semiconductor chip can have billions of components, EDA tools are essential for their design; this article in particular describes EDA specifically with respect to integrated circuits (ICs). History Early days The earliest electronic design automation is attributed to IBM with the documentation of its IBM 700/7000 series, 700 series computers in the 1950s. Prior to the development of EDA, integrated circuits were designed by hand and manually laid out. Some advanced shops used geometric software to generate tapes for a Gerber format, Gerber photoplotter, responsible for generating a monochromatic ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Design For Test
Design for testing or design for testability (DFT) consists of integrated circuit design techniques that add testability features to a hardware product design. The added features make it easier to develop and apply manufacturing tests to the designed hardware. The purpose of manufacturing tests is to validate that the product hardware contains no manufacturing defects that could adversely affect the product's correct functioning. Tests are applied at several steps in the hardware manufacturing flow and, for certain products, may also be used for hardware maintenance in the customer's environment. The tests are generally driven by test programs that execute using automatic test equipment (ATE) or, in the case of system maintenance, inside the assembled system itself. In addition to finding and indicating the presence of defects (i.e., the test fails), tests may be able to log diagnostic information about the nature of the encountered test fails. The diagnostic information can be u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cadence Design Systems
Cadence Design Systems, Inc. (stylized as cādence)Investor's Business DailCEO Lip-Bu Tan Molds Troubled Cadence Into Long-Term LeaderRetrieved November 12, 2020 is an American multinational corporation, multinational technology and computational software company. Headquartered in San Jose, California, Cadence was formed in 1988 through the merger of SDA Systems and ECAD, Inc., ECAD. Initially specialized in Electronic design automation, electronic design automation (EDA) software for the semiconductor industry, currently the company makes software and Electronic hardware, hardware for designing products such as integrated circuits, System on chip, systems on chips (SoCs), printed circuit boards,The StreeHow Cadence Designs the FutureRetrieved July 21, 2020 and pharmaceutical drugs, also licensing intellectual property for the electronics, aerospace, defense and automotive industries, among others. History 1983–1999 Founded in 1983 in San Jose, California, Cadence Design Systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mentor Graphics
Mentor Graphics Corporation was a US-based electronic design automation (EDA) multinational corporation for electrical engineering and electronics, headquartered in Wilsonville, Oregon. Founded in 1981, the company distributed products that assist in electronic design automation, simulation tools for analog mixed-signal design, VPN solutions, and fluid dynamics and heat transfer tools. The company leveraged Apollo Computer workstations to differentiate itself within the computer-aided engineering (CAE) market with its software and hardware. Mentor Graphics was acquired by Siemens in 2017. The name was retired in 2021 and renamed Siemens EDA, a segment of Siemens Digital Industries Software. History Mentor Graphics was founded in 1981 by Tom Bruggere, Gerry Langeler, and Dave Moffenbeier, all formerly of Tektronix. The company raised $55 million in funding through an initial public offering in 1984. Mentor initially wrote software that ran only in Apollo workstation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositional Formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed. If the values of all variables in a propositional formula are given, it determines a unique truth value. A propositional formula may also be called a propositional expression, a sentence, or a sentential formula. A propositional formula is constructed from simple propositions, such as "five is greater than three" or propositional variables such as ''p'' and ''q'', using connectives or logical operators such as NOT, AND, OR, or IMPLIES; for example: : (''p'' AND NOT ''q'') IMPLIES (''p'' OR ''q''). In mathematics, a propositional formula is often more briefly referred to as a "proposition", but, more precisely, a propositional formula is not a proposition but a formal expression that ''denotes'' a proposition, a formal object under discussion, just like an expression such as "" is not a value, but denotes a value. In some contexts, maintaining the distinction may be of importanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Satisfiability Problem
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) asks whether there exists an Interpretation (logic), interpretation that Satisfiability, satisfies a given Boolean logic, Boolean Formula (mathematical logic), formula. In other words, it asks whether the formula's variables can be consistently replaced by the values TRUE or FALSE to make the formula evaluate to TRUE. If this is the case, the formula is called ''satisfiable'', else ''unsatisfiable''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable. SAT is the first problem that was proven to be NP-complete—this is the Cook–Levin theorem. This means that all problems in the complexity class NP (complexity), NP, which includes a wide range of natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
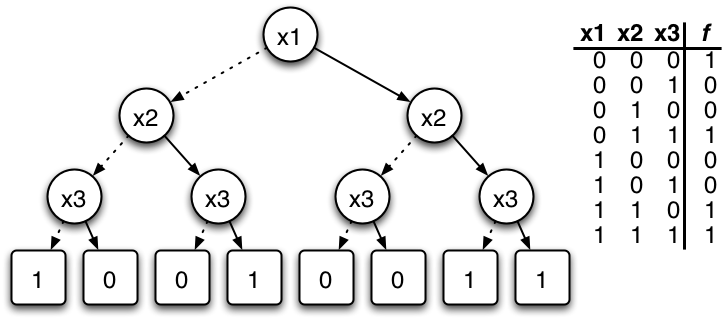
Binary Decision Diagram
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression. Similar data structures include negation normal form (NNF), Zhegalkin polynomials, and propositional directed acyclic graphs (PDAG). Definition A Boolean function can be represented as a rooted, directed, acyclic graph, which consists of several (decision) nodes and two terminal nodes. The two terminal nodes are labeled 0 (FALSE) and 1 (TRUE). Each (decision) node u is labeled by a Boolean variable x_i and has two child nodes called low child and high child. The edge from node u to a low (or high) child represents an assignment of the value FALSE (or TRUE, respectively) to variable x_i. Such a BDD i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics. Formal verification is a key incentive for formal specification of systems, and is at the core of formal methods. It represents an important dimension of analysis and verification in electronic design automation and is one approach to software verification. The use of formal verification enables the highest Evaluation Assurance Level ( EAL7) in the framework of common criteria for computer security certification. Formal verification can be helpful in proving the correctness of systems such as: cryptographic protocols, combinational circuits, digital circuits with internal memory, and software expressed as source code in a programming language. Prominent examples of verified software systems include the CompCert verified C compiler and the seL ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponent
In mathematics, exponentiation, denoted , is an operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_.In particular, b^1=b. The exponent is usually shown as a superscript to the right of the base as or in computer code as b^n. This binary operation is often read as " to the power "; it may also be referred to as " raised to the th power", "the th power of ", or, most briefly, " to the ". The above definition of b^n immediately implies several properties, in particular the multiplication rule:There are three common notations for multiplication: x\times y is most commonly used for explicit numbers and at a very elementary level; xy is most common when variables are used; x\cdot y is used for emphasizing that one talks of multiplication or when omitting the multiplication sign would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic Simulation
Logic simulation is the use of simulation software to predict the behavior of digital circuits and hardware description languages. Simulation can be performed at varying degrees of physical abstraction, such as at the transistor level, gate level, register-transfer level (RTL), electronic system-level (ESL), or behavioral level. Use in verification Logic simulation may be used as part of the verification process in designing hardware. Simulations have the advantage of providing a familiar look and feel to the user in that it is constructed from the same language and symbols used in design. By allowing the user to interact directly with the design, simulation is a natural way for the designer to get feedback on their design. Length of simulation The level of effort required to debug and then verify the design is proportional to the maturity of the design. That is, early in the design's life, bugs and incorrect behavior are usually found quickly. As the design matures, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering Change Order
An engineering change order (ECO), also called an engineering change notice (ECN), engineering change (EC), or engineering release notice (ERN), is an artifact used to implement changes to components or end products. The ECO is utilized to control and coordinate changes to product designs that evolve over time. The need for an engineering change may be triggered by a number of events and varies by industry. Typical engineering change categories are: * Product Evolution - a change resulting in applying an existing part to a new application and maintaining backwards compatibility * Cost Reduction - a change resulting in lower overall cost to produce or maintain * Product Performance - a change that improves the capabilities of the item * Safety - a change required to enhance the safety to those using or interacting with the item Usage and contents An ECO is defined as " document approved by the design activity that describes and authorizes the implementation of an engineerin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Equivalence
In logic and mathematics, statements p and q are said to be logically equivalent if they have the same truth value in every model. The logical equivalence of p and q is sometimes expressed as p \equiv q, p :: q, \textsfpq, or p \iff q, depending on the notation being used. However, these symbols are also used for material equivalence, so proper interpretation would depend on the context. Logical equivalence is different from material equivalence, although the two concepts are intrinsically related. Logical equivalences In logic, many common logical equivalences exist and are often listed as laws or properties. The following tables illustrate some of these. General logical equivalences Logical equivalences involving conditional statements :#p \rightarrow q \equiv \neg p \vee q :#p \rightarrow q \equiv \neg q \rightarrow \neg p :#p \vee q \equiv \neg p \rightarrow q :#p \wedge q \equiv \neg (p \rightarrow \neg q) :#\neg (p \rightarrow q) \equiv p \wedge \neg q :#(p \righta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |