|
Propositional Formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed. If the values of all variables in a propositional formula are given, it determines a unique truth value. A propositional formula may also be called a propositional expression, a sentence, or a sentential formula. A propositional formula is constructed from simple propositions, such as "five is greater than three" or propositional variables such as ''p'' and ''q'', using connectives or logical operators such as NOT, AND, OR, or IMPLIES; for example: : (''p'' AND NOT ''q'') IMPLIES (''p'' OR ''q''). In mathematics, a propositional formula is often more briefly referred to as a "proposition", but, more precisely, a propositional formula is not a proposition but a formal expression that ''denotes'' a proposition, a formal object under discussion, just like an expression such as "" is not a value, but denotes a value. In some contexts, maintaining the distinction may be of importanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositional Logic
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contrast it with System F, but it should not be confused with first-order logic. It deals with propositions (which can be true or false) and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives representing the truth functions of conjunction, disjunction, implication, biconditional, and negation. Some sources include other connectives, as in the table below. Unlike first-order logic, propositional logic does not deal with non-logical objects, predicates about them, or quantifiers. However, all the machinery of propositional logic is included in first-order logic and higher-order logics. In this sense, propositional logi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
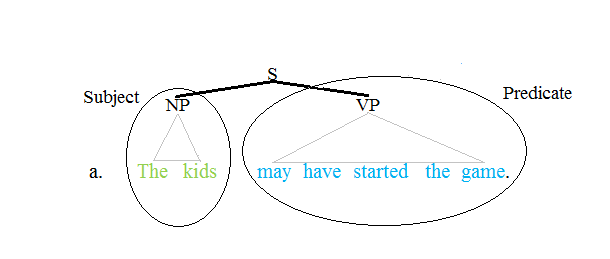
Predicate (grammar)
The term predicate is used in two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject (grammar), subject, and the other defines it as only the main content verb or associated predicative expression of a clause. Thus, by the first definition, the predicate of the sentence ''Frank likes cake'' is ''likes cake'', while by the second definition, it is only the content verb ''likes'', and ''Frank'' and ''cake'' are the argument (linguistics), arguments of this predicate. The conflict between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic Circuits
A logic gate is a device that performs a Boolean function, a logical operation performed on one or more Binary number, binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has, for instance, zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device (see ideal and real op-amps for comparison). The primary way of building logic gates uses diodes or transistors acting as electronic switches. Today, most logic gates are made from MOSFETs (metal–oxide–semiconductor field-effect transistors). ''From Integrated circuit'' They can also be constructed using vacuum tubes, electromagnetic relays with relay logic, fluidic logic, pneumatics#Pneumatic logic, pneumatic logic, optics, molecular logic gate, molecules, acoustics, or even Analytical Engine, mechanical or thermal elements. Logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the constr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Test
The Turing test, originally called the imitation game by Alan Turing in 1949,. Turing wrote about the ‘imitation game’ centrally and extensively throughout his 1950 text, but apparently retired the term thereafter. He referred to ‘ istest’ four times—three times in pp. 446–447 and once on p. 454. He also referred to it as an ‘experiment’—once on p. 436, twice on p. 455, and twice again on p. 457—and used the term ‘viva voce’ (p. 446). See also #Versions, below. Turing gives a more precise version of the question later in the paper: " ese questions reequivalent to this, 'Let us fix our attention on one particular digital computer C. Is it true that by modifying this computer to have an adequate storage, suitably increasing its speed of action, and providing it with an appropriate programme, C can be made to play satisfactorily the part of A in the imitation game, the part of B being taken by a man? is a test of a machine's ability to exhibit intellige ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of research in computer science that develops and studies methods and software that enable machines to machine perception, perceive their environment and use machine learning, learning and intelligence to take actions that maximize their chances of achieving defined goals. High-profile applications of AI include advanced web search engines (e.g., Google Search); recommendation systems (used by YouTube, Amazon (company), Amazon, and Netflix); virtual assistants (e.g., Google Assistant, Siri, and Amazon Alexa, Alexa); autonomous vehicles (e.g., Waymo); Generative artificial intelligence, generative and Computational creativity, creative tools (e.g., ChatGPT and AI art); and Superintelligence, superhuman play and analysis in strategy games (e.g., ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truth Table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid. A truth table has one column for each input variable (for example, A and B), and one final column showing all of the possible results of the logical operation that the table represents (for example, A XOR B). Each row of the truth table contains one possible configuration of the input variables (for instance, A=true, B=false), and the result of the operation for those values. A proposition's truth table is a graphical representation of its truth function. The truth function can be more useful for mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deductive Reasoning
Deductive reasoning is the process of drawing valid inferences. An inference is valid if its conclusion follows logically from its premises, meaning that it is impossible for the premises to be true and the conclusion to be false. For example, the inference from the premises "all men are mortal" and " Socrates is a man" to the conclusion "Socrates is mortal" is deductively valid. An argument is ''sound'' if it is valid ''and'' all its premises are true. One approach defines deduction in terms of the intentions of the author: they have to intend for the premises to offer deductive support to the conclusion. With the help of this modification, it is possible to distinguish valid from invalid deductive reasoning: it is invalid if the author's belief about the deductive support is false, but even invalid deductive reasoning is a form of deductive reasoning. Deductive logic studies under what conditions an argument is valid. According to the semantic approach, an argument is valid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Law
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality x \cdot (y + z) = x \cdot y + x \cdot z is always true in elementary algebra. For example, in elementary arithmetic, one has 2 \cdot (1 + 3) = (2 \cdot 1) + (2 \cdot 3). Therefore, one would say that multiplication ''distributes'' over addition. This basic property of numbers is part of the definition of most algebraic structures that have two operations called addition and multiplication, such as complex numbers, polynomials, matrices, rings, and fields. It is also encountered in Boolean algebra and mathematical logic, where each of the logical and (denoted \,\land\,) and the logical or (denoted \,\lor\,) distributes over the other. Definition Given a set S and two binary operators \,*\, and \,+\, on S, *the operation \,*\, is over (or with respect to) \,+\, if, given any elements x, y, \text z of S, x * (y + z) = (x * y) + (x * z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositional Calculus
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contrast it with System F, but it should not be confused with first-order logic. It deals with propositions (which can be Truth value, true or false) and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives representing the truth functions of Logical conjunction, conjunction, Logical disjunction, disjunction, Material conditional, implication, Logical biconditional, biconditional, and negation. Some sources include other connectives, as in the table below. Unlike first-order logic, propositional logic does not deal with non-logical objects, predicates about them, or Quantifier (logic), quantifiers. However, all the machinery of pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction between sense and reference. Sense is given by the ideas and concepts associated with an expression while reference is the object to which an expression points. Semantics contrasts with syntax, which studies the rules that dictate how to create grammatically correct sentences, and pragmatics, which investigates how people use language in communication. Lexical semantics is the branch of semantics that studies word meaning. It examines whether words have one or several meanings and in what lexical relations they stand to one another. Phrasal semantics studies the meaning of sentences by exploring the phenomenon of compositionality or how new meanings can be created by arranging words. Formal semantics (natural language), Formal semantics relies o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntax
In linguistics, syntax ( ) is the study of how words and morphemes combine to form larger units such as phrases and sentences. Central concerns of syntax include word order, grammatical relations, hierarchical sentence structure (constituency), agreement, the nature of crosslinguistic variation, and the relationship between form and meaning (semantics). Diverse approaches, such as generative grammar and functional grammar, offer unique perspectives on syntax, reflecting its complexity and centrality to understanding human language. Etymology The word ''syntax'' comes from the ancient Greek word , meaning an orderly or systematic arrangement, which consists of (''syn-'', "together" or "alike"), and (''táxis'', "arrangement"). In Hellenistic Greek, this also specifically developed a use referring to the grammatical order of words, with a slightly altered spelling: . The English term, which first appeared in 1548, is partly borrowed from Latin () and Greek, though the L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Quantifier
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first-order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The most commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic: each can be defined in terms of the other using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing has t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |