binary decision diagram on:
[Wikipedia]
[Google]
[Amazon]
In
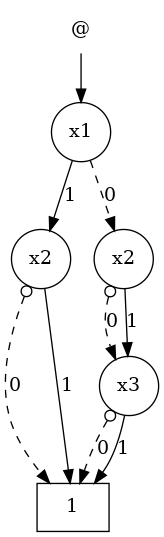 An ROBDD can be represented even more compactly, using complemented edges, also known as ''complement links''. The resulting BDD is sometimes known as a ''typed BDD'' or ''signed BDD''.
Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.
Two advantages of using complemented edges when representing BDDs are:
* computing the negation of a BDD takes constant time
* space usage (i.e., required memory) is reduced (by a factor at most 2)
However, Knuth argues otherwise:
:''Although such links are used by all the major BDD packages, they are hard to recommend because the computer programs become much more complicated. The memory saving is usually negligible, and never better than a factor of 2; furthermore, the author's experiments show little gain in running time.''
A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.
For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.
An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., . Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.
An ROBDD can be represented even more compactly, using complemented edges, also known as ''complement links''. The resulting BDD is sometimes known as a ''typed BDD'' or ''signed BDD''.
Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.
Two advantages of using complemented edges when representing BDDs are:
* computing the negation of a BDD takes constant time
* space usage (i.e., required memory) is reduced (by a factor at most 2)
However, Knuth argues otherwise:
:''Although such links are used by all the major BDD packages, they are hard to recommend because the computer programs become much more complicated. The memory saving is usually negligible, and never better than a factor of 2; furthermore, the author's experiments show little gain in running time.''
A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.
For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.
An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., . Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.
Fun With Binary Decision Diagrams (BDDs)
lecture by
List of BDD software libraries
for several programming languages. Diagrams Graph data structures Model checking Boolean algebra Knowledge compilation {{Diagrams in logic
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, a binary decision diagram (BDD) or branching program is a data structure
In computer science, a data structure is a data organization and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the relationships amo ...
that is used to represent a Boolean function
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually , or ). Alternative names are switching function, used especially in older computer science literature, and truth functi ...
. On a more abstract level, BDDs can be considered as a compressed representation of sets or relation
Relation or relations may refer to:
General uses
* International relations, the study of interconnection of politics, economics, and law on a global level
* Interpersonal relationship, association or acquaintance between two or more people
* ...
s. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.
Similar data structure
In computer science, a data structure is a data organization and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the relationships amo ...
s include negation normal form (NNF), Zhegalkin polynomials, and propositional directed acyclic graphs (PDAG).
Definition
A Boolean function can be represented as a rooted, directed, acyclicgraph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
, which consists of several (decision) nodes and two terminal nodes. The two terminal nodes are labeled 0 (FALSE) and 1 (TRUE). Each (decision) node is labeled by a Boolean variable and has two child nodes called low child and high child. The edge from node to a low (or high) child represents an assignment of the value FALSE (or TRUE, respectively) to variable . Such a BDD is called 'ordered' if different variables appear in the same order on all paths from the root. A BDD is said to be 'reduced' if the following two rules have been applied to its graph:
* Merge any isomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
subgraphs.
* Eliminate any node whose two children are isomorphic.
In popular usage, the term BDD almost always refers to Reduced Ordered Binary Decision Diagram (ROBDD in the literature, used when the ordering and reduction aspects need to be emphasized). The advantage of an ROBDD is that it is canonical (unique up to isomorphism) for a particular function and variable order. This property makes it useful in functional equivalence checking and other operations like functional technology mapping.
A path from the root node to the 1-terminal represents a (possibly partial) variable assignment for which the represented Boolean function is true. As the path descends to a low (or high) child from a node, then that node's variable is assigned to 0 (respectively 1).
Example
The left figure below shows a binary decision ''tree'' (the reduction rules are not applied), and atruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
, each representing the function . In the tree on the left, the value of the function can be determined for a given variable assignment by following a path down the graph to a terminal. In the figures below, dotted lines represent edges to a low child, while solid lines represent edges to a high child. Therefore, to find , begin at x1, traverse down the dotted line to x2 (since x1 has an assignment to 0), then down two solid lines (since x2 and x3 each have an assignment to one). This leads to the terminal 1, which is the value of .
The binary decision ''tree'' of the left figure can be transformed into a binary decision ''diagram'' by maximally reducing it according to the two reduction rules. The resulting BDD is shown in the right figure.
Another notation for writing this Boolean function is .
Complemented edges
 An ROBDD can be represented even more compactly, using complemented edges, also known as ''complement links''. The resulting BDD is sometimes known as a ''typed BDD'' or ''signed BDD''.
Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.
Two advantages of using complemented edges when representing BDDs are:
* computing the negation of a BDD takes constant time
* space usage (i.e., required memory) is reduced (by a factor at most 2)
However, Knuth argues otherwise:
:''Although such links are used by all the major BDD packages, they are hard to recommend because the computer programs become much more complicated. The memory saving is usually negligible, and never better than a factor of 2; furthermore, the author's experiments show little gain in running time.''
A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.
For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.
An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., . Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.
An ROBDD can be represented even more compactly, using complemented edges, also known as ''complement links''. The resulting BDD is sometimes known as a ''typed BDD'' or ''signed BDD''.
Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.
Two advantages of using complemented edges when representing BDDs are:
* computing the negation of a BDD takes constant time
* space usage (i.e., required memory) is reduced (by a factor at most 2)
However, Knuth argues otherwise:
:''Although such links are used by all the major BDD packages, they are hard to recommend because the computer programs become much more complicated. The memory saving is usually negligible, and never better than a factor of 2; furthermore, the author's experiments show little gain in running time.''
A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.
For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.
An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., . Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.
History
The basic idea from which the data structure was created is the Shannon expansion. A switching function is split into two sub-functions (cofactors) by assigning one variable (cf. ''if-then-else normal form''). If such a sub-function is considered as a sub-tree, it can be represented by a '' binary decision tree''. Binary decision diagrams (BDDs) were introduced by C. Y. Lee, and further studied and made known by Sheldon B. Akers and Raymond T. Boute. Independently of these authors, a BDD under the name "canonical bracket form" was realized Yu. V. Mamrukov in a CAD for analysis of speed-independent circuits. The full potential for efficient algorithms based on the data structure was investigated by Randal Bryant atCarnegie Mellon University
Carnegie Mellon University (CMU) is a private research university in Pittsburgh, Pennsylvania, United States. The institution was established in 1900 by Andrew Carnegie as the Carnegie Technical Schools. In 1912, it became the Carnegie Institu ...
: his key extensions were to use a fixed variable ordering (for canonical representation) and shared sub-graphs (for compression). Applying these two concepts results in an efficient data structure and algorithms for the representation of sets and relations. By extending the sharing to several BDDs, i.e. one sub-graph is used by several BDDs, the data structure ''Shared Reduced Ordered Binary Decision Diagram'' is defined. The notion of a BDD is now generally used to refer to that particular data structure.
In his video lecture ''Fun With Binary Decision Diagrams (BDDs)'', Donald Knuth
Donald Ervin Knuth ( ; born January 10, 1938) is an American computer scientist and mathematician. He is a professor emeritus at Stanford University. He is the 1974 recipient of the ACM Turing Award, informally considered the Nobel Prize of comp ...
calls BDDs "one of the only really fundamental data structures that came out in the last twenty-five years" and mentions that Bryant's 1986 paper was for some time one of the most-cited papers in computer science.
Adnan Darwiche and his collaborators have shown that BDDs are one of several normal forms for Boolean functions, each induced by a different combination of requirements. Another important normal form identified by Darwiche is decomposable negation normal form or DNNF.
Applications
BDDs are extensively used in CAD software to synthesize circuits (logic synthesis
In computer engineering, logic synthesis is a process by which an abstract specification of desired circuit behavior, typically at register transfer level (RTL), is turned into a design implementation in terms of logic gates, typically by a co ...
) and in formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics.
Formal ver ...
. There are several lesser known applications of BDD, including fault tree
Fault tree analysis (FTA) is a type of failure analysis in which an undesired state of a system is examined. This analysis method is mainly used in safety engineering and reliability engineering to understand how systems can fail, to identify the ...
analysis, Bayesian reasoning, product configuration, and private information retrieval
In cryptography, a private information retrieval (PIR) protocol is a protocol that allows a user to retrieve an item from a server in possession of a database without revealing which item is retrieved. PIR is a weaker version of 1-out-of-''n'' obl ...
.
Every arbitrary BDD (even if it is not reduced or ordered) can be directly implemented in hardware by replacing each node with a 2 to 1 multiplexer
In electronics, a multiplexer (or mux; spelled sometimes as multiplexor), also known as a data selector, is a device that selects between several Analog signal, analog or Digital signal (electronics), digital input signals and forwards the sel ...
; each multiplexer can be directly implemented by a 4-LUT in a FPGA
A field-programmable gate array (FPGA) is a type of configurable integrated circuit that can be repeatedly programmed after manufacturing. FPGAs are a subset of logic devices referred to as programmable logic devices (PLDs). They consist of a ...
. It is not so simple to convert from an arbitrary network of logic gates to a BDD (unlike the and-inverter graph).
BDDs have been applied in efficient Datalog
Datalog is a declarative logic programming language. While it is syntactically a subset of Prolog, Datalog generally uses a bottom-up rather than top-down evaluation model. This difference yields significantly different behavior and properties ...
interpreters.
Variable ordering
The size of the BDD is determined both by the function being represented and by the chosen ordering of the variables. There exist Boolean functions for which depending upon the ordering of the variables we would end up getting a graph whose number of nodes would be linear (in ''n'') at best and exponential at worst (e.g., a ripple carry adder). Consider the Boolean function Using the variable ordering , the BDD needs nodes to represent the function. Using the ordering , the BDD consists of nodes. It is of crucial importance to care about variable ordering when applying this data structure in practice. The problem of finding the best variable ordering isNP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
. For any constant ''c'' > 1 it is even NP-hard to compute a variable ordering resulting in an OBDD with a size that is at most ''c'' times larger than an optimal one. However, there exist efficient heuristics to tackle the problem.
There are functions for which the graph size is always exponential—independent of variable ordering. This holds e.g. for the multiplication function. In fact, the function computing the middle bit of the product of two -bit numbers does not have an OBDD smaller than vertices. (If the multiplication function had polynomial-size OBDDs, it would show that integer factorization
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a comp ...
is in P/poly, which is not known to be true.)
Another notorious example is the hidden weight bit function, regarded as the simplest function with an exponential-sized BDD.
Researchers have suggested refinements on the BDD data structure giving way to a number of related graphs, such as BMD ( binary moment diagrams), ZDD ( zero-suppressed decision diagrams), FBDD ( free binary decision diagrams), FDD ( functional decision diagrams), PDD ( parity decision diagrams), and MTBDDs (multiple terminal BDDs).
Logical operations on BDDs
Many logical operations on BDDs can be implemented bypolynomial-time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations p ...
graph manipulation algorithms:
* conjunction
* disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is ...
* negation
In logic, negation, also called the logical not or logical complement, is an operation (mathematics), operation that takes a Proposition (mathematics), proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \over ...
However, repeating these operations several times, for example forming the conjunction or disjunction of a set of BDDs, may in the worst case result in an exponentially big BDD. This is because any of the preceding operations for two BDDs may result in a BDD with a size proportional to the product of the BDDs' sizes, and consequently for several BDDs the size may be exponential in the number of operations. Variable ordering needs to be considered afresh; what may be a good ordering for (some of) the set of BDDs may not be a good ordering for the result of the operation. Also, since constructing the BDD of a Boolean function solves the NP-complete Boolean satisfiability problem
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) asks whether there exists an Interpretation (logic), interpretation that Satisf ...
and the co-NP-complete tautology problem, constructing the BDD can take exponential time in the size of the Boolean formula even when the resulting BDD is small.
Computing existential abstraction over multiple variables of reduced BDDs is NP-complete.
Model-counting, counting the number of satisfying assignments of a Boolean formula, can be done in polynomial time for BDDs. For general propositional formulas the problem is ♯P
In computational complexity theory, the complexity class #P (pronounced "sharp P" or, sometimes "number P" or "hash P") is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of f ...
-complete and the best known algorithms require an exponential time in the worst case.
See also
*Boolean satisfiability problem
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) asks whether there exists an Interpretation (logic), interpretation that Satisf ...
, the canonical NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''.
Somewhat more precisely, a problem is NP-complete when:
# It is a decision problem, meaning that for any ...
computational problem
In theoretical computer science, a computational problem is one that asks for a solution in terms of an algorithm. For example, the problem of factoring
:"Given a positive integer ''n'', find a nontrivial prime factor of ''n''."
is a computati ...
* L/poly, a complexity class
In computational complexity theory, a complexity class is a set (mathematics), set of computational problems "of related resource-based computational complexity, complexity". The two most commonly analyzed resources are time complexity, time and s ...
that strictly contains the set of problems with polynomially sized BDDs
* Model checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software syst ...
* Radix tree
In computer science, a radix tree (also radix trie or compact prefix tree or compressed trie) is a data structure that represents a space-optimized trie (prefix tree) in which each node that is the only child is merged with its parent. The resu ...
* Barrington's theorem
* Hardware acceleration
Hardware acceleration is the use of computer hardware designed to perform specific functions more efficiently when compared to software running on a general-purpose central processing unit (CPU). Any transformation of data that can be calcula ...
* Karnaugh map
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of ...
, a method of simplifying Boolean algebra expressions
* Zero-suppressed decision diagram
* Algebraic decision diagram, a generalization of BDDs from two-element to arbitrary finite sets
* Sentential Decision Diagram, a generalization of OBDDs
* Influence diagram
An influence diagram (ID) (also called a relevance diagram, decision diagram or a decision network) is a compact graphical and mathematical representation of a decision situation. It is a generalization of a Bayesian network, in which not only ...
References
Further reading
* * Complete textbook available for download. * *External links
Fun With Binary Decision Diagrams (BDDs)
lecture by
Donald Knuth
Donald Ervin Knuth ( ; born January 10, 1938) is an American computer scientist and mathematician. He is a professor emeritus at Stanford University. He is the 1974 recipient of the ACM Turing Award, informally considered the Nobel Prize of comp ...
List of BDD software libraries
for several programming languages. Diagrams Graph data structures Model checking Boolean algebra Knowledge compilation {{Diagrams in logic