|
Froude Number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as: \mathrm = \frac where is the local flow velocity, is the local external field, and is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations. However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water. Origins In open channel flows, introduced first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century. Explanation A continuum model assumes that the substance of the object fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. These models can be used to derive differential equations that describe the behavior of such objects using physical laws, such as mass conservation, momentum conservation, and energy conservation, and some information about the material is provided by constitutive relationships. Continuum mechanics deals with the physical properties of solids and fluids which are independent of any particular coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrodynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity Of Earth
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation). It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm g=\, \mathit\, . In SI units this acceleration is expressed in metres per second squared (in symbols, m/ s2 or m·s−2) or equivalently in newtons per kilogram (N/kg or N·kg−1). Near Earth's surface, the gravity acceleration is approximately , which means that, ignoring the effects of air resistance, the speed of an object falling freely will increase by about per second every second. This quantity is sometimes referred to informally as ''little '' (in contrast, the gravitational constant is referred to as ''big ''). The precise strength of Earth's gravity varies depending on location. The nominal "average" value at Earth's surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
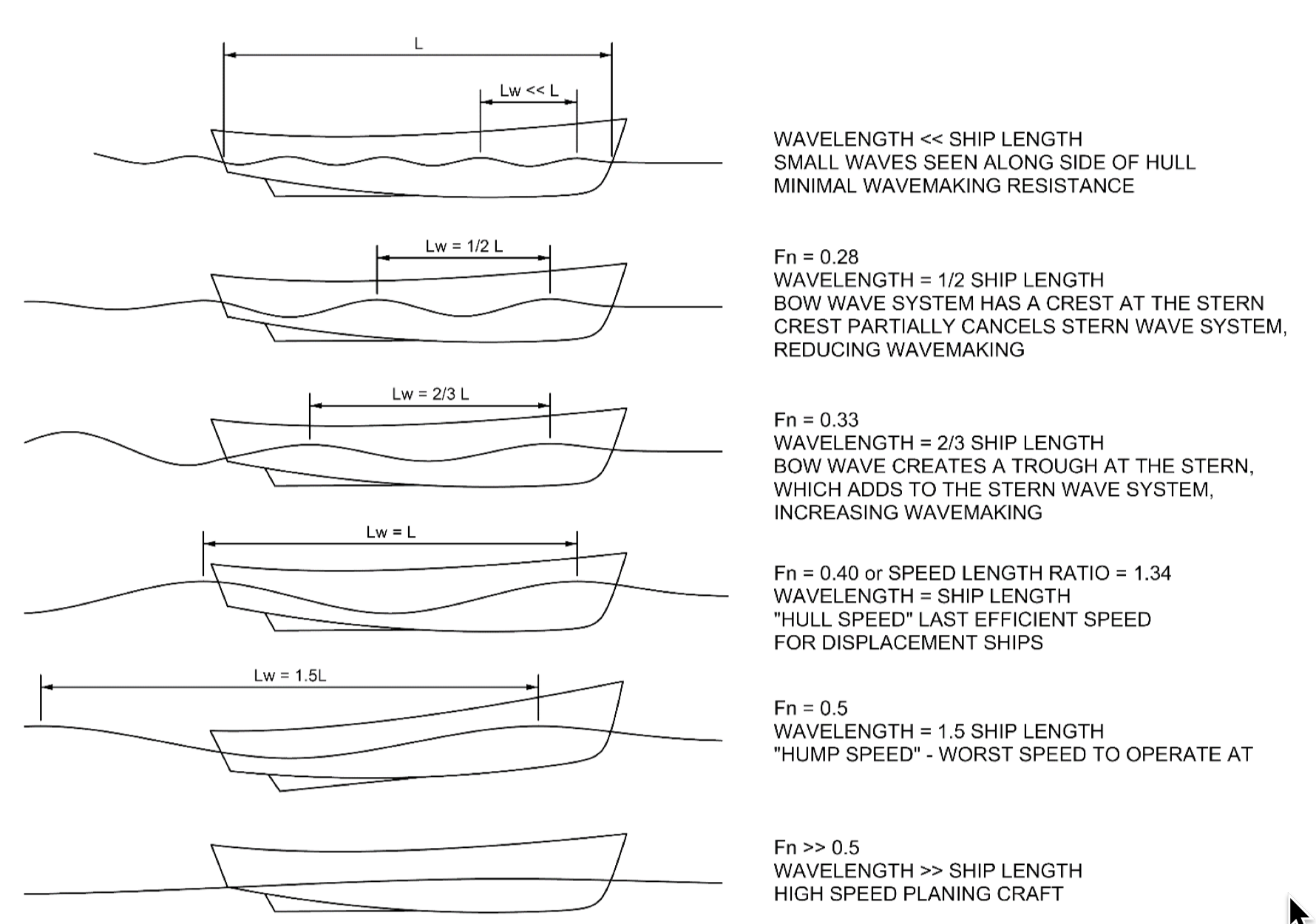
Froude Numbers And Waves
{{disambig ...
Froude (, ) may refer to: * Christine Froude (born 1947), Archdeacon of Malmesbury and Acting Archdeacon of Bristol * Derek Froude (1959– ), New Zealand athlete * Fred Froude (1910–?), Australian rules footballer * Hurrell Froude (1803–1836), Anglican priest * James Anthony Froude (1818–1894), British historian * William Froude (1810–1879), British engineer and hydrodynamicist See also * Froude, Saskatchewan - a small community in Canada * Froude number In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipative System
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter. A tornado may be thought of as a dissipative system. Dissipative systems stand in contrast to conservative systems. A dissipative structure is a dissipative system that has a dynamical regime that is in some sense in a reproducible steady state. This reproducible steady state may be reached by natural evolution of the system, by artifice, or by a combination of these two. Overview A dissipative structure is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. Examples in everyday life include convection, turbulent flow, cyclones, hurricanes and living organisms. Less common examples include lasers, Bénard cells, droplet cluster, and the Belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes' Law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. Stokes' law is derived by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.Batchelor (1967), p. 233. Statement of the law The force of viscosity on a small sphere moving through a viscous fluid is given by: :F_ = 6 \pi \mu R v where: * ''F''d is the frictional force – known as Stokes' drag – acting on the interface between the fluid and the particle * ''μ'' is the dynamic viscosity (some authors use the symbol ''η'') * ''R'' is the radius of the spherical object * ''v'' is the flow velocity relative to the object. In SI units, ''F''d is given in newtons (= kg m s−2), ''μ'' in Pa·s (= kg m−1 s−1), ''R'' in meters, and ''v'' in m/s. Stokes' law makes the following assumptions for the behavior of a particle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal Law
Pascal's law (also Pascal's principle or the principle of transmission of fluid-pressure) is a principle in fluid mechanics given by Blaise Pascal that states that a pressure change at any point in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere. The law was established by French mathematician Blaise Pascal in 1653 and published in 1663. Definition Pascal's principle is defined as This principle is stated mathematically as: : \Delta p =\rho g \cdot\Delta h\, : is the hydrostatic pressure (given in pascals in the SI system), or the difference in pressure at two points within a fluid column, due to the weight of the fluid); :ρ is the fluid density (in kilograms per cubic meter in the SI system); :g is acceleration due to gravity (normally using the sea level acceleration due to Earth's gravity, in meters per second squared); : is the height of fluid above the point of measurement, or the difference in el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes Flow
Stokes flow (named after George Gabriel Stokes), also named creeping flow or creeping motion,Kim, S. & Karrila, S. J. (2005) ''Microhydrodynamics: Principles and Selected Applications'', Dover. . is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. \mathrm \ll 1. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms, sperm and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally. The equations of motion for Stokes flow, called the Stokes equations, are a linearization of the Navier–Stokes equations, and thus can be solved by a number of well-known methods for linear differential equations. The primary Green' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advection Equation
In the field of physics, engineering, and earth sciences, advection is the transport of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is also a fluid. The properties that are carried with the advected substance are conserved properties such as energy. An example of advection is the transport of pollutants or silt in a river by bulk water flow downstream. Another commonly advected quantity is energy or enthalpy. Here the fluid may be any material that contains thermal energy, such as water or air. In general, any substance or conserved, extensive quantity can be advected by a fluid that can hold or contain the quantity or substance. During advection, a fluid transports some conserved quantity or material via bulk motion. The fluid's motion is described mathematically as a vector field, and the transported material is described by a scalar field showing its distribution ov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |