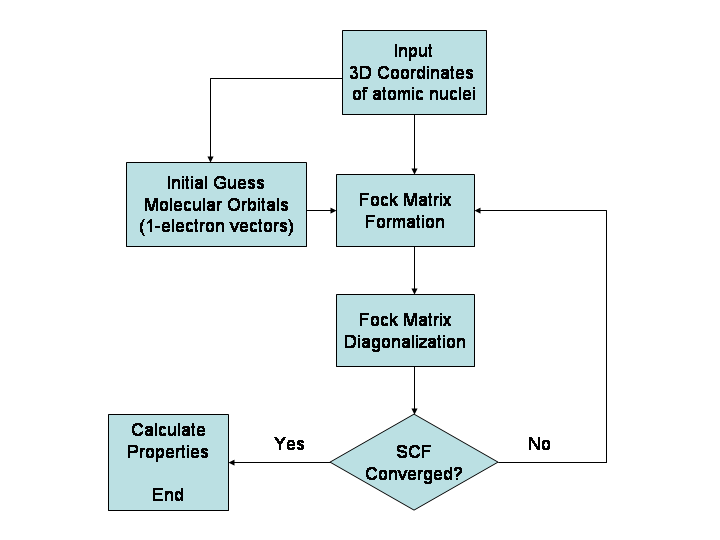
|
Fock Operator
In the Hartree–Fock method of quantum mechanics, the Fock matrix is a matrix approximating the single-electron energy operator of a given quantum system in a given set of basis vectors. It is most often formed in computational chemistry when attempting to solve the Roothaan equations for an atomic or molecular system. The Fock matrix is actually an approximation to the true Hamiltonian operator of the quantum system. It includes the effects of electron-electron repulsion only in an average way. Because the Fock operator is a one-electron operator, it does not include the electron correlation energy. The Fock matrix is defined by the Fock operator. For the restricted case which assumes closed-shell orbitals and single- determinantal wavefunctions, the Fock operator for the ''i''-th electron is given by:Levine, I.N. (1991) ''Quantum Chemistry'' (4th ed., Prentice-Hall), p.403 :\hat F(i) = \hat h(i)+\sum_^ \hat J_j(i)-\hat K_j(i)/math> where: :\hat F(i) is the Fock opera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. Atomic and molecular systems Within the Hartree–Fock method of quantum chemistry, the antisymmetric wave function is approximated by a single Slater determinant. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation within the Born–Oppenheimer approximation. Therefore, the Hartree–Fock limit is always above this exact energy. The difference is called the ''correlation energy'', a term coined by Löwdin. The concept of the correlation energy was studied earlier by Wigner. A certain amount of electron cor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic, Molecular, And Optical Physics
Atomic, molecular, and optical physics (AMO) is the study of matter-matter and light-matter interactions; at the scale of one or a few atoms and energy scales around several electron volts. The three areas are closely interrelated. AMO theory includes classical, semi-classical and quantum treatments. Typically, the theory and applications of emission, absorption, scattering of electromagnetic radiation (light) from excited atoms and molecules, analysis of spectroscopy, generation of lasers and masers, and the optical properties of matter in general, fall into these categories. Atomic and molecular physics Atomic physics is the subfield of AMO that studies atoms as an isolated system of electrons and an atomic nucleus, while molecular physics is the study of the physical properties of molecules. The term ''atomic physics'' is often associated with nuclear power and nuclear bombs, due to the synonymous use of ''atomic'' and ''nuclear'' in standard English. However, physi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Restricted Open-shell Hartree–Fock
Restricted open-shell Hartree–Fock (ROHF) is a variant of Hartree–Fock method for open shell molecules. It uses doubly occupied molecular orbitals as far as possible and then singly occupied orbitals for the unpaired electrons. This is the simple picture for open shell molecules but it is difficult to implement. The foundations of the ROHF method were first formulated by Clemens C. J. Roothaan in a celebrated paper and then extended by various authors, see e.g. for in-depth discussions. As with restricted Hartree–Fock theory for closed shell molecules, it leads to Roothaan equations written in the form of a generalized eigenvalue problem :\mathbf \mathbf = \mathbf \mathbf \mathbf Where F is the so-called Fock matrix (which is a function of C), C is a matrix of coefficients, S is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. Unlike restricted Hartree–Fock theory for closed shell molecules, the form of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unrestricted Hartree–Fock
Unrestricted Hartree–Fock (UHF) theory is the most common molecular orbital method for open shell molecules where the number of electrons of each spin are not equal. While restricted Hartree–Fock theory uses a single molecular orbital twice, one multiplied by the α spin function and the other multiplied by the β spin function in the Slater determinant, unrestricted Hartree–Fock theory uses different molecular orbitals for the α and β electrons. This has been called a ''different orbitals for different spins'' (DODS) method. The result is a pair of coupled Roothaan equations, known as the Pople–Nesbet–Berthier equations. :\mathbf^\alpha\ \mathbf^\alpha\ = \mathbf \mathbf^\alpha\ \mathbf^\alpha\ :\mathbf^\beta\ \mathbf^\beta\ = \mathbf \mathbf^\beta\ \mathbf^\beta\ Where \mathbf^\alpha\ and \mathbf^\beta\ are the Fock matrices for the \alpha\ and \beta\ orbitals, \mathbf^\alpha\ and \mathbf^\beta\ are the matrices of coefficients for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Operator
In quantum mechanics, the exchange operator \hat, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles described by the joint position quantum state \left, x_1, x_2\right\rangle. Since the particles are identical, the notion of exchange symmetry requires that the exchange operator be unitary. Construction In three or higher dimensions, the exchange operator can represent a literal exchange of the positions of the pair of particles by motion of the particles in an adiabatic process, with all other particles held fixed. Such motion is often not carried out in practice. Rather, the operation is treated as a "what if" similar to a parity inversion or time reversal operation. Consider two repeated operations of such a particle exchange: :\hat^2\left, x_1, x_2\right\rangle = \hat\left, x_2, x_1\right\rangle = \left, x_1, x_2\right\rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Operator
The Coulomb operator, named after Charles-Augustin de Coulomb, is a quantum mechanics, quantum mechanical operator (mathematics), operator used in the field of quantum chemistry. Specifically, it is a term found in the Hartree–Fock, Fock operator. It is defined as: \widehat J_j (1) f_i(1)= f_i(1) \int ^2 \frac\,dr_2 where \widehat J_j (1) is the one-electron Coulomb operator defining the repulsion resulting from electron ''j'', f_i(1) is the one-electron wavefunction of the i^ electron being acted upon by the Coulomb operator, \varphi_j(1) is the one-electron wavefunction of the j^ electron, r_ is the distance between electrons (i) and (j) . See also *Core Hamiltonian *Exchange operator References Quantum chemistry Theoretical chemistry Computational chemistry {{quantum-chemistry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term ''atomic orbital'' may also refer to the physical region or space where the electron can be calculated to be present, as predicted by the particular mathematical form of the orbital. Each orbital in an atom is characterized by a set of values of the three quantum numbers , , and , which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (magnetic quantum number). Alternative to the magnetic quantum number, the orbitals are often labeled by the associated harmonic polynomials (e.g., ''xy'', ). Each such orbital can be occupied by a maximum of two electrons, each with its own projection of spin m_s. The simple names s orbital, p orb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-shell
In atomic physics and quantum chemistry, the electron configuration is the distribution of electrons of an atom or molecule (or other physical structure) in atomic or molecular orbitals. For example, the electron configuration of the neon atom is , meaning that the 1s, 2s and 2p subshells are occupied by 2, 2 and 6 electrons respectively. Electronic configurations describe each electron as moving independently in an orbital, in an average field created by all other orbitals. Mathematically, configurations are described by Slater determinants or configuration state functions. According to the laws of quantum mechanics, for systems with only one electron, a level of energy is associated with each electron configuration and in certain conditions, electrons are able to move from one configuration to another by the emission or absorption of a quantum of energy, in the form of a photon. Knowledge of the electron configuration of different atoms is useful in understanding the structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Force
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is conventionally called ''electrostatic force'' or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb, hence the name. Coulomb's law was essential to the development of the theory of electromagnetism, maybe even its starting point, as it made it possible to discuss the quantity of electric charge in a meaningful way. The law states that the magnitude of the electrostatic force of attraction or repulsion between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them. Coulomb studied the repulsive force between bodies having electrical charges of the same sign: Coulomb also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
