|
Excosecant
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astronomy, and spherical trigonometry and could help improve accuracy, but are rarely used today except to simplify some calculations. Exsecant The exsecant, (Latin: ''secans exterior'') also known as exterior, external, outward or outer secant and abbreviated as exsec or exs, is a trigonometric function defined in terms of the secant function sec(''θ''): \operatorname(\theta) = \sec(\theta) - 1 = \frac - 1. The name ''exsecant'' can be understood from a graphical construction of the various trigonometric functions from a unit circle, such as was used historically. sec(''θ'') is the secant line , and the exsecant is the portion of this secant that lies ''exterior'' to the circle (''ex'' is Latin for ''out of''). Excosecant A rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exsecant And Excosecant Plot
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astronomy, and spherical trigonometry and could help improve accuracy, but are rarely used today except to simplify some calculations. Exsecant The exsecant, (Latin: ''secans exterior'') also known as exterior, external, outward or outer secant and abbreviated as exsec or exs, is a trigonometric function defined in terms of the secant function sec(''θ''): \operatorname(\theta) = \sec(\theta) - 1 = \frac - 1. The name ''exsecant'' can be understood from a graphical construction of the various trigonometric functions from a unit circle, such as was used historically. sec(''θ'') is the secant line , and the exsecant is the portion of this secant that lies ''exterior'' to the circle (''ex'' is Latin for ''out of''). Excosecant A rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
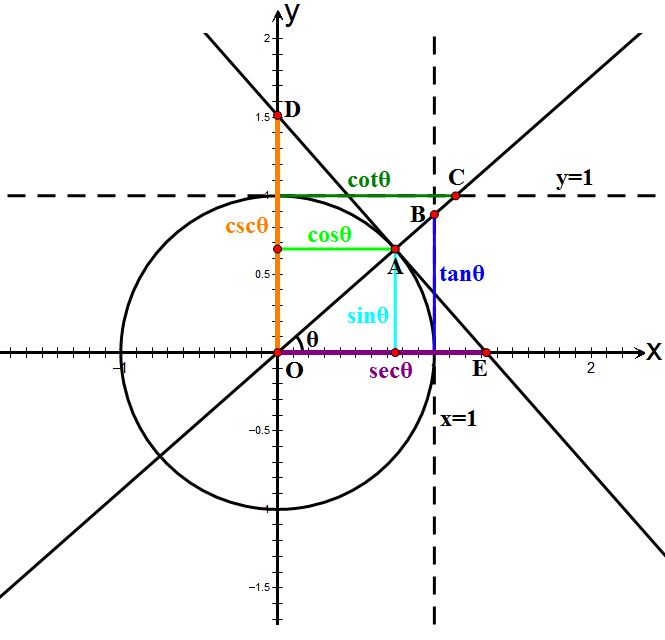
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent (trigonometry)
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Versine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit Āryabhaṭa's sine table , ''Aryabhatia'', Section I) trigonometric tables. The versine of an angle is 1 minus its cosine. There are several related functions, most notably the coversine and haversine. The latter, half a versine, is of particular importance in the haversine formula of navigation. Overview The versine or versed sine is a trigonometric function already appearing in some of ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant (trigonometry)
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cotangent
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosecant
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion methods, and the use of numerical methods. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system's Lagrangian which includes a derivative with respect to time. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2. In relativistic mechanics, this is a good approximation only when ''v'' is much less than the speed of light. The standard unit of kinetic energy is the joule, while the English unit of kinetic energy is the foot-pound. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
