|
Exchange Operator
In quantum mechanics, the exchange operator \hat, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles described by the joint position quantum state \left, x_1, x_2\right\rangle. Since the particles are identical, the notion of exchange symmetry requires that the exchange operator be unitary. Construction In three or higher dimensions, the exchange operator can represent a literal exchange of the positions of the pair of particles by motion of the particles in an adiabatic process, with all other particles held fixed. Such motion is often not carried out in practice. Rather, the operation is treated as a "what if" similar to a parity inversion or time reversal operation. Consider two repeated operations of such a particle exchange: :\hat\left, x_1, x_2\right\rangle = \left, x_2, x_1\right\rangle :\hat^2\left, x_1, x_2\right\rangle = \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–statistics Theorem
The spin–statistics theorem proves that the observed relationship between the intrinsic spin of a particle (angular momentum not due to the orbital motion) and the quantum particle statistics of collections of such particles is a consequence of the mathematics of quantum mechanics. According to the theorem, the many-body wave function for elementary particles with integer spin ( bosons) is symmetric under the exchange of any two particles, whereas for particles with half-integer spin ( fermions), the wave function is antisymmetric under such an exchange. A consequence of the theorem is that non-interacting particles with integer spin obey Bose–Einstein statistics, while those with half-integer spin obey Fermi–Dirac statistics. Background The statistics of indistinguishable particles is among the most fundamental of physical effects. The Pauli exclusion principle that every occupied quantum state contains at most one fermion controls the formation of matter. The basic bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Operator
The Coulomb operator, named after Charles-Augustin de Coulomb, is a quantum mechanical operator used in the field of quantum chemistry. Specifically, it is a term found in the Fock operator. It is defined as: : \widehat J_j (1) f_i(1)= f_i(1) \int ^2 \frac\,dr_2 where : \widehat J_j (1) is the one-electron Coulomb operator defining the repulsion resulting from electron ''j'', : f_i(1) is the one-electron wavefunction of the i^ electron being acted upon by the Coulomb operator, : \varphi_j(2) is the one-electron wavefunction of the j^ electron, : r_ is the distance between electrons (i) and (j) . See also * Core Hamiltonian * Exchange operator In quantum mechanics, the exchange operator \hat, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles descri ... References {{DEFAULTSORT:Coulomb Operator Quantum chemis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Interaction
In chemistry and physics, the exchange interaction is a quantum mechanical constraint on the states of indistinguishable particles. While sometimes called an exchange force, or, in the case of fermions, Pauli repulsion, its consequences cannot always be predicted based on classical ideas of force. Both bosons and fermions can experience the exchange interaction. The wave function of identical particles, indistinguishable particles is subject to exchange symmetry: the wave function either changes sign (for fermions) or remains unchanged (for bosons) when two particles are exchanged. The exchange symmetry alters the Expectation value (quantum mechanics), expectation value of the distance between two indistinguishable particles when their wave functions overlap. For fermions the expectation value of the distance increases, and for bosons it decreases (compared to distinguishable particles). The exchange interaction arises from the combination of exchange symmetry and the Coulomb's l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Interaction
In chemistry and physics, the exchange interaction is a quantum mechanical constraint on the states of indistinguishable particles. While sometimes called an exchange force, or, in the case of fermions, Pauli repulsion, its consequences cannot always be predicted based on classical ideas of force. Both bosons and fermions can experience the exchange interaction. The wave function of identical particles, indistinguishable particles is subject to exchange symmetry: the wave function either changes sign (for fermions) or remains unchanged (for bosons) when two particles are exchanged. The exchange symmetry alters the Expectation value (quantum mechanics), expectation value of the distance between two indistinguishable particles when their wave functions overlap. For fermions the expectation value of the distance increases, and for bosons it decreases (compared to distinguishable particles). The exchange interaction arises from the combination of exchange symmetry and the Coulomb's l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and Thermodynamics, thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
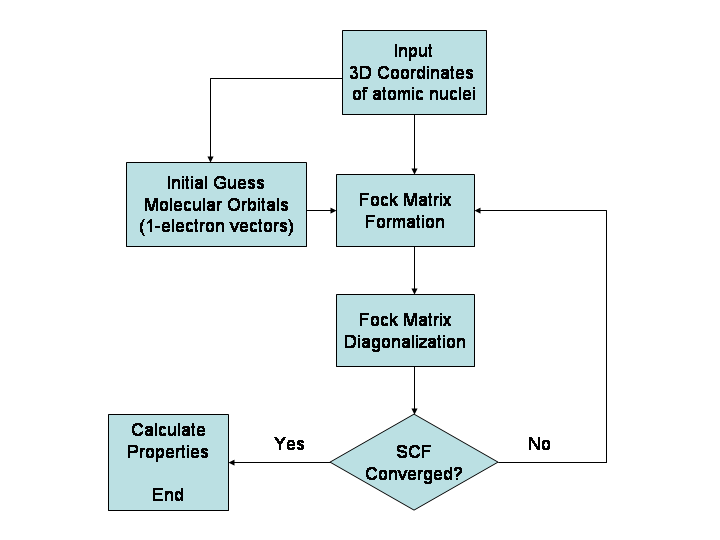
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anyon
In physics, an anyon is a type of quasiparticle so far observed only in two-dimensional physical system, systems. In three-dimensional systems, only two kinds of elementary particles are seen: fermions and bosons. Anyons have statistical properties intermediate between fermions and bosons. In general, the operation of exchange symmetry, exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as ''abelian'' or ''non-abelian''. Abelian anyons, detected by two experiments in 2020, play a major role in the fractional quantum Hall effect. Introduction The statistical mechanics of large many-body systems obeys laws described by Maxwell–Boltzmann statistics. Quantum statistics is more complicated because of the different behaviors of two different kinds of particles called fermions and bosons. In two-dimensional systems, however, there is a third type of particle, called an anyon. In a two-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antisymmetrizer
In quantum mechanics, an antisymmetrizer \mathcal (also known as an antisymmetrizing operatorP.A.M. Dirac, ''The Principles of Quantum Mechanics'', 4th edition, Clarendon, Oxford UK, (1958) p. 248) is a linear operator that makes a wave function of ''N'' identical fermions antisymmetric under the exchange of the coordinates of any pair of fermions. After application of \mathcal the wave function satisfies the Pauli exclusion principle. Since \mathcal is a projection operator, application of the antisymmetrizer to a wave function that is already totally antisymmetric has no effect, acting as the identity operator. Mathematical definition Consider a wave function depending on the space and spin coordinates of ''N'' fermions: : \Psi(1,2, \ldots, N)\quad\text \quad i \leftrightarrow (\mathbf_i, \sigma_i), where the position vector r''i'' of particle ''i'' is a vector in \mathbb^3 and σi takes on 2''s''+1 values, where ''s'' is the half-integral intrinsic spin of the fermion. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conserved Quantity
A conserved quantity is a property or value that remains constant over time in a system even when changes occur in the system. In mathematics, a conserved quantity of a dynamical system is formally defined as a function of the dependent variables, the value of which remains constant along each trajectory of the system. Not all systems have conserved quantities, and conserved quantities are not unique, since one can always produce another such quantity by applying a suitable function, such as adding a constant, to a conserved quantity. Since many laws of physics express some kind of conservation, conserved quantities commonly exist in mathematical models of physical systems. For example, any classical mechanics model will have mechanical energy as a conserved quantity as long as the forces involved are conservative. Differential equations For a first order system of differential equations :\frac = \mathbf f(\mathbf r, t) where bold indicates vector quantities, a scala ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |