|
Evidence Lower Bound
In variational Bayesian methods, the evidence lower bound (often abbreviated ELBO, also sometimes called the variational lower bound or negative variational free energy) is a useful lower bound on the log-likelihood of some observed data. Terminology and notation Let X and Z be random variables, jointly-distributed with distribution p_\theta. For example, p_\theta( X) is the marginal distribution of X, and p_\theta( Z \mid X) is the conditional distribution of Z given X. Then, for any sample x\sim p_\theta, and any distribution q_\phi , we have\ln p_\theta(x) \ge \mathbb \mathbb E_\left \ln\frac \rightThe left-hand side is called the ''evidence'' for x, and the right-hand side is called the ''evidence lower bound for x'', or ''ELBO''. We refer to the above inequality as the ''ELBO inequality''. In the terminology of variational Bayesian methods, the distribution p_\theta( X) is called the ''evidence''. Some authors use the term ''evidence'' to mean \ln p_\theta( X), an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Bayesian Methods
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Measure
In probability theory, an empirical measure is a random measure arising from a particular realization of a (usually finite) sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics. The motivation for studying empirical measures is that it is often impossible to know the true underlying probability measure P. We collect observations X_1, X_2, \dots , X_n and compute relative frequencies. We can estimate P, or a related distribution function F by means of the empirical measure or empirical distribution function, respectively. These are uniformly good estimates under certain conditions. Theorems in the area of empirical processes provide rates of this convergence. Definition Let X_1, X_2, \dots be a sequence of independent identically distributed random variables with values in the state space ''S'' with probability distribution ''P''. Definition :The ''empirical measure'' ''P''''n'' is defined for mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unbiased Estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In statistics, "bias" is an property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased; see bias versus consistency for more. All else being equal, an unbiased estimator is preferable to a biased estimator, although in practice, biased estimators (with generally small bias) are frequently used. When a biased estimator is used, bounds of the bias are calculated. A biased estimator may be used for various reasons: because an unbiased estimator does not exist without further assumptions about a population; because an estimator is difficult to compute (as in unbiased estimation of standard deviation); because a biased esti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Method
In statistics, the delta method is a result concerning the approximate probability distribution for a function of an asymptotically normal statistical estimator from knowledge of the limiting variance of that estimator. History The delta method was derived from propagation of error, and the idea behind was known in the early 19th century. Its statistical application can be traced as far back as 1928 by T. L. Kelley. A formal description of the method was presented by J. L. Doob in 1935. Robert Dorfman also described a version of it in 1938. Univariate delta method While the delta method generalizes easily to a multivariate setting, careful motivation of the technique is more easily demonstrated in univariate terms. Roughly, if there is a sequence of random variables satisfying :, where ''θ'' and ''σ''2 are finite valued constants and \xrightarrow denotes convergence in distribution, then : for any function ''g'' satisfying the property that exists and is non-zero va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations. Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Importance Sampling
Importance sampling is a Monte Carlo method for evaluating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest. Its introduction in statistics is generally attributed to a paper by Teun Kloek and Herman K. van Dijk in 1978, but its precursors can be found in statistical physics as early as 1949. Importance sampling is also related to umbrella sampling in computational physics. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both. Basic theory Let X\colon \Omega\to \mathbb be a random variable in some probability space (\Omega,\mathcal,P). We wish to estimate the expected value of ''X'' under ''P'', denoted E 'X;P'' If we have statistically independent random samples x_1, \ldots, x_n, generated according to ''P'', then an empirical estimate of E 'X;P''is : \widehat_ ;P= \frac \sum_^n x_i \quad \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Integration
In mathematics, Monte Carlo integration is a technique for numerical integration using random numbers. It is a particular Monte Carlo method that numerically computes a definite integral. While other algorithms usually evaluate the integrand at a regular grid, Monte Carlo randomly chooses points at which the integrand is evaluated. This method is particularly useful for higher-dimensional integrals. There are different methods to perform a Monte Carlo integration, such as uniform sampling, stratified sampling, importance sampling, sequential Monte Carlo (also known as a particle filter), and mean-field particle methods. Overview In numerical integration, methods such as the trapezoidal rule use a deterministic approach. Monte Carlo integration, on the other hand, employs a non-deterministic approach: each realization provides a different outcome. In Monte Carlo, the final outcome is an approximation of the correct value with respective error bars, and the correct value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how one probability distribution ''P'' is different from a second, reference probability distribution ''Q''. A simple interpretation of the KL divergence of ''P'' from ''Q'' is the expected excess surprise from using ''Q'' as a model when the actual distribution is ''P''. While it is a distance, it is not a metric, the most familiar type of distance: it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain classes of distributions (notably an exponential family), it satisfies a generalized Pythagorean theorem (which applies to squared distances). In the simple case, a relative entropy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Random Variable
In probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose value is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value. The individual variables in a random vector are grouped together because they are all part of a single mathematical system — often they represent different properties of an individual statistical unit. For example, while a given person has a specific age, height and weight, the representation of these features of ''an unspecified person'' from within a group would be a random vector. Normally each element of a random vector is a real number. Random vectors are often used as the underlying implementation of various types of aggregate random variables, e.g. a random matrix, random tree, random sequence, stochastic process, etc. More formally, a multivariate random variable is a column vector \mathbf = (X_1,\dots,X_n)^\mathsf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayes' Theorem
In probability theory and statistics, Bayes' theorem (alternatively Bayes' law or Bayes' rule), named after Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole. One of the many applications of Bayes' theorem is Bayesian inference, a particular approach to statistical inference. When applied, the probabilities involved in the theorem may have different probability interpretations. With Bayesian probability interpretation, the theorem expresses how a degree of belief, expressed as a probability, should rationally change to account for the availability of related evidence. Bayesian inference is fundamental to Baye ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
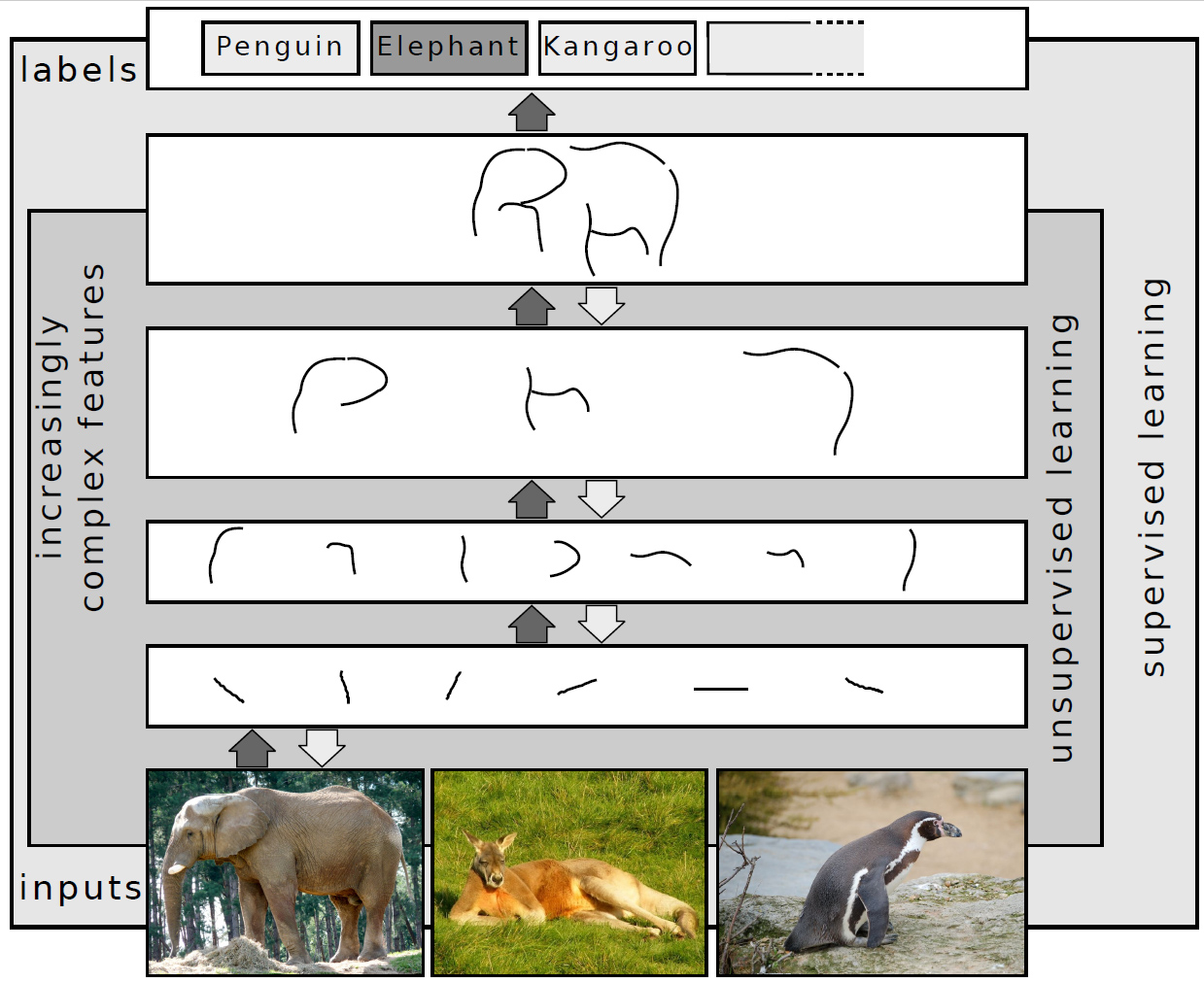
Deep Neural Network
Deep learning (also known as deep structured learning) is part of a broader family of machine learning methods based on artificial neural networks with representation learning. Learning can be supervised, semi-supervised or unsupervised. Deep-learning architectures such as deep neural networks, deep belief networks, deep reinforcement learning, recurrent neural networks, convolutional neural networks and Transformers have been applied to fields including computer vision, speech recognition, natural language processing, machine translation, bioinformatics, drug design, medical image analysis, climate science, material inspection and board game programs, where they have produced results comparable to and in some cases surpassing human expert performance. Artificial neural networks (ANNs) were inspired by information processing and distributed communication nodes in biological systems. ANNs have various differences from biological brains. Specifically, artificial neural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |