|
Euler's Function
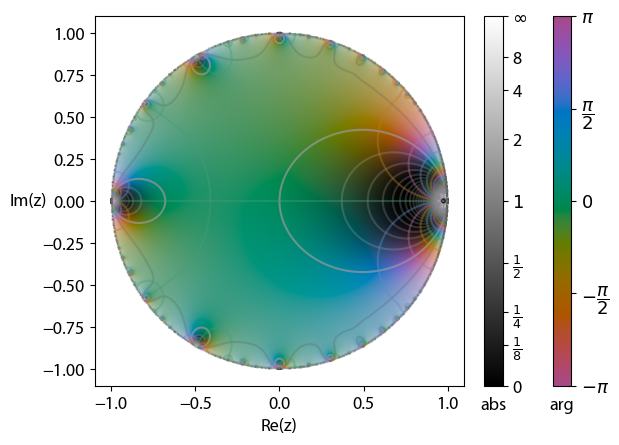
In mathematics, the Euler function is given by :\phi(q)=\prod_^\infty (1-q^k),\quad , q, <1. Named after Leonhard Euler, it is a model example of a q-series, ''q''-series and provides the prototypical example of a relation between combinatorics and complex analysis. Properties The coefficient in the formal power series expansion for gives the number of Partition of an integer, partitions of ''k''. That is, : where is the Partition function (number theory), partition function. The Euler identity, also known as the Pentagonal number theorem, is : is a pentagonal number. The Euler function is related to the Dedekind eta function as : The Euler function may be expressed as a q-Pochhammer symbol, ''q''-Pochhammer symbol: : T ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Function
In mathematics, the Euler function is given by :\phi(q)=\prod_^\infty (1-q^k),\quad , q, A000203 On account of the identity \sum_ d = \sum_ \frac, this may also be written as :\ln(\phi(q)) = -\sum_^\infty \frac \sum_ d. Also if a,b\in\mathbb^+ and ab=\pi ^2, then :a^e^\phi (e^)=b^e^\phi (e^). Special values The next identities come from Ramanujan's Notebooks: : \phi(e^)=\frac : \phi(e^)=\frac : \phi(e^)=\frac : \phi(e^)=\frac(\sqrt-1)^ Using the Pentagonal number theorem, exchanging sum and integral In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ..., and then invoking complex-analytic methods, one derives : \int_0^1\phi(q)\,\mathrmq = \frac. References Notes Other * {{Leonhard Euler Number theory Q-analogs Leonhard Euler km:អនុគមន៍អឺលែ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The ''n''th pentagonal number ''pn'' is the number of ''distinct'' dots in a pattern of dots consisting of the ''outlines'' of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside. ''p''n is given by the formula: :p_n = =\binom+3\binom for ''n'' ≥ 1. The first few pentagonal numbers are: 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an integral assigns numbers to functions in a way that describes Displacement (geometry), displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with Derivative, differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Srinivasa Ramanujan
Srinivasa Ramanujan (; born Srinivasa Ramanujan Aiyangar, ; 22 December 188726 April 1920) was an Indian mathematician. Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation: according to Hans Eysenck: "He tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered". Seeking mathematicians who could better understand his work, in 1913 he began a postal correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognising Ramanujan's work as extraordinary, Hardy arranged for him to travel to Cambridge. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OEIS
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is chairman of the OEIS Foundation. OEIS records information on integer sequences of interest to both professional and amateur mathematicians, and is widely cited. , it contains over 350,000 sequences, making it the largest database of its kind. Each entry contains the leading terms of the sequence, keywords, mathematical motivations, literature links, and more, including the option to generate a graph or play a musical representation of the sequence. The database is searchable by keyword, by subsequence, or by any of 16 fields. History Neil Sloane started collecting integer sequences as a graduate student in 1965 to support his work in combinatorics. The database was at first stored on punched cards. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Series
In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form :S(q)=\sum_^\infty a_n \frac . It can be resumed formally by expanding the denominator: :S(q)=\sum_^\infty a_n \sum_^\infty q^ = \sum_^\infty b_m q^m where the coefficients of the new series are given by the Dirichlet convolution of ''a''''n'' with the constant function 1(''n'') = 1: :b_m = (a*1)(m) = \sum_ a_n. \, This series may be inverted by means of the Möbius inversion formula, and is an example of a Möbius transform. Examples Since this last sum is a typical number-theoretic sum, almost any natural multiplicative function will be exactly summable when used in a Lambert series. Thus, for example, one has :\sum_^\infty q^n \sigma_0(n) = \sum_^\infty \frac where \sigma_0(n)=d(n) is the number of positive divisors of the number ''n''. For the higher order sum-of-divisor functions, one has :\sum_^\infty q^n \sigma_\alpha(n) = \sum_^\infty \frac where \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q-Pochhammer Symbol
In mathematical area of combinatorics, the ''q''-Pochhammer symbol, also called the ''q''-shifted factorial, is the product (a;q)_n = \prod_^ (1-aq^k)=(1-a)(1-aq)(1-aq^2)\cdots(1-aq^), with (a;q)_0 = 1. It is a ''q''-analog of the Pochhammer symbol (x)_n = x(x+1)\dots(x+n-1), in the sense that \lim_ \frac = (x)_n. The ''q''-Pochhammer symbol is a major building block in the construction of ''q''-analogs; for instance, in the theory of basic hypergeometric series, it plays the role that the ordinary Pochhammer symbol plays in the theory of generalized hypergeometric series. Unlike the ordinary Pochhammer symbol, the ''q''-Pochhammer symbol can be extended to an infinite product: (a;q)_\infty = \prod_^ (1-aq^k). This is an analytic function of ''q'' in the interior of the unit disk, and can also be considered as a formal power series in ''q''. The special case \phi(q) = (q;q)_\infty=\prod_^\infty (1-q^k) is known as Euler's function, and is important in combinatorics, number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dedekind Eta Function
In mathematics, the Dedekind eta function, named after Richard Dedekind, is a modular form of weight 1/2 and is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive. It also occurs in bosonic string theory. Definition For any complex number with , let ; then the eta function is defined by, :\eta(\tau) = e^\frac \prod_^\infty \left(1-e^\right) = q^\frac \prod_^\infty \left(1 - q^n\right) . Raising the eta equation to the 24th power and multiplying by gives :\Delta(\tau)=(2\pi)^\eta^(\tau) where is the modular discriminant. The presence of 24 can be understood by connection with other occurrences, such as in the 24-dimensional Leech lattice. The eta function is holomorphic on the upper half-plane but cannot be continued analytically beyond it. The eta function satisfies the functional equations :\begin \eta(\tau+1) &=e^\frac\eta(\tau),\\ \eta\left(-\frac\right) &= \sqrt\, \eta(\tau).\, \end In the second equation the bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Number Theorem
In mathematics, the pentagonal number theorem, originally due to Euler, relates the product and series representations of the Euler function. It states that :\prod_^\left(1-x^\right)=\sum_^\left(-1\right)^x^=1+\sum_^\infty(-1)^k\left(x^+x^\right). In other words, :(1-x)(1-x^2)(1-x^3) \cdots = 1 - x - x^2 + x^5 + x^7 - x^ - x^ + x^ + x^ - \cdots. The exponents 1, 2, 5, 7, 12, ... on the right hand side are given by the formula for ''k'' = 1, −1, 2, −2, 3, ... and are called (generalized) pentagonal numbers . (The constant term 1 corresponds to k=0.) This holds as an identity of convergent power series for , x, ''s'', take the rightmost 45-degree line and move it to form a new row, as in the matching diagram below. : If m ≤ s (as in our newly formed diagram where ''m'' = 2, ''s'' = 5) we may reverse the process by moving the bottom row to form a new 45 degree line (adding 1 element to each of the first ''m'' rows), taking us back to the first diagram. A bit of though ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Mathematics")