|
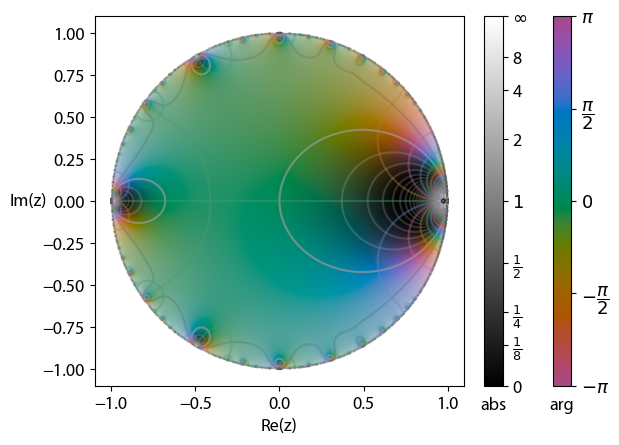
Euler's Function
In mathematics, the Euler function is given by :\phi(q)=\prod_^\infty (1-q^k),\quad , q, A000203 On account of the identity \sigma(n) = \sum_ d = \sum_ \frac , where \sigma(n) is the sum-of-divisors function, this may also be written as :\ln(\phi(q)) = -\sum_^\infty \frac\ q^n. Also if a,b\in\mathbb^+ and ab=\pi ^2, then :a^e^\phi (e^)=b^e^\phi (e^). Special values The next identities come from Ramanujan's Notebooks: : \phi(e^)=\frac : \phi(e^)=\frac : \phi(e^)=\frac : \phi(e^)=\frac(\sqrt-1)^ Using the Pentagonal number theorem, exchanging sum and integral In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ..., and then invoking complex-analytic methods, one derives : \int_0^1\phi(q)\,\mathrmq = \frac. References * {{Leonhard Euler Number theory Q-analogs Leonh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Function
In mathematics, the Euler function is given by :\phi(q)=\prod_^\infty (1-q^k),\quad , q, <1. Named after Leonhard Euler, it is a model example of a q-series, ''q''-series and provides the prototypical example of a relation between combinatorics and complex analysis. Properties The coefficient in the formal power series expansion for gives the number of Partition of an integer, partitions of ''k''. That is, : where is the Partition function (number theory), partition function. The Euler identity, also known as the Pentagonal number theorem, is : is a pentagonal number. The Euler function is related to the Dedekind eta function as : The Euler function may be expressed as a q-Pochhammer symbol, ''q''-Pochhammer symbol: : ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dedekind Eta Function
In mathematics, the Dedekind eta function, named after Richard Dedekind, is a modular form of weight 1/2 and is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive. It also occurs in bosonic string theory. Definition For any complex number with , let ; then the eta function is defined by, :\eta(\tau) = e^\frac \prod_^\infty \left(1-e^\right) = q^\frac \prod_^\infty \left(1 - q^n\right) . Raising the eta equation to the 24th power and multiplying by gives :\Delta(\tau)=(2\pi)^\eta^(\tau) where is the modular discriminant. The presence of 24 can be understood by connection with other occurrences, such as in the 24-dimensional Leech lattice. The eta function is holomorphic on the upper half-plane but cannot be continued analytically beyond it. The eta function satisfies the functional equations :\begin \eta(\tau+1) &=e^\frac\eta(\tau),\\ \eta\left(-\frac\right) &= \sqrt\, \eta(\tau).\, \end In the second equation the b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Srinivasa Ramanujan
Srinivasa Ramanujan Aiyangar (22 December 188726 April 1920) was an Indian mathematician. Often regarded as one of the greatest mathematicians of all time, though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation. According to Hans Eysenck, "he tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered". Seeking mathematicians who could better understand his work, in 1913 he began a mail correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognising Ramanujan's work as extraordinary, Hardy arranged ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function ''σ''''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OEIS
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009, and is its chairman. OEIS records information on integer sequences of interest to both professional and amateur mathematicians, and is widely cited. , it contains over 370,000 sequences, and is growing by approximately 30 entries per day. Each entry contains the leading terms of the sequence, keywords, mathematical motivations, literature links, and more, including the option to generate a graph or play a musical representation of the sequence. The database is searchable by keyword, by subsequence, or by any of 16 fields. There is also an advanced search function called SuperSeeker which runs a large number of different algorithms to identify sequences related to the input. History Neil Sloane started coll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Series
In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form :S(q)=\sum_^\infty a_n \frac . It can be resummed formally by expanding the denominator: :S(q)=\sum_^\infty a_n \sum_^\infty q^ = \sum_^\infty b_m q^m where the coefficients of the new series are given by the Dirichlet convolution of ''a''''n'' with the constant function 1(''n'') = 1: :b_m = (a*1)(m) = \sum_ a_n. \, This series may be inverted by means of the Möbius inversion formula, and is an example of a Möbius transform. Examples Since this last sum is a typical number-theoretic sum, almost any natural multiplicative function will be exactly summable when used in a Lambert series. Thus, for example, one has :\sum_^\infty q^n \sigma_0(n) = \sum_^\infty \frac where \sigma_0(n)=d(n) is the number of positive divisors of the number ''n''. For the higher order sum-of-divisor functions, one has :\sum_^\infty q^n \sigma_\alpha(n) = \sum_^\infty \frac = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q-Pochhammer Symbol
In the mathematical field of combinatorics, the ''q''-Pochhammer symbol, also called the ''q''-shifted factorial, is the product (a;q)_n = \prod_^ (1-aq^k)=(1-a)(1-aq)(1-aq^2)\cdots(1-aq^), with (a;q)_0 = 1. It is a ''q''-analog of the Pochhammer symbol (x)_n = x(x+1)\dots(x+n-1), in the sense that \lim_ \frac = (x)_n. The ''q''-Pochhammer symbol is a major building block in the construction of ''q''-analogs; for instance, in the theory of basic hypergeometric series, it plays the role that the ordinary Pochhammer symbol plays in the theory of generalized hypergeometric series. Unlike the ordinary Pochhammer symbol, the ''q''-Pochhammer symbol can be extended to an infinite product: (a;q)_\infty = \prod_^ (1-aq^k). This is an analytic function of ''q'' in the interior of the unit disk, and can also be considered as a formal power series in ''q''. The special case \phi(q) = (q;q)_\infty=\prod_^\infty (1-q^k) is known as Euler's function, and is important in combinatorics, number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Number
A pentagonal number is a figurate number that extends the concept of triangular number, triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotational symmetry, rotationally symmetrical. The ''n''th pentagonal number ''pn'' is the number of ''distinct'' dots in a pattern of dots consisting of the ''outlines'' of regular pentagons with sides up to n dots, when the pentagons are overlaid so that they share one vertex (geometry), vertex. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside. ''p''n is given by the formula: :p_n = =\binom+3\binom for ''n'' ≥ 1. The first few pentagonal numbers are: 1 (number), 1, 5 (number), 5, 12 (number), 12, 22 (number), 22, 35 (number), 35, 51 (number), 51, 70 (number), 70, 92 (number), 92, 117 (nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |