|
Ergun Equation
The Ergun equation, derived by the Turkish chemical engineer Sabri Ergun in 1952, expresses the friction factor in a packed column as a function of the modified Reynolds number. Equation f_p = \frac +1.75 where f_p and Gr_p are defined as f_p = \frac \frac \left(\frac\right) and Gr_p = \frac = \frac; where: Gr_p is the modified Reynolds number, f_p is the packed bed friction factor \Delta p is the pressure drop across the bed, L is the length of the bed (not the column), D_p is the equivalent spherical diameter of the packing, \rho is the density of fluid, \mu is the dynamic viscosity of the fluid, v_s is the superficial velocity (i.e. the velocity that the fluid would have through the empty tube at the same volumetric flow rate) \epsilon is the void fraction (porosity) of the bed. Re is the particle Reynolds Number (based on superficial velocity [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turkey
Turkey ( tr, Türkiye ), officially the Republic of Türkiye ( tr, Türkiye Cumhuriyeti, links=no ), is a list of transcontinental countries, transcontinental country located mainly on the Anatolia, Anatolian Peninsula in Western Asia, with a East Thrace, small portion on the Balkans, Balkan Peninsula in Southeast Europe. It shares borders with the Black Sea to the north; Georgia (country), Georgia to the northeast; Armenia, Azerbaijan, and Iran to the east; Iraq to the southeast; Syria and the Mediterranean Sea to the south; the Aegean Sea to the west; and Greece and Bulgaria to the northwest. Cyprus is located off the south coast. Turkish people, Turks form the vast majority of the nation's population and Kurds are the largest minority. Ankara is Turkey's capital, while Istanbul is its list of largest cities and towns in Turkey, largest city and financial centre. One of the world's earliest permanently Settler, settled regions, present-day Turkey was home to important Neol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
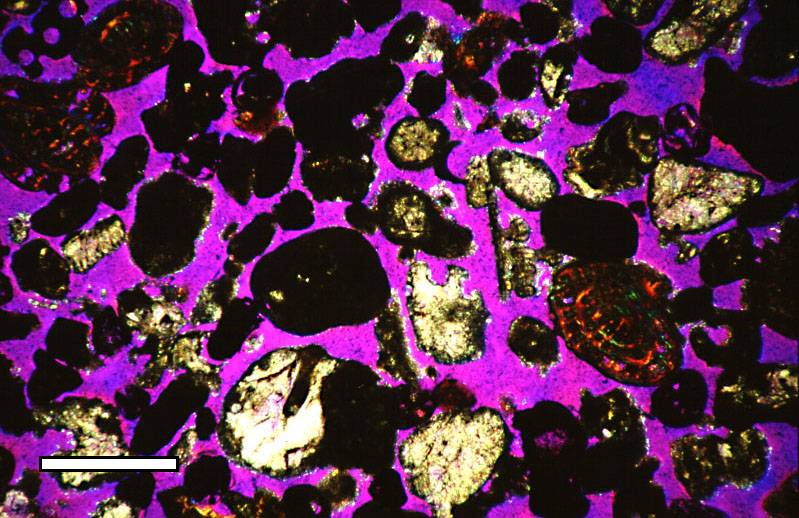
Porosity
Porosity or void fraction is a measure of the void (i.e. "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure the "accessible void", the total amount of void space accessible from the surface (cf. closed-cell foam). There are many ways to test porosity in a substance or part, such as industrial CT scanning. The term porosity is used in multiple fields including pharmaceutics, ceramics, metallurgy, materials, manufacturing, petrophysics, hydrology, earth sciences, soil mechanics, and engineering. Void fraction in two-phase flow In gas-liquid two-phase flow, the void fraction is defined as the fraction of the flow-channel volume that is occupied by the gas phase or, alternatively, as the fraction of the cross-sectional area of the channel that is occupied by the gas phase. Void fraction usually varies from location to location in the fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in French an ''équation'' is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation. ''Solving'' an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables. An equation is written as two expressions, connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kozeny–Carman Equation
The Kozeny–Carman equation (or Carman–Kozeny equation or Kozeny equation) is a relation used in the field of fluid dynamics to calculate the pressure drop of a fluid flowing through a packed bed of solids. It is named after Josef Kozeny and Philip C. Carman. The equation is only valid for creeping flow, i.e. in the slowest limit of laminar flow. The equation was derived by Kozeny (1927) and Carman (1937, 1956) from a starting point of (a) modelling fluid flow in a packed bed as laminar fluid flow in a collection of curving passages/tubes crossing the packed bed and (b) Poiseuille's law describing laminar fluid flow in straight, circular section pipes. Equation The equation is given as: :\frac = - \frac\fracu_\mathrm where: *\Delta p is the pressure drop; *L is the total height of the bed; *u_\mathrm is the superficial or "empty-tower" velocity; *\mu is the viscosity of the fluid; *\epsilon is the porosity of the bed; *\mathit_\mathrm is the sphericity of the particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hagen–Poiseuille Equation
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845. The assumptions of the equation are that the fluid is incompressible and Newtonian; the flow is laminar through a pipe of constant circular cross-section that is substantially longer than its diameter; and there is no acceleration of fluid in the pipe. For velocities and pipe diam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluidized Bed
A fluidized bed is a physical phenomenon that occurs when a solid particulate substance (usually present in a holding vessel) is under the right conditions so that it behaves like a fluid. The usual way to achieve a fluidize bed is to pump pressurized fluid into the particles. The resulting medium then has many properties and characteristics of normal fluids, such as the ability to free-flow under gravity, or to be pumped using fluid technologies. The resulting phenomenon is called fluidization. Fluidized beds are used for several purposes, such as fluidized bed reactors (types of chemical reactors), solids separation, fluid catalytic cracking, fluidized bed combustion, heat or mass transfer or interface modification, such as applying a coating onto solid items. This technique is also becoming more common in aquaculture for the production of shellfish in integrated multi-trophic aquaculture systems. Properties A fluidized bed consists of fluid-solid mixture that exhibits flui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darcy's Law
Darcy's law is an equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on results of experiments on the flow of water through beds of sand, forming the basis of hydrogeology, a branch of earth sciences. It is analogous to Ohm's law in electrostatics, linearly relating the volume flow rate of the fluid to the hydraulic head difference (which is often just proportional to the pressure difference) via the hydraulic conductivity. Background Darcy's law was first determined experimentally by Darcy, but has since been derived from the Navier–Stokes equations via homogenization methods. It is analogous to Fourier's law in the field of heat conduction, Ohm's law in the field of electrical networks, and Fick's law in diffusion theory. One application of Darcy's law is in the analysis of water flow through an aquifer; Darcy's law along with the equation of conservation of mass simplifies to the groundwater flow equation, on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laminar Flow
In fluid dynamics, laminar flow is characterized by fluid particles following smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection. When a fluid is flowing through a closed channel such as a pipe or between two flat plates, either of two types of flow may occur depending on the velocity and viscosity of the fluid: laminar flow or turbulent flow. Laminar flow occurs at lower velocities, below a threshold at which the flow becomes turbulent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superficial Velocity
Superficial velocity (or superficial flow velocity), in engineering of multiphase flows and flows in porous media, is a hypothetical (artificial) flow velocity calculated as if the given phase or fluid were the only one flowing or present in a given cross sectional area. Other phases, particles, the skeleton of the porous medium, etc. present in the channel are disregarded. Superficial velocity is used in many engineering equations because it is the value which is usually readily known and unambiguous, whereas real velocity is often variable from place to place. Superficial velocity can be expressed as: :u_s = \frac {A} where: * us - superficial velocity of a given phase, m/s * Q - volume flow rate of the phase, m3/s * A - cross sectional area, m2 Using the concept of porosity, the dependence between the advection velocity and the superficial velocity can be expressed as (for one-dimensional flow): : u_s = \phi u where: *\phi is porosity, dimensionless *u is the average fluid ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Engineer
In the field of engineering, a chemical engineer is a professional, equipped with the knowledge of chemical engineering, who works principally in the chemical industry to convert basic raw materials into a variety of products and deals with the design and operation of plants and equipment. In general, a chemical engineer is one who applies and uses principles of chemical engineering in any of its various practical applications; these often include # design, manufacture, and operation of plants and machinery in industrial chemical and related processes ("chemical process engineers"); # development of new or adapted substances for products ranging from foods and beverages to cosmetics to cleaners to pharmaceutical ingredients, among many other products ("chemical product engineers"); and # development of new technologies such as fuel cells, hydrogen power and nanotechnology, as well as working in fields wholly or partially derived from chemical engineering such as materials scie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |