|
Erdős–Gallai Theorem
The Erdős–Gallai theorem is a result in graph theory, a branch of combinatorial mathematics. It provides one of two known approaches to solving the graph realization problem, i.e. it gives a necessary and sufficient condition for a finite sequence of natural numbers to be the degree sequence of a simple graph. A sequence obeying these conditions is called "graphic". The theorem was published in 1960 by Paul Erdős and Tibor Gallai, after whom it is named. Statement A sequence of non-negative integers d_1\geq\cdots\geq d_n can be represented as the degree sequence of a finite simple graph on ''n'' vertices if and only if d_1+\cdots+d_n is even and : \sum^_d_i\leq k(k-1)+ \sum^n_ \min (d_i,k) holds for every k in 1\leq k\leq n. Proofs It is not difficult to show that the conditions of the Erdős–Gallai theorem are necessary for a sequence of numbers to be graphic. The requirement that the sum of the degrees be even is the handshaking lemma, already used by Euler in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by ''edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flow Network
In graph theory, a flow network (also known as a transportation network) is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A network can be used to model traffic in a computer network, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes. Definition A network is a graph , where is a set of vertices and is a set of 's edges – a subset of – together with a non-negative function , called the capacity function. Without loss of generality, we may assume t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics (journal)
''Discrete Mathematics'' is a biweekly peer-reviewed scientific journal in the broad area of discrete mathematics, combinatorics, graph theory, and their applications. It was established in 1971 and is published by North-Holland Publishing Company. It publishes both short notes, full length contributions, as well as survey articles. In addition, the journal publishes a number of special issues each year dedicated to a particular topic. Although originally it published articles in French and German, it now allows only English language articles. The editor-in-chief is Douglas West ( University of Illinois, Urbana). History The journal was established in 1971. The very first article it published was written by Paul Erdős, who went on to publish a total of 84 papers in the journal. Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor of 0.87. Notable publications * The 1972 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Havel–Hakimi Algorithm
The Havel–Hakimi algorithm is an algorithm in graph theory solving the graph realization problem. That is, it answers the following question: ''Given a finite list of nonnegative integers in non-increasing order, is there a simple graph such that its degree sequence is exactly this list?'' A simple graph contains no double edges or loops. The degree sequence is a list of numbers in nonincreasing order indicating the number of edges incident to each vertex in the graph.From Shahriari (2022, p. 355): "Definition 10.6 (The degree sequence of a graph; Graphic sequences). The ''degree sequence'' of a graph is the list of the degrees of its vertices in non-increasing order. A non-increasing sequence of non-negative integers is called ''graphic'', if there exists a simple graph whose degree sequence is precisely that sequence.” If a simple graph exists for exactly the given degree sequence, the list of integers is called ''graphic''. The Havel-Hakimi algorithm constructs a special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
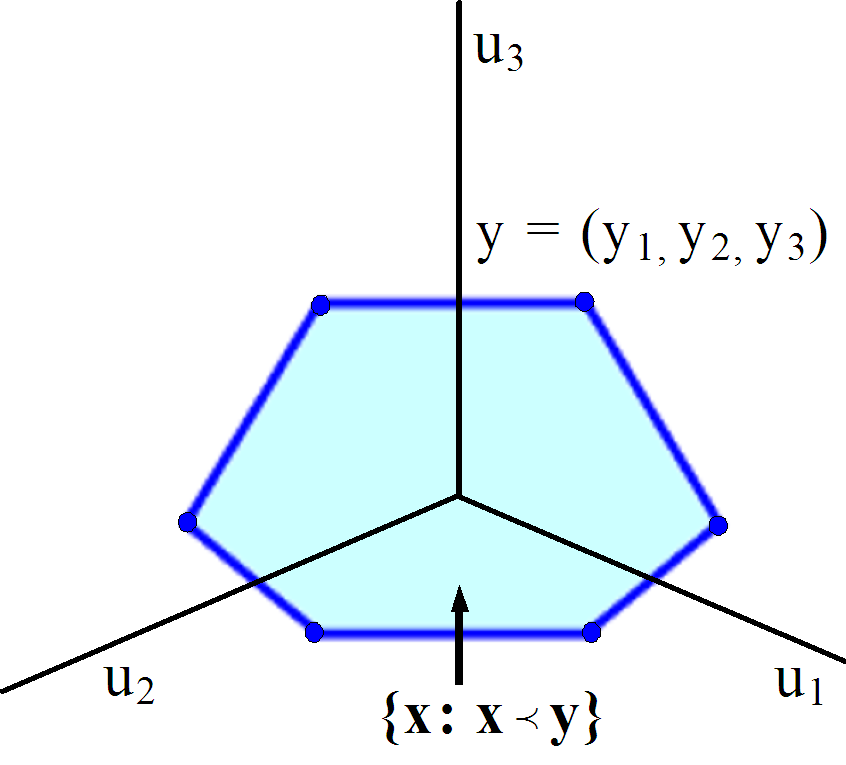
Majorization
In mathematics, majorization is a preorder on vectors of real numbers. Let ^_,\ i=1,\,\ldots,\,n denote the i-th largest element of the vector \mathbf\in\mathbb^n. Given \mathbf,\ \mathbf \in \mathbb^n, we say that \mathbf weakly majorizes (or dominates) \mathbf from below (or equivalently, we say that \mathbf is weakly majorized (or dominated) by \mathbf from below) denoted as \mathbf \succ_w \mathbf if \sum_^k x_^ \geq \sum_^k y_^ for all k=1,\,\dots,\,d. If in addition \sum_^d x_i^ = \sum_^d y_i^, we say that \mathbf majorizes (or dominates) \mathbf , written as \mathbf \succ \mathbf , or equivalently, we say that \mathbf is majorized (or dominated) by \mathbf. The order of the entries of the vectors \mathbf or \mathbf does not affect the majorization, e.g., the statement (1,2)\prec (0,3) is simply equivalent to (2,1)\prec (3,0). As a consequence, majorization is not a partial order, since \mathbf \succ \mathbf and \mathbf \succ \mathbf do not imply \mathbf = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gale–Ryser Theorem
The Gale–Ryser theorem is a result in graph theory and combinatorial matrix theory, two branches of combinatorics. It provides one of two known approaches to solving the bipartite realization problem, i.e. it gives a necessary and sufficient condition for two finite sequences of natural numbers to be the degree sequence of a labeled simple bipartite graph; a sequence obeying these conditions is called "bigraphic". It is an analog of the Erdős–Gallai theorem for simple graphs. The theorem was published independently in 1957 by H. J. Ryser and David Gale. Statement A pair of sequences of nonnegative integers (a_1,\ldots,a_n) and (b_1,\ldots,b_n) with a_1\geq\cdots\geq a_n is bigraphic if and only if \sum_^a_i=\sum_^b_i and the following inequality holds for all k \in \: : \sum^k_ a_i\leq \sum^n_ \min(b_i,k). Sometimes this theorem is stated with the additional constraint b_1\geq\cdots\geq b_n. This condition is not necessary, because the labels of vertices of one partite set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fulkerson–Chen–Anstee Theorem
The Fulkerson–Chen–Anstee theorem is a result in graph theory, a branch of combinatorics. It provides one of two known approaches solving the digraph realization problem, i.e. it gives a necessary and sufficient condition for pairs of nonnegative integers ((a_1,b_1),\ldots,(a_n,b_n)) to be the indegree-outdegree pairs of a simple directed graph; a sequence obeying these conditions is called "digraphic". D. R. FulkersonD.R. Fulkerson: ''Zero-one matrices with zero trace.'' In: ''Pacific J. Math.'' No. 12, 1960, pp. 831–836 (1960) obtained a characterization analogous to the classical Erdős–Gallai theorem for graphs, but in contrast to this solution with exponentially many inequalities. In 1966 Chen Wai-Kai Chen: ''On the realization of a (''p'',''s'')-digraph with prescribed degrees .'' In: ''Journal of the Franklin Institute'' No. 6, 1966, pp. 406–422 improved this result in demanding the additional constraint that the integer pairs must be sorted in non-increasing lexicog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferrers Diagram
In number theory and combinatorics, a partition of a positive integer , also called an integer partition, is a way of writing as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition.) For example, can be partitioned in five distinct ways: : : : : : The order-dependent composition is the same partition as , and the two distinct compositions and represent the same partition as . A summand in a partition is also called a part. The number of partitions of is given by the partition function . So . The notation means that is a partition of . Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation theory in general. Examples The seven partitions of 5 are: * 5 * 4 + 1 * 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (order)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join (mathematics), join) and a unique infimum (also called a greatest lower bound or meet (mathematics), meet). An example is given by the power set of a set, partially ordered by Subset, inclusion, for which the supremum is the Union (set theory), union and the infimum is the Intersection (set theory), intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic Identity (mathematics), identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilatti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Sum
In computer science, the prefix sum, cumulative sum, inclusive scan, or simply scan of a sequence of numbers is a second sequence of numbers , the sums of prefixes (running totals) of the input sequence: : : : :... For instance, the prefix sums of the natural numbers are the triangular numbers: : Prefix sums are trivial to compute in sequential models of computation, by using the formula to compute each output value in sequence order. However, despite their ease of computation, prefix sums are a useful primitive in certain algorithms such as counting sort,. and they form the basis of the scan higher-order function in functional programming languages. Prefix sums have also been much studied in parallel algorithms, both as a test problem to be solved and as a useful primitive to be used as a subroutine in other parallel algorithms.. Abstractly, a prefix sum requires only a binary associative operator ⊕, making it useful for many applications from calculating well-separated pair ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majorization
In mathematics, majorization is a preorder on vectors of real numbers. Let ^_,\ i=1,\,\ldots,\,n denote the i-th largest element of the vector \mathbf\in\mathbb^n. Given \mathbf,\ \mathbf \in \mathbb^n, we say that \mathbf weakly majorizes (or dominates) \mathbf from below (or equivalently, we say that \mathbf is weakly majorized (or dominated) by \mathbf from below) denoted as \mathbf \succ_w \mathbf if \sum_^k x_^ \geq \sum_^k y_^ for all k=1,\,\dots,\,d. If in addition \sum_^d x_i^ = \sum_^d y_i^, we say that \mathbf majorizes (or dominates) \mathbf , written as \mathbf \succ \mathbf , or equivalently, we say that \mathbf is majorized (or dominated) by \mathbf. The order of the entries of the vectors \mathbf or \mathbf does not affect the majorization, e.g., the statement (1,2)\prec (0,3) is simply equivalent to (2,1)\prec (3,0). As a consequence, majorization is not a partial order, since \mathbf \succ \mathbf and \mathbf \succ \mathbf do not imply \mathbf = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition (number Theory)
In number theory and combinatorics, a partition of a positive integer , also called an integer partition, is a way of writing as a summation, sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition (combinatorics), composition.) For example, can be partitioned in five distinct ways: : : : : : The order-dependent composition is the same partition as , and the two distinct compositions and represent the same partition as . A summand in a partition is also called a part. The number of partitions of is given by the partition function . So . The notation means that is a partition of . Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation, group representation theory in genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |