|
Equivalence Class Partitioning
Equivalence partitioning or equivalence class partitioning (ECP) is a software testing technique that divides the input data of a software unit into partitions of equivalent data from which test cases can be derived. In principle, test cases are designed to cover each partition at least once. This technique tries to define test cases that uncover classes of errors, thereby reducing the total number of test cases that must be developed. An advantage of this approach is reduction in the time required for testing software due to lesser number of test cases. Equivalence partitioning is typically applied to the inputs of a tested component, but may be applied to the outputs in rare cases. The equivalence partitions are usually derived from the requirements specification for input attributes that influence the processing of the test object. The fundamental concept of ECP comes from equivalence class which in turn comes from equivalence relation. A software system is in effect a computa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Software Testing
Software testing is the act of examining the artifacts and the behavior of the software under test by validation and verification. Software testing can also provide an objective, independent view of the software to allow the business to appreciate and understand the risks of software implementation. Test techniques include, but not necessarily limited to: * analyzing the product requirements for completeness and correctness in various contexts like industry perspective, business perspective, feasibility and viability of implementation, usability, performance, security, infrastructure considerations, etc. * reviewing the product architecture and the overall design of the product * working with product developers on improvement in coding techniques, design patterns, tests that can be written as part of code based on various techniques like boundary conditions, etc. * executing a program or application with the intent of examining behavior * reviewing the deployment infrastructure a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \,\sim\, on S, the of an element a in S, denoted by is the set \ of elements which are equivalent to a. It may be proven, from the defining properties of equivalence relations, that the equivalence classes form a partition of S. This partition—the set of equivalence classes—is sometimes called the quotient set or the quotient space of S by \,\sim\,, and is denoted by S / \sim. When the set S has some structure (such as a group operation or a topology) and the equivalence relation \,\sim\, is compatible with this structure, the quotient set often inherits a similar structure from its parent set. Ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes. Two elements of the given set are equivalent to each other if and only if they belong to the same equivalence class. Notation Various notations are used in the literature to denote that two elements a and b of a set are equivalent with respect to an equivalence relation R; the most common are "a \sim b" and "", which are used when R is implicit, and variations of "a \sim_R b", "", or "" to specify R explicitly. Non-equivalence may be written "" or "a \not\equiv b". Definition A binary relation \,\sim\, on a set X is said to be an equivalence relation, if and only if it is reflexive, symmetric and transitive. That is, for all a, b, and c in X: * a \sim a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computable Function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithms, in the sense that a function is computable if there exists an algorithm that can do the job of the function, i.e. given an input of the function domain it can return the corresponding output. Computable functions are used to discuss computability without referring to any concrete model of computation such as Turing machines or register machines. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions. Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the general recursive functions. Before the precise definition of computable function, mathematicians often used the informal term ''effectively calculable''. This term has since come to be identified with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm can be expressed within a finite amount of spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programming Language
A programming language is a system of notation for writing computer programs. Most programming languages are text-based formal languages, but they may also be graphical. They are a kind of computer language. The description of a programming language is usually split into the two components of syntax (form) and semantics (meaning), which are usually defined by a formal language. Some languages are defined by a specification document (for example, the C programming language is specified by an ISO Standard) while other languages (such as Perl) have a dominant implementation that is treated as a reference. Some languages have both, with the basic language defined by a standard and extensions taken from the dominant implementation being common. Programming language theory is the subfield of computer science that studies the design, implementation, analysis, characterization, and classification of programming languages. Definitions There are many considerations when defining ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Test Vector
In computer science and engineering, a test vector is a set of inputs provided to a system in order to test that system. In software development, test vectors are a methodology of software testing and software verification and validation. Rationale In computer science and engineering, a system acts as a computable function. An example of a specific function could be y = f(x) where y is the output of the system and x is the input; however, most systems' inputs are not one-dimensional. When the inputs are multi-dimensional, we could say that the system takes the form y = f(x_1, x_2, ...) ; however, we can generalize this equation to a general form Y = C(X) where Y is the result of the system's execution, C belongs to the set of computable functions, and X is an input vector. While testing the system, various test vectors must be used to examine the system's behavior with differing inputs. Example For example, consider a login page with two input fields: a username field and a pas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Code Coverage
In computer science, test coverage is a percentage measure of the degree to which the source code of a program is executed when a particular test suite is run. A program with high test coverage has more of its source code executed during testing, which suggests it has a lower chance of containing undetected software bugs compared to a program with low test coverage. Many different metrics can be used to calculate test coverage. Some of the most basic are the percentage of program subroutines and the percentage of program statements called during execution of the test suite. Test coverage was among the first methods invented for systematic software testing. The first published reference was by Miller and Maloney in '' Communications of the ACM'', in 1963. Coverage criteria To measure what percentage of code has been executed by a test suite, one or more ''coverage criteria'' are used. These are usually defined as rules or requirements, which a test suite must satisfy. Basi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
C (programming Language)
C (''pronounced like the letter c'') is a General-purpose language, general-purpose computer programming language. It was created in the 1970s by Dennis Ritchie, and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted CPUs. It has found lasting use in operating systems, device drivers, protocol stacks, though decreasingly for application software. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the measuring programming language popularity, most widely used programming languages, with C compilers avail ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequation
In mathematics, an inequation is a statement that an inequality holds between two values. It is usually written in the form of a pair of expressions denoting the values in question, with a relational sign between them indicating the specific inequality relation. Some examples of inequations are: * a 1 * x \neq 0 In some cases, the term "inequation" can be considered synonymous to the term "inequality", while in other cases, an inequation is reserved only for statements whose inequality relation is "not equal to" (≠). Chains of inequations A shorthand notation is used for the conjunction of several inequations involving common expressions, by chaining them together. For example, the chain :0 \leq a < b \leq 1 is shorthand for : which also implies that and . In rare cases, chains without such implications about distant terms are used. For example |
Integer (computer Science)
In computer science, an integer is a datum of integral data type, a data type that represents some range of mathematical integers. Integral data types may be of different sizes and may or may not be allowed to contain negative values. Integers are commonly represented in a computer as a group of binary digits (bits). The size of the grouping varies so the set of integer sizes available varies between different types of computers. Computer hardware nearly always provides a way to represent a processor register or memory address as an integer. Value and representation The ''value'' of an item with an integral type is the mathematical integer that it corresponds to. Integral types may be ''unsigned'' (capable of representing only non-negative integers) or ''signed'' (capable of representing negative integers as well). An integer value is typically specified in the source code of a program as a sequence of digits optionally prefixed with + or −. Some programming languages allow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
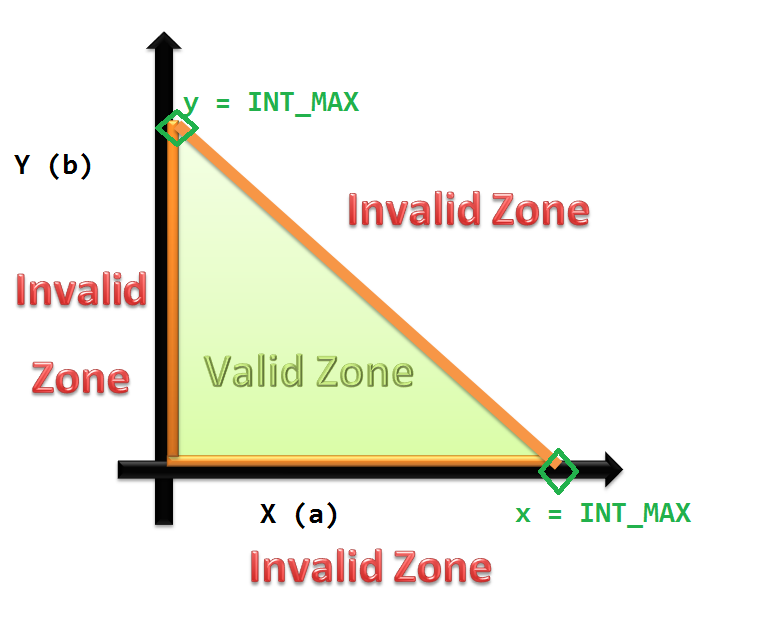
Boundary-value Analysis
Boundary-value analysis is a software testing technique in which tests are designed to include representatives of boundary values in a range. The idea comes from the boundary. Given that we have a set of test vectors to test the system, a topology can be defined on that set. Those inputs which belong to the same equivalence class as defined by the equivalence partitioning theory would constitute the basis. Given that the basis sets are neighbors, there would exist a boundary between them. The test vectors on either side of the boundary are called boundary values. In practice this would require that the test vectors can be ordered, and that the individual parameters follows some kind of order (either partial order or total order). Formal definition Formally the boundary values can be defined as below: :Let the set of the test vectors be . :Let's assume that there is an ordering relation defined over them, as . :Let be two equivalent classes. :Assume that test vector and . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |