|
End-to-end Vector
In the physical chemistry study of polymers, the end-to-end vector is the vector that points from one end of a polymer to the other end. If each monomer unit in a polymer is represented by a point in space, the translation vectors \vec_i connect between these points. The end-to-end vector \vec is the sum of these translation vectors: :\vec = \sum_i \vec_i The norm of the end-to-end vector is called the end-to-end distance. Relation to other quantities The quadratic mean of the end-to-end distance \left\langle r^2 \right\rangle can be related to the quadratic mean of the radius of gyration \left\langle s^2 \right\rangle of a polymer by the relation:{{cite book, last1= Gedde , first1= Ulf W. , title= Polymer Physics , url= https://books.google.com/books?id=Iem3fC7XdnkC , year= 1995 , publisher= Springer , isbn= 0-412-62640-3 , page= 21 :\left\langle r^2 \right\rangle = 6 \left\langle s^2 \right\rangle Notes See also * Freely Jointed Chain * Worm-like chain The worm-like c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Chain Random Walk
Ideal may refer to: Philosophy * Ideal (ethics), values that one actively pursues as goals * Platonic ideal, a philosophical idea of trueness of form, associated with Plato Mathematics * Ideal (ring theory), special subsets of a ring considered in abstract algebra * Ideal, special subsets of a semigroup * Ideal (order theory), special kind of lower sets of an order * Ideal (set theory), a collection of sets regarded as "small" or "negligible" * Ideal (Lie algebra), a particular subset in a Lie algebra * Ideal point, a boundary point in hyperbolic geometry * Ideal triangle, a triangle in hyperbolic geometry whose vertices are ideal points Science * Ideal chain, in science, the simplest model describing a polymer * Ideal gas law, in physics, governing the pressure of an ideal gas * Ideal transformer, an electrical transformer having zero resistance and perfect magnetic threading * Ideal final result, in TRIZ methodology, the best possible solution * Thought experiment, sometimes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
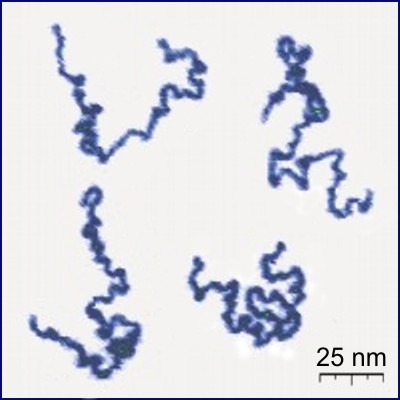
Polymer
A polymer (; Greek ''poly-'', "many" + '' -mer'', "part") is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compounds, produces unique physical properties including toughness, high elasticity, viscoelasticity, and a tendency to form amorphous and semicrystalline structures rather than crystals. The term "polymer" derives from the Greek word πολύς (''polus'', meaning "many, much") and μέρος (''meros'', mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a ''directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Mean
In mathematics and its applications, the root mean square of a set of numbers x_i (abbreviated as RMS, or rms and denoted in formulas as either x_\mathrm or \mathrm_x) is defined as the square root of the mean square (the arithmetic mean of the squares) of the set. The RMS is also known as the quadratic mean (denoted M_2) and is a particular case of the generalized mean. The RMS of a continuously varying function (denoted f_\mathrm) can be defined in terms of an integral of the squares of the instantaneous values during a cycle. For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. In estimation theory, the root-mean-square deviation of an estimator is a measure of the imperfection of the fit of the estimator to the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Gyration
''Radius of gyration'' or gyradius of a body about the axis of rotation is defined as the radial distance to a point which would have a moment of inertia the same as the body's actual distribution of mass, if the total mass of the body were concentrated there. Mathematically the radius of gyration is the root mean square distance of the object's parts from either its center of mass or a given axis, depending on the relevant application. It is actually the perpendicular distance from point mass to the axis of rotation. One can represent a trajectory of a moving point as a body. Then radius of gyration can be used to characterize the typical distance travelled by this point. Suppose a body consists of n particles each of mass m. Let r_1, r_2, r_3, \dots , r_n be their perpendicular distances from the axis of rotation. Then, the moment of inertia I of the body about the axis of rotation is :I = m_1 r_1^2 + m_2 r_2^2 + \cdots + m_n r_n^2 : If all the masses are the same (m), the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Worm-like Chain
The worm-like chain (WLC) model in polymer physics is used to describe the behavior of polymers that are semi-flexible: fairly stiff with successive segments pointing in roughly the same direction, and with persistence length within a few orders of magnitude of the polymer length. The WLC model is the continuous version of the Kratky– Porod model. Model elements The WLC model envisions a continuously flexible isotropic rod. This is in contrast to the freely-jointed chain model, which is only flexible between discrete freely hinged segments. The model is particularly suited for describing stiffer polymers, with successive segments displaying a sort of cooperativity: nearby segments are roughly aligned. At room temperature, the polymer adopts a smoothly curved conformation; at T = 0 K, the polymer adopts a rigid rod conformation. For a polymer of maximum length L_0, parametrize the path of the polymer as s \in(0,L_0). Allow \hat t(s) to be the unit tangent vector to the chai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polymers
A polymer (; Greek ''poly-'', "many" + '' -mer'', "part") is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compounds, produces unique physical properties including toughness, high elasticity, viscoelasticity, and a tendency to form amorphous and semicrystalline structures rather than crystals. The term "polymer" derives from the Greek word πολύς (''polus'', meaning "many, much") and μέρος (''meros'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |