|
Effective Dimension
In mathematics, effective dimension is a modification of Hausdorff dimension and other fractal dimensions that places it in a computability theory setting. There are several variations (various notions of effective dimension) of which the most common is effective Hausdorff dimension. Dimension, in mathematics, is a particular way of describing the size of an object (contrasting with measure and other, different, notions of size). Hausdorff dimension generalizes the well-known integer dimensions assigned to points, lines, planes, etc. by allowing one to distinguish between objects of intermediate size between these integer-dimensional objects. For example, fractal subsets of the plane may have intermediate dimension between 1 and 2, as they are "larger" than lines or curves, and yet "smaller" than filled circles or rectangles. Effective dimension modifies Hausdorff dimension by requiring that objects with small effective dimension be not only small but also locatable (or partially lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Dimension
In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that was first introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
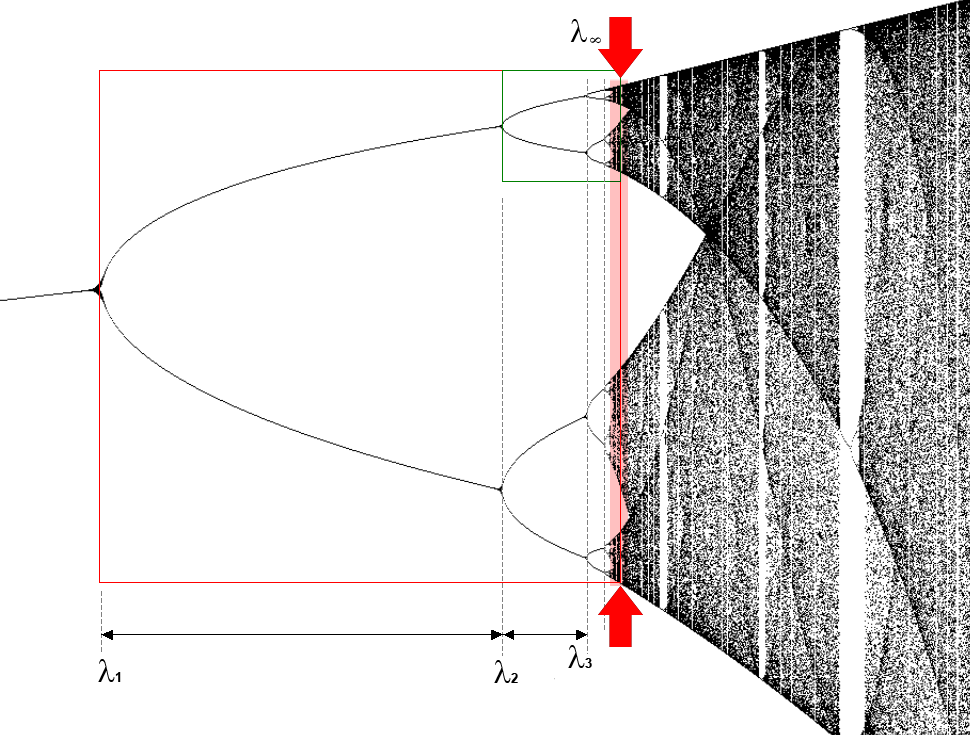
Fractal Dimension
In mathematics, more specifically in fractal geometry, a fractal dimension is a ratio providing a statistical index of complexity comparing how detail in a pattern (strictly speaking, a fractal pattern) changes with the scale at which it is measured. It has also been characterized as a measure of the space-filling capacity of a pattern that tells how a fractal scales differently from the space it is embedded in; a fractal dimension does not have to be an integer. The essential idea of "fractured" dimensions has a long history in mathematics, but the term itself was brought to the fore by Benoit Mandelbrot based on his 1967 paper on self-similarity in which he discussed ''fractional dimensions''. In that paper, Mandelbrot cited previous work by Lewis Fry Richardson describing the counter-intuitive notion that a coastline's measured length changes with the length of the measuring stick used ( see Fig. 1). In terms of that notion, the fractal dimension of a coastline quantifies ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computability Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of subrecursive hierarchies, formal methods, and formal languages. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A Surface (mathematics), surface, such as the Boundary (mathematics), boundary of a Cylinder (geometry), cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the Euclidean plane, plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Fractals By Hausdorff Dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff dimension, Hausdorff-Besicovitch dimension strictly exceeds the topological dimension." Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to illustrate what it means for a fractal to have a low or a high dimension. Deterministic fractals Random and natural fractals See also * Fractal dimension * Hausdorff dimension * Scale invariance Notes and references Further reading * * * * External links The fractals on MathworldOther fractals on Paul Bourke's websiteFractals on mathcurve.com* [https://web.archive.org/web/20060923100014/http://library.thinkquest.org/26242/full/index.html Fractals unleashed] IFStile - software that computes the dimension of the boundary of self-affine tiles {{DEFAULTSORT:Fractals By Hausdorff Dimension Fractals, Hausdorff Dimension Fractal curves, Hausdorff Dimension Mathematics-related lists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithmically Random Sequence
Intuitively, an algorithmically random sequence (or random sequence) is a sequence of binary digits that appears random to any algorithm running on a (prefix-free or not) universal Turing machine. The notion can be applied analogously to sequences on any finite alphabet (e.g. decimal digits). Random sequences are key objects of study in algorithmic information theory. As different types of algorithms are sometimes considered, ranging from algorithms with specific bounds on their running time to algorithms which may ask questions of an oracle machine, there are different notions of randomness. The most common of these is known as Martin-Löf randomness (K-randomness or 1-randomness), but stronger and weaker forms of randomness also exist. When the term "algorithmically random" is used to refer to a particular single (finite or infinite) sequence without clarification, it is usually taken to mean "incompressible" or, in the case the sequence is infinite and prefix algorithmically r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cantor Space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space. Examples The Cantor set itself is a Cantor space. But the canonical example of a Cantor space is the countably infinite topological product of the discrete 2-point space . This is usually written as 2^\mathbb or 2ω (where 2 denotes the 2-element set with the discrete topology). A point in 2ω is an infinite binary sequence, that is a sequence which assumes only the values 0 or 1. Given such a sequence ''a''0, ''a''1, ''a''2,..., one can map it to the real number :\sum_^\infty \frac. This mapping gives a homeomorphism from 2ω onto the Cantor set, demonstrating that 2ω is indeed a Cantor space. Cantor spaces occur abundantly in real analysis. For example, they exist as subspaces in every perfect, complete metric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martingale (probability Theory)
In probability theory, a martingale is a sequence of random variables (i.e., a stochastic process) for which, at a particular time, the conditional expectation of the next value in the sequence is equal to the present value, regardless of all prior values. History Originally, '' martingale'' referred to a class of betting strategies that was popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins their stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double their bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, their probability of eventually flipping heads approaches 1, which makes the martingale betting strategy seem like a sure thing. However, the exponential growth of the bets eventually bankrupts its users due to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov Complexity
In algorithmic information theory (a subfield of computer science and mathematics), the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program (in a predetermined programming language) that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory. The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Cantor's diagonal argument, Gödel's incompleteness theorem, and Turing's halting problem. In particular, no program ''P'' computing a lower bound for each text's Kolmogorov complexity can return a value essentially larger than ''P'''s own leng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractals
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called Affine geometry, affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they Scaling (geometry), scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |