|
EXPSPACE
In computational complexity theory, is the set of all decision problems solvable by a deterministic Turing machine in exponential space, i.e., in O(2^) space, where p(n) is a polynomial function of n. Some authors restrict p(n) to be a linear function, but most authors instead call the resulting class . If we use a nondeterministic machine instead, we get the class , which is equal to by Savitch's theorem. A decision problem is if it is in , and every problem in has a polynomial-time many-one reduction to it. In other words, there is a polynomial-time algorithm that transforms instances of one to instances of the other with the same answer. problems might be thought of as the hardest problems in . is a strict superset of , , and . It contains and is believed to strictly contain it, but this is unproven. Formal definition In terms of and , :\mathsf = \bigcup_ \mathsf\left(2^\right) = \bigcup_ \mathsf\left(2^\right) Examples of problems Formal languages An examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
EXPTIME
In computational complexity theory, the complexity class EXPTIME (sometimes called EXP or DEXPTIME) is the set of all decision problems that are solvable by a deterministic Turing machine in exponential time, i.e., in O(2''p''(''n'')) time, where ''p''(''n'') is a polynomial function of ''n''. EXPTIME is one intuitive class in an exponential hierarchy of complexity classes with increasingly more complex oracles or quantifier alternations. For example, the class 2-EXPTIME is defined similarly to EXPTIME but with a doubly exponential time bound. This can be generalized to higher and higher time bounds. EXPTIME can also be reformulated as the space class APSPACE, the set of all problems that can be solved by an alternating Turing machine in polynomial space. EXPTIME relates to the other basic time and space complexity classes in the following way: P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME ⊆ EXPSPACE. Furthermore, by the time hierarchy theorem and the space hiera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of logic gate, gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems that can be solved by a Turing machine using a polynomial amount of space. Formal definition If we denote by SPACE(''f''(''n'')), the set of all problems that can be solved by Turing machines using ''O''(''f''(''n'')) space for some function ''f'' of the input size ''n'', then we can define PSPACE formally asArora & Barak (2009) p.81 :\mathsf = \bigcup_ \mathsf(n^k). It turns out that allowing the Turing machine to be nondeterministic does not add any extra power. Because of Savitch's theorem,Arora & Barak (2009) p.85 NPSPACE is equivalent to PSPACE, essentially because a deterministic Turing machine can simulate a nondeterministic Turing machine without needing much more space (even though it may use much more time).Arora & Barak (2009) p.86 Also, the complements of all problems in PSPACE are also in PSPACE, meaning that co-PSPACE PSPACE. Relation among other classes The following re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
NSPACE
In computational complexity theory, non-deterministic space or NSPACE is the computational resource describing the memory space for a non-deterministic Turing machine. It is the non-deterministic counterpart of DSPACE. Complexity classes The measure NSPACE is used to define the complexity class whose solutions can be determined by a non-deterministic Turing machine. The complexity class NSPACE(''f''(''n'')) is the set of decision problems that can be solved by a non-deterministic Turing machine, ''M'', using space ''O''(''f''(''n'')), where ''n'' is the length of the input. Several important complexity classes can be defined in terms of ''NSPACE''. These include: * REG = DSPACE(''O''(1)) = NSPACE(''O''(1)), where REG is the class of regular languages (nondeterminism does not add power in constant space). * NL = NSPACE(''O''(log ''n'')) * CSL = NSPACE(''O''(''n'')), where CSL is the class of context-sensitive languages. * PSPACE = NPSPACE = \bigcup_ \mathsf(n^k) * EXPSPA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Reachability Problem
Reachability is a fundamental problem which can be formulated as follows: ''Given a computational system with a set of allowed rules or transformations, decide whether a certain state of a system is reachable from a given initial state of the system.'' It appears in several different contexts: finite- and infinite-state concurrent systems, cellular automata and Petri nets, program analysis, discrete and continuous systems, time critical systems, hybrid systems, rewriting systems, probabilistic and parametric systems, and open systems modelled as games. Variants of the reachability problem may result from additional constraints on the initial or final states, specific requirement for reachability paths as well as for iterative reachability or changing the questions into analysis of winning strategies in infinite games or unavoidability of some dynamics. Typically, for a fixed system description given in some form (reduction rules, systems of equations, logical formulas, et ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
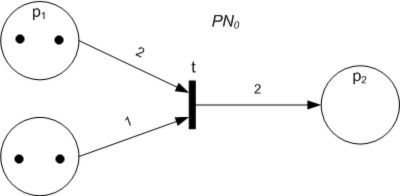
Petri Nets
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
NP (complexity)
In computational complexity theory, NP (nondeterministic polynomial time) is a complexity class used to classify decision problems. NP is the Set (mathematics), set of decision problems for which the Computational complexity theory#Problem instances, problem instances, where the answer is "yes", have mathematical proof, proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.''Polynomial time'' refers to how quickly the number of operations needed by an algorithm, relative to the size of the problem, grows. It is therefore a measure of efficiency of an algorithm. * NP is the set of decision problems ''solvable'' in polynomial time by a nondeterministic Turing machine. * NP is the set of decision problems ''verifiable'' in polynomial time by a deterministic Turing machine. The first definition is the basis for the abbreviation NP; "Nondeterministic alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Decision Problem
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question on a set of input values. An example of a decision problem is deciding whether a given natural number is prime. Another example is the problem, "given two numbers ''x'' and ''y'', does ''x'' evenly divide ''y''?" A decision procedure for a decision problem is an algorithmic method that answers the yes-no question on all inputs, and a decision problem is called decidable if there is a decision procedure for it. For example, the decision problem "given two numbers ''x'' and ''y'', does ''x'' evenly divide ''y''?" is decidable since there is a decision procedure called long division that gives the steps for determining whether ''x'' evenly divides ''y'' and the correct answer, ''YES'' or ''NO'', accordingly. Some of the most important problems in mathematics are undecidable, e.g. the halting problem. The field of computational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quanta Magazine
''Quanta Magazine'' is an editorially independent online publication of the Simons Foundation covering developments in physics, mathematics, biology and computer science. History ''Quanta Magazine'' was initially launched as ''Simons Science News'' in October 2012, but it was renamed to its current title in July 2013. It was founded by the former ''New York Times'' journalist Thomas Lin, who was the magazine's editor-in-chief until 2024. The two deputy editors are John Rennie and Michael Moyer, formerly of ''Scientific American'', and the art director is Samuel Velasco. In 2024, Samir Patel became the magazine's second editor in chief. Content The articles in the magazine are freely available to read online. ''Scientific American'', ''Wired'', ''The Atlantic'', and ''The Washington Post'', as well as international science publications like '' Spektrum der Wissenschaft'', have reprinted articles from the magazine. In November 2018, MIT Press The MIT Press is the uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ackermann Function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total function, total computable function that is not Primitive recursive function, primitive recursive. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. After Ackermann's publication of his function (which had three non-negative integer arguments), many authors modified it to suit various purposes, so that today "the Ackermann function" may refer to any of numerous variants of the original function. One common version is the two-argument Ackermann–Péter function developed by Rózsa Péter and Raphael Robinson. This function is defined from the recurrence relation \operatorname(m+1, n+1) = \operatorname(m, \operatorname(m+1, n)) with appropriate Base case (recursion), base cases. Its value grows very rapidly; for example, \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nonelementary Problem
In computational complexity theory, a nonelementary problem is a problem that is not a member of the class ELEMENTARY. As a class it is sometimes denoted as NONELEMENTARY. Examples of nonelementary problems that are nevertheless decidable include: * the problem of regular expression equivalence with complementation * the decision problem for monadic second-order logic over trees (see S2S) * the decision problem for term algebras * satisfiability of W. V. O. Quine's fluted fragment of first-order logic * deciding β-convertibility of two closed terms in typed lambda calculus * reachability in vector addition systems; it is Ackermann-complete. * reachability in Petri nets A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite grap ...; it is Ackermann-complete. References Complexity clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Temporal Logic
In logic, linear temporal logic or linear-time temporal logic (LTL) is a modal logic, modal temporal logic with modalities referring to time. In LTL, one can encode formula (logic), formulae about the future of path (graph theory), paths, e.g., a condition will eventually be true, a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which additionally allows branching time and quantifier (logic), quantifiers. LTL is sometimes called propositional temporal logic (PTL). In terms of expressive power (computer science), expressive power, LTL is a fragment of first-order logic. LTL was first proposed for the formal verification of computer programs by Amir Pnueli in 1977. Syntax LTL is built up from a finite set of propositional variables ''AP'', the logical connective, logical operators ¬ and ∨, and the Temporal logic, temporal modal operators X (some literature uses O or N) and U. Formally, the set of LTL formulas over ''AP'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |