|
E-shaped
Many shapes have metaphorical names, i.e., their names are metaphors: these shapes are named after a most common object that has it. For example, "U-shape" is a shape that resembles the letter U, a bell-shaped curve has the shape of the vertical cross-section of a bell, etc. These terms may variously refer to objects, their cross sections or projections. Types of shapes Some of these names are "classical terms", i.e., words of Latin or Ancient Greek etymology. Others are English language constructs (although the base words may have non-English etymology). In some disciplines, where shapes of subjects in question are a very important consideration, the shape naming may be quite elaborate, see, e.g., the taxonomy of shapes of plant leaves in botany. * Astroid * Aquiline, shaped like an eagle's beak (as in a Roman nose) * Bell-shaped curve * Biconic shape, a shape in a way opposite to the hourglass: it is based on two oppositely oriented cones or truncated cones wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian 2d
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymous adjective ''Gaussian'' is pronounced . Mathematics Algebra and linear algebra Geometry and differential geometry Number theory Cyclotomic fields *Gaussian period *Gaussian rational *Gauss sum, an exponential sum over Dirichlet characters **Elliptic Gauss sum, an analog of a Gauss sum ** Quadratic Gauss sum Analysis, numerical analysis, vector calculus and calculus of variations Complex analysis and convex analysis * Gauss–Lucas theorem *Gauss's continued fraction, an analytic continued fraction derived from the hypergeometric functions * Gauss's criterion – described oEncyclopedia of Mathematics* Gauss's hypergeometric theorem, an identity on hypergeometric series * Gauss plane Statistics * Gauss–K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Botany
Botany, also called plant science (or plant sciences), plant biology or phytology, is the science of plant life and a branch of biology. A botanist, plant scientist or phytologist is a scientist who specialises in this field. The term "botany" comes from the Ancient Greek word (') meaning " pasture", "herbs" " grass", or "fodder"; is in turn derived from (), "to feed" or "to graze". Traditionally, botany has also included the study of fungi and algae by mycologists and phycologists respectively, with the study of these three groups of organisms remaining within the sphere of interest of the International Botanical Congress. Nowadays, botanists (in the strict sense) study approximately 410,000 species of land plants of which some 391,000 species are vascular plants (including approximately 369,000 species of flowering plants), and approximately 20,000 are bryophytes. Botany originated in prehistory as herbalism with the efforts of early humans to identify – a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egg-shaped
An oval () is a closed curve in a plane which resembles the outline of an egg. The term is not very specific, but in some areas (projective geometry, technical drawing, etc.) it is given a more precise definition, which may include either one or two axes of symmetry of an ellipse. In common English, the term is used in a broader sense: any shape which reminds one of an egg. The three-dimensional version of an oval is called an ovoid. Oval in geometry The term oval when used to describe curves in geometry is not well-defined, except in the context of projective geometry. Many distinct curves are commonly called ovals or are said to have an "oval shape". Generally, to be called an oval, a plane curve should ''resemble'' the outline of an egg or an ellipse. In particular, these are common traits of ovals: * they are differentiable (smooth-looking), simple (not self-intersecting), convex, closed, plane curves; * their shape does not depart much from that of an ellipse, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a '' toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a ''solid torus'', which is form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pine Cone
A conifer cone (in formal botanical usage: strobilus, plural strobili) is a seed-bearing organ on gymnosperm plants. It is usually woody, ovoid to globular, including scales and bracts arranged around a central axis, especially in conifers and cycads. The cone of Pinophyta (conifer clade) contains the reproductive structures. The woody cone is the female cone, which produces seeds. The male cone, which produces pollen, is usually herbaceous and much less conspicuous even at full maturity. The name "cone" derives from Greek ''konos'' (pine cone), which also gave name to the geometric cone. The individual plates of a cone are known as ''scales''. The ''umbo'' of a conifer cone refers to the first year's growth of a seed scale on the cone, showing up as a protuberance at the end of the two-year-old scale. The male cone (microstrobilus or pollen cone) is structurally similar across all conifers, differing only in small ways (mostly in scale arrangement) from species to species ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
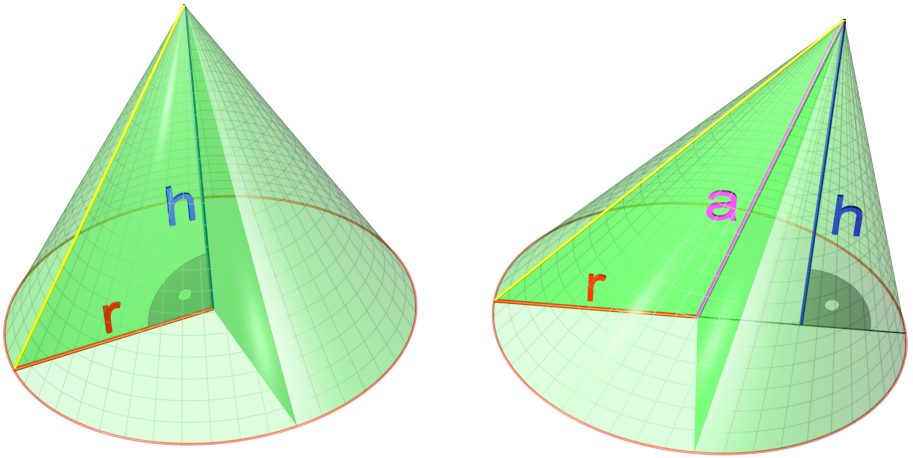
Cone (geometry)
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of hal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly Curve (algebraic)
In mathematics, the algebraic butterfly curve is a plane algebraic curve of degree six, given by the equation :x^6 + y^6 = x^2. The butterfly curve has a single singularity with delta invariant three, which means it is a curve of genus seven. The only plane curves of genus seven are singular, since seven is not a triangular number, and the minimum degree for such a curve is six. The butterfly curve has branching number and multiplicity two, and hence the singularity link has two components, pictured at right. The area of the algebraic butterfly curve is given by (with gamma function \Gamma) :4 \cdot \int_0^1 (x^2 - x^6)^ dx = \frac \approx 2.804, and its arc length ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services ... ''s'' by :s \approx 9.017. See also * Butterfly curve (t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bow Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ramjet
A ramjet, or athodyd (aero thermodynamic duct), is a form of airbreathing jet engine that uses the forward motion of the engine to produce thrust. Since it produces no thrust when stationary (no ram air) ramjet-powered vehicles require an assisted take-off like a rocket assist to accelerate it to a speed where it begins to produce thrust. Ramjets work most efficiently at supersonic speeds around and can operate up to speeds of . Ramjets can be particularly useful in applications requiring a small and simple mechanism for high-speed use, such as missiles. The US, Canada, and UK had widespread ramjet powered missile defenses during the 1960s onward, such as the CIM-10 Bomarc and Bloodhound. Weapon designers are looking to use ramjet technology in artillery shells to give added range; a 120 mm mortar shell, if assisted by a ramjet, is thought to be able to attain a range of . They have also been used successfully, though not efficiently, as tip jets on the ends of hel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inlet Cone
Inlet cones (sometimes called shock cones or inlet centerbodies) are a component of some Sound barrier, supersonic aircraft and missiles. They are primarily used on ramjets, such as the D-21 Tagboard and Lockheed X-7. Some turbojet aircraft including the Su-7, MiG-21, English Electric Lightning, and SR-71 also use an inlet cone. Purpose An inlet cone, as part of an Oswatitsch-type inlet used on a supersonic aircraft or missile, is the surface on which supersonic ram compression for a gas turbine engine or ramjet combustor takes place through oblique shock waves. Slowing the air to low supersonic speeds using a cone minimizes loss in total pressure (increases pressure recovery). Also, the cone, together with the inlet cowl lip, determine the area which regulates the flow entering the inlet. If the flow is more than that required by the engine then shock position instability(buzz) can occur. If less than that required then the pressure recovery is lower which reduces engine thrust. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Reentry
Atmospheric entry is the movement of an object from outer space into and through the gases of an atmosphere of a planet, dwarf planet, or natural satellite. There are two main types of atmospheric entry: ''uncontrolled entry'', such as the entry of astronomical objects, space debris, or bolides; and ''controlled entry'' (or ''reentry'') of a spacecraft capable of being navigated or following a predetermined course. Technologies and procedures allowing the controlled atmospheric ''entry, descent, and landing'' of spacecraft are collectively termed as ''EDL''. Objects entering an atmosphere experience atmospheric drag, which puts mechanical stress on the object, and aerodynamic heating—caused mostly by compression of the air in front of the object, but also by drag. These forces can cause loss of mass ( ablation) or even complete disintegration of smaller objects, and objects with lower compressive strength can explode. Crewed space vehicles must be slowed to subsonic s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Cone
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal, the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise it is an oblique frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism (possibly oblique or/and with irregular bases). In computer graphics, the viewing frustum is the three-dimensional region which is visible on the screen. It is formed by a clipped pyramid; in particular, '' frustum culling'' is a method of hidden surface determination. In the aerospace industry, a frustum is the fairing between two stages of a multistage rocket (such as the Saturn V), which is shaped like a truncated cone. Elements, special cases, and related concepts A frustum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |