|
Dissipative System
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter. A tornado may be thought of as a dissipative system. Dissipative systems stand in contrast to conservative systems. A dissipative structure is a dissipative system that has a dynamical regime that is in some sense in a reproducible steady state. This reproducible steady state may be reached by natural evolution of the system, by artifice, or by a combination of these two. Overview A dissipative structure is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. Examples in everyday life include convection, turbulent flow, cyclones, hurricanes and living organisms. Less common examples include lasers, B├®nard cells, droplet cluster, and the BelousovŌ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open System (systems Theory)
An open system is a system that has external interactions. Such interactions can take the form of information, energy, or material transfers into or out of the system boundary, depending on the discipline which defines the concept. An open system is contrasted with the concept of an isolated system which exchanges neither energy, matter, nor information with its environment. An open system is also known as a flow system. The concept of an open system was formalized within a framework that enabled one to interrelate the theory of the organism, thermodynamics, and evolutionary theory. This concept was expanded upon with the advent of information theory and subsequently systems theory. Today the concept has its applications in the natural and social sciences. In the natural sciences an open system is one whose border is permeable to both energy and mass. By contrast, a closed system is permeable to energy but not to matter. The definition of an open system assumes that there are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Droplet Cluster
Droplet cluster is a self-assembled levitating monolayer of microdroplets usually arranged into a hexagonally ordered structure over a locally heated thin (about 1 mm) layer of water. The droplet cluster is typologically similar to colloidal crystals. The phenomenon was observed for the first time in 2004, and it has been extensively studied after that. Growing condensing droplets with a typical diameter of 0.01 mm ŌĆō 0.2 mm levitate at an equilibrium height, where their weight is equilibrated by the drag force of the ascending air-vapor jet rising over the heated spot. At the same time, the droplets are dragged towards the center of the heated spot; however, they do not merge, forming an ordered hexagonal (densest packed) pattern due to an aerodynamic repulsive pressure force from gas flow between the droplets. The spot is usually heated by a laser beam or another source of heat to 60 ┬░C ŌĆō 95 ┬░C, although the phenomenon was observed also at tem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Onsager Reciprocal Relations
In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists. "Reciprocal relations" occur between different pairs of forces and flows in a variety of physical systems. For example, consider fluid systems described in terms of temperature, matter density, and pressure. In this class of systems, it is known that temperature differences lead to heat flows from the warmer to the colder parts of the system; similarly, pressure differences will lead to matter flow from high-pressure to low-pressure regions. What is remarkable is the observation that, when both pressure and temperature vary, temperature differences at constant pressure can cause matter flow (as in convection) and pressure differences at constant temperature can cause heat flow. Perhaps surprisingly, the heat flow per unit of pressure difference and the density (matter) flo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extremal Principles In Non-equilibrium Thermodynamics
Energy dissipation and entropy production extremal principles are ideas developed within non-equilibrium thermodynamics that attempt to predict the likely steady states and dynamical structures that a physical system might show. The search for extremum principles for non-equilibrium thermodynamics follows their successful use in other branches of physics.Ziegler, H., (1983). ''An Introduction to Thermomechanics'', North-Holland, Amsterdam, According to Kondepudi (2008), and to Grandy (2008),Grandy, W.T., Jr (2008). ''Entropy and the Time Evolution of Macroscopic Systems'', Oxford University Press, Oxford, . there is no general rule that provides an extremum principle that governs the evolution of a far-from-equilibrium system to a steady state. According to Glansdorff and Prigogine (1971, page 16), irreversible processes usually are not governed by global extremal principles because description of their evolution requires differential equations which are not self-adjoint, but loca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nobel Prize In Chemistry
) , image = Nobel Prize.png , alt = A golden medallion with an embossed image of a bearded man facing left in profile. To the left of the man is the text "ALFRŌĆó" then "NOBEL", and on the right, the text (smaller) "NATŌĆó" then "MDCCCXXXIII" above, followed by (smaller) "OBŌĆó" then "MDCCCXCVI" below. , awarded_for = Outstanding contributions in chemistry , presenter = Royal Swedish Academy of Sciences , location = Stockholm, Sweden , reward = 9 million SEK (2017) , year = 1901 , holder = Carolyn R. Bertozzi, Morten P. Meldal and Karl Barry Sharpless (2022) , most_awards = Frederick Sanger and Karl Barry Sharpless (2) , website nobelprize.org, previous = 2021 , year2=2022, main=2022, next=2023 The Nobel Prize in Chemistry is awarded annually by the Royal Swedish Academy of Sciences to scientists in the various fields of chemistry. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895, awarded for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ilya Prigogine
Viscount Ilya Romanovich Prigogine (; russian: ąśą╗čīčÅ╠ü ąĀąŠą╝ą░╠üąĮąŠą▓ąĖčć ą¤čĆąĖą│ąŠ╠üąČąĖąĮ; 28 May 2003) was a physical chemist and Nobel laureate noted for his work on dissipative structures, complex systems, and irreversibility. Biography Prigogine was born in Moscow a few months before the Russian Revolution of 1917, into a Jewish family. His father, Ruvim Abramovich Prigogine, was a chemical engineer at the Imperial Moscow Technical School; his mother, Yulia Vikhman, was a pianist. Because the family was critical of the new Soviet system, they left Russia in 1921. They first went to Germany and in 1929, to Belgium, where Prigogine received Belgian nationality in 1949. His brother Alexandre (1913ŌĆō1991) became an ornithologist. Prigogine studied chemistry at the Free University of Brussels, where in 1950, he became professor. In 1959, he was appointed director of the International Solvay Institute in Brussels, Belgium. In that year, he also started teaching at the U ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure Space
A measure space is a basic object of measure theory, a branch of mathematics that studies generalized notions of volumes. It contains an underlying set, the subsets of this set that are feasible for measuring (the -algebra) and the method that is used for measuring (the measure). One important example of a measure space is a probability space. A measurable space consists of the first two components without a specific measure. Definition A measure space is a triple (X, \mathcal A, \mu), where * X is a set * \mathcal A is a -algebra on the set X * \mu is a measure on (X, \mathcal) In other words, a measure space consists of a measurable space (X, \mathcal) together with a measure on it. Example Set X = \. The \sigma-algebra on finite sets such as the one above is usually the power set, which is the set of all subsets (of a given set) and is denoted by \wp(\cdot). Sticking with this convention, we set \mathcal = \wp(X) In this simple case, the power set can be written down ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hopf Decomposition
In mathematics, the Hopf decomposition, named after Eberhard Hopf, gives a canonical decomposition of a measure space (''X'', ╬╝) with respect to an invertible non-singular transformation ''T'':''X''ŌåÆ''X'', i.e. a transformation which with its inverse is measurable and carries null set In mathematical analysis, a null set N \subset \mathbb is a measurable set that has measure zero. This can be characterized as a set that can be covered by a countable union of intervals of arbitrarily small total length. The notion of null s ...s onto null sets. Up to null sets, ''X'' can be written as a disjoint union ''C'' ŌłÉ ''D'' of ''T''-invariant sets where the action of ''T'' on ''C'' is conservative and the action of ''T'' on ''D'' is dissipative. Thus, if Žä is the automorphism of ''A'' = LŌł×(''X'') induced by ''T'', there is a unique Žä-invariant projection ''p'' in ''A'' such that ''pA'' is conservative and ''(IŌĆōp)A'' is dissipative. Definitions *Wandering sets and dissipa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
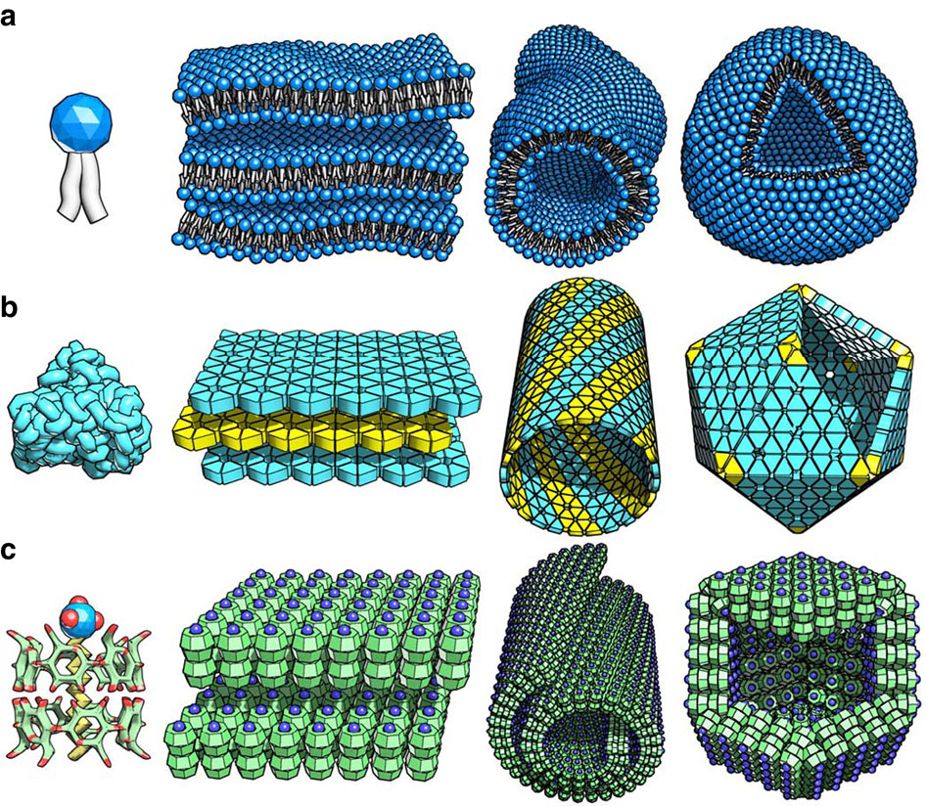
Self-assembly
Self-assembly is a process in which a disordered system of pre-existing components forms an organized structure or pattern as a consequence of specific, local interactions among the components themselves, without external direction. When the constitutive components are molecules, the process is termed molecular self-assembly. Self-assembly can be classified as either static or dynamic. In ''static'' self-assembly, the ordered state forms as a system approaches equilibrium, reducing its free energy. However, in ''dynamic'' self-assembly, patterns of pre-existing components organized by specific local interactions are not commonly described as "self-assembled" by scientists in the associated disciplines. These structures are better described as "self-organized", although these terms are often used interchangeably. Self-assembly in chemistry and materials science Self-assembly in the classic sense can be defined as ''the spontaneous and reversible organization of molec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Systems
A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, complex software and electronic systems, social and economic organizations (like cities), an ecosystem, a living cell, and ultimately the entire universe. Complex systems are systems whose behavior is intrinsically difficult to model due to the dependencies, competitions, relationships, or other types of interactions between their parts or between a given system and its environment. Systems that are "complex" have distinct properties that arise from these relationships, such as nonlinearity, emergence, spontaneous order, adaptation, and feedback loops, among others. Because such systems appear in a wide variety of fields, the commonalities among them have become the topic of their independent area of research. In many cases, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure (mathematics)
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of ├ēmile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |