|
Dynamic Epistemic Logic
Dynamic epistemic logic (DEL) is a logical framework dealing with knowledge and information change. Typically, DEL focuses on situations involving multiple agents and studies how their knowledge changes when events occur. These events can change factual properties of the actual world (they are called ''ontic events''): for example a red card is painted in blue. They can also bring about changes of knowledge without changing factual properties of the world (they are called ''epistemic events''): for example a card is revealed publicly (or privately) to be red. Originally, DEL focused on epistemic events. We only present in this entry some of the basic ideas of the original DEL framework; more details about DEL in general can be found in the references. Due to the nature of its object of study and its abstract approach, DEL is related and has applications to numerous research areas, such as computer science ( artificial intelligence), philosophy ( formal epistemology), economics (g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intelligent Agent
In artificial intelligence, an intelligent agent (IA) is anything which perceives its environment, takes actions autonomously in order to achieve goals, and may improve its performance with learning or may use knowledge. They may be simple or complex — a thermostat is considered an example of an intelligent agent, as is a human being, as is any system that meets the definition, such as a firm, a state, or a biome. Leading AI textbooks define "artificial intelligence" as the "study and design of intelligent agents", a definition that considers goal-directed behavior to be the essence of intelligence. Goal-directed agents are also described using a term borrowed from economics, " rational agent". An agent has an "objective function" that encapsulates all the IA's goals. Such an agent is designed to create and execute whatever plan will, upon completion, maximize the expected value of the objective function. For example, a reinforcement learning agent has a "reward functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hintikka
Kaarlo Jaakko Juhani Hintikka (12 January 1929 – 12 August 2015) was a Finnish philosopher and logician. Life and career Hintikka was born in Helsingin maalaiskunta (now Vantaa). In 1953, he received his doctorate from the University of Helsinki for a thesis entitled ''Distributive Normal Forms in the Calculus of Predicates''. He was a student of Georg Henrik von Wright. Hintikka was a Junior Fellow at Harvard University (1956-1969), and held several professorial appointments at the University of Helsinki, the Academy of Finland, Stanford University, Florida State University and finally Boston University from 1990 until his death. He was the prolific author or co-author of over 30 books and over 300 scholarly articles, Hintikka contributed to mathematical logic, philosophical logic, the philosophy of mathematics, epistemology, language theory, and the philosophy of science. His works have appeared in over nine languages. Hintikka edited the academic journal ''Synthese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Closure
In mathematics, the transitive closure of a binary relation on a set is the smallest relation on that contains and is transitive. For finite sets, "smallest" can be taken in its usual sense, of having the fewest related pairs; for infinite sets it is the unique minimal transitive superset of . For example, if is a set of airports and means "there is a direct flight from airport to airport " (for and in ), then the transitive closure of on is the relation such that means "it is possible to fly from to in one or more flights". Informally, the ''transitive closure'' gives you the set of all places you can get to from any starting place. More formally, the transitive closure of a binary relation on a set is the transitive relation on set such that contains and is minimal; see . If the binary relation itself is transitive, then the transitive closure is that same binary relation; otherwise, the transitive closure is a different relation. Conversely, transit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truth Conditions
In semantics and pragmatics, a truth condition is the condition under which a sentence is true. For example, "It is snowing in Nebraska" is true precisely when it is snowing in Nebraska. Truth conditions of a sentence do not necessarily reflect current reality. They are merely the conditions under which the statement would be true. More formally, a truth condition makes for the truth of a sentence in an inductive definition of truth (for details, see the semantic theory of truth). Understood this way, truth conditions are theoretical entities. To illustrate with an example: suppose that, in a particular truth theoryField, H. (1972). Tarski's Theory of Truth. ''The Journal of Philosophy,'' ''69''(13), 347-375. which is a theory of truth where truth is somehow made acceptable despite semantic terms as close as possible, the word "Nixon" refers to Richard M. Nixon, and "is alive" is associated with the set of currently living things. Then one way of representing the truth condit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over Set (mathematics), sets and is a new set of ordered pairs consisting of elements in and in . It is a generalization of the more widely understood idea of a unary function. It encodes the common concept of relation: an element is ''related'' to an element , if and only if the pair belongs to the set of ordered pairs that defines the ''binary relation''. A binary relation is the most studied special case of an Finitary relation, -ary relation over sets , which is a subset of the Cartesian product X_1 \times \cdots \times X_n. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime is related to each integer that is a Divisibility, multiple of , but not to an integer that is not a multiple of . In this relation, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
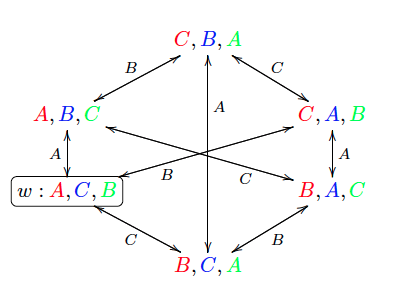
Kripke Model
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributed Systems
A distributed system is a system whose components are located on different networked computers, which communicate and coordinate their actions by passing messages to one another from any system. Distributed computing is a field of computer science that studies distributed systems. The components of a distributed system interact with one another in order to achieve a common goal. Three significant challenges of distributed systems are: maintaining concurrency of components, overcoming the lack of a global clock, and managing the independent failure of components. When a component of one system fails, the entire system does not fail. Examples of distributed systems vary from SOA-based systems to massively multiplayer online games to peer-to-peer applications. A computer program that runs within a distributed system is called a distributed program, and ''distributed programming'' is the process of writing such programs. There are many different types of implementations for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Lewis (philosopher)
David Kellogg Lewis (September 28, 1941 – October 14, 2001) was an American philosopher who is widely regarded as one of the most important philosophers of the 20th century. Lewis taught briefly at UCLA and then at Princeton University from 1970 until his death. He is closely associated with Australia, whose philosophical community he visited almost annually for more than 30 years. Lewis made significant contributions in philosophy of mind, philosophy of probability, epistemology, philosophical logic, aesthetics, philosophy of mathematics, philosophy of time and philosophy of science. In most of these fields he is considered among the most important figures of recent decades. But Lewis is most famous for his work in metaphysics, philosophy of language and semantics, in which his books ''On the Plurality of Worlds'' (1986) and ''Counterfactuals'' (1973) are considered classics. His works on the logic and semantics of counterfactual conditionals are broadly used by philosop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Grammar
In formal language theory, a grammar (when the context is not given, often called a formal grammar for clarity) describes how to form strings from a language's alphabet that are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language. Formal language theory, the discipline that studies formal grammars and languages, is a branch of applied mathematics. Its applications are found in theoretical computer science, theoretical linguistics, formal semantics, mathematical logic, and other areas. A formal grammar is a set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a " recognizer"—a function in computing tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributed Knowledge
In multi-agent system research, distributed knowledge is all the knowledge that a community of agents possesses and might apply in solving a problem. Distributed knowledge is approximately what "a wise man knows" or what someone who has complete knowledge of what each member of the community knows knows. Distributed knowledge might also be called the aggregate knowledge of a community, as it represents all the knowledge that a community might bring to bear to solve a problem. Other related phrasings include cumulative knowledge, collective knowledge or pooled knowledge. Distributed knowledge is the union of all the knowledge of individuals in a community of agents. Distributed knowledge differs from the concept of Wisdom of the crowd, in that the latter is concerned with opinions, not knowledge. Wisdom of the crowd is the emergent opinion arising from multiple actors. It is not the union of all the knowledge of these actors, it does not necessarily include the contribution of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |