|
Duplication Matrix
In mathematics, especially in linear algebra and matrix theory, the duplication matrix and the elimination matrix are linear transformations used for transforming half-vectorizations of matrices into vectorizations or (respectively) vice versa. Duplication matrix The duplication matrix D_n is the unique n^2 \times \frac matrix which, for any n \times n symmetric matrix A , transforms \mathrm(A) into \mathrm(A): : D_n \mathrm(A) = \mathrm(A). For the 2 \times 2 symmetric matrix A=\left begin a & b \\ b & d \end\right/math>, this transformation reads : D_n \mathrm(A) = \mathrm(A) \implies \begin 1&0&0 \\ 0&1&0 \\ 0&1&0 \\ 0&0&1 \end \begin a \\ b \\ d \end = \begin a \\ b \\ b \\ d \end The explicit formula for calculating the duplication matrix for a n \times n matrix is: D^T_n = \sum \limits_ u_ (\mathrmT_)^T Where: * u_ is a unit vector of order \frac n (n+1) having the value 1 in the position (j-1)n+i - \fracj(j-1) and 0 elsewhere; * T_ is a n \times n matrix wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the linear ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
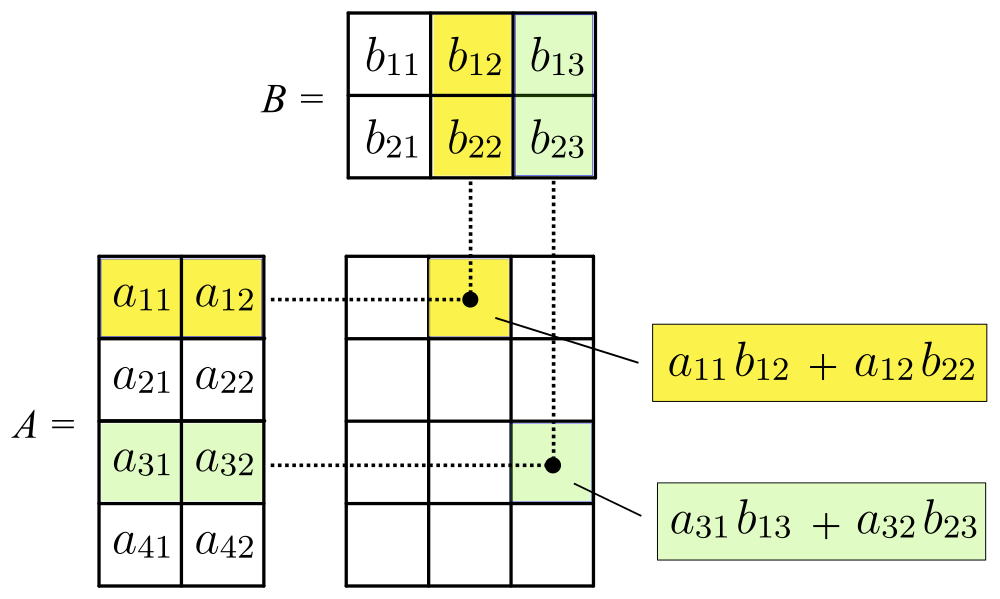
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) ''endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vectorization (mathematics)
In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector. Specifically, the vectorization of a matrix ''A'', denoted vec(''A''), is the column vector obtained by stacking the columns of the matrix ''A'' on top of one another: :\operatorname(A) = _, \ldots, a_, a_, \ldots, a_, \ldots, a_, \ldots, a_\mathrm Here, a_ represents A(i,j) and the superscript ^\mathrm denotes the transpose. Vectorization expresses, through coordinates, the isomorphism \mathbf^ := \mathbf^m \otimes \mathbf^n \cong \mathbf^ between these (i.e., of matrices and vectors) as vector spaces. For example, for the 2×2 matrix A = \begin a & b \\ c & d \end, the vectorization is \operatorname(A) = \begin a \\ c \\ b \\ d \end. The connection between the vectorization of ''A'' and the vectorization of its transpose is given by the commutation matrix. Compatibility with Kronecker products The vector ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Armadillo (C++ Library)
Armadillos (meaning "little armored ones" in Spanish) are New World placental mammals in the order Cingulata. The Chlamyphoridae and Dasypodidae are the only surviving families in the order, which is part of the superorder Xenarthra, along with the anteaters and sloths. Nine extinct genera and 21 extant species of armadillo have been described, some of which are distinguished by the number of bands on their armor. All species are native to the Americas, where they inhabit a variety of different environments. Armadillos are characterized by a leathery armor shell and long, sharp claws for digging. They have short legs, but can move quite quickly. The average length of an armadillo is about , including its tail. The giant armadillo grows up to and weighs up to , while the pink fairy armadillo has a length of only . When threatened by a predator, ''Tolypeutes'' species frequently roll up into a ball; they are the only species of armadillo capable of this. Etymology The word ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrices
Matrix most commonly refers to: * ''The Matrix'' (franchise), an American media franchise ** ''The Matrix'', a 1999 science-fiction action film ** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchise) * Matrix (mathematics), a rectangular array of numbers, symbols or expressions Matrix (or its plural form matrices) may also refer to: Science and mathematics * Matrix (mathematics), algebraic structure, extension of vector into 2 dimensions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Arts and entertainment Fictional entities * Matrix (comics), two comic book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
