|
Discrete-time Proportional Hazards
In survival analysis, hazard rate models are widely used to model duration data in a wide range of disciplines, from bio-statistics to economics. Grouped duration data are widespread in many applications. Unemployment durations are typically measured over weeks or months and these time intervals may be considered too large for continuous approximations to hold. In this case, we will typically have grouping points t_, where a=1,...,A.. Models allow for time-invariant and time-variant covariates, but the latter require stronger assumptions in terms of exogeneity. The discrete-time hazard function can be written as: \lambda_(t_, \chi)= Pr(t_\leqslant T |
Survival Analysis
Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory, reliability analysis or reliability engineering in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival? To answer such questions, it is necessary to define "lifetime". In the case of biological survival, death is unambiguous, but for mechanical reliability, failure may not be well-defined, for there may well be mechanical systems in which failure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-invariant System
In control theory, a time-invariant (TI) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends ''only'' indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system". Mathematically speaking, "time-invariance" of a system is the following property: :''Given a system with a time-dependent output function , and a time-dependent input function , the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship betwe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-variant System
A time-variant system is a system whose output response depends on moment of observation as well as moment of input signal application. In other words, a time delay or time advance of input not only shifts the output signal in time but also changes other parameters and behavior. Time variant systems respond differently to the same input at different times. The opposite is true for time invariant systems (TIV). Overview There are many well developed techniques for dealing with the response of linear time invariant systems, such as Laplace and Fourier transforms. However, these techniques are not strictly valid for time-varying systems. A system undergoing slow time variation in comparison to its time constants can usually be considered to be time invariant: they are close to time invariant on a small scale. An example of this is the aging and wear of electronic components, which happens on a scale of years, and thus does not result in any behaviour qualitatively different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariate
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the output is ; the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exogeneity
In a variety of contexts, exogeny or exogeneity () is the fact of an action or object originating externally. It is the opposite of endogeneity or endogeny, the fact of being influenced from within a system. Economics In an economic model, an exogenous change is one that comes from outside the model and is unexplained by the model. Such changes of an economic model from outside factors can include the influence of technology, in which this had previously been noted as an exogenous factor, but has rather been noted as a factor that can depict economic forces as a whole. In economic sociology, Project IDEA (Interdisciplinary Dimensions of Economic Analysis) gave notion to understanding the exogenous factors that play a role within economic theory. Developed from the International Social Science Council (ISSC) in the year of 1982, Project IDEA was founded to gather ideas from economists and sociologists in order to conceptualize what economic sociology incorporates, as they hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Survival Function
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive past a certain time. The survival function is also known as the survivor function or reliability function. The term ''reliability function'' is common in engineering while the term ''survival function'' is used in a broader range of applications, including human mortality. The survival function is the complementary cumulative distribution function of the lifetime. Sometimes complementary cumulative distribution functions are called survival functions in general. Definition Let the lifetime T be a continuous random variable describing the time to failure. If T has cumulative distribution function F(t) and probability density function f(t) on the interval [0,\infty), then the ''survival function'' or ''reliability function'' is: S(t) = P(T > t) = 1-F(t) = 1 - \int_0^t f(u)\,du Examples of survival functions The graphs below show examples of hypot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood Function
A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability of seeing that data under different parameter values of the model. It is constructed from the joint probability distribution of the random variable that (presumably) generated the observations. When evaluated on the actual data points, it becomes a function solely of the model parameters. In maximum likelihood estimation, the argument that maximizes the likelihood function serves as a point estimate for the unknown parameter, while the Fisher information (often approximated by the likelihood's Hessian matrix at the maximum) gives an indication of the estimate's precision. In contrast, in Bayesian statistics, the estimate of interest is the ''converse'' of the likelihood, the so-called posterior probability of the parameter given the observed data, which is calculated via Bayes' rule. Definition The likelihood function, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Model
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters. Definition A statistical model is a collection of probability distributions on some sample space. We assume that the collection, , is indexed by some set . The set is called the parameter set or, more commonly, the parameter space. For each , let denote the corresponding member of the collection; so is a cumulative distribution function. Then a statistical model can be written as : \mathcal = \big\. The model is a parametric model if for some positive integer . When the model consists of absolutely continuous distributions, it is often specified in terms of corresponding probability density functions: : \mathcal = \big\. Examples * The Poisson family of distributions is parametrized by a single number : : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
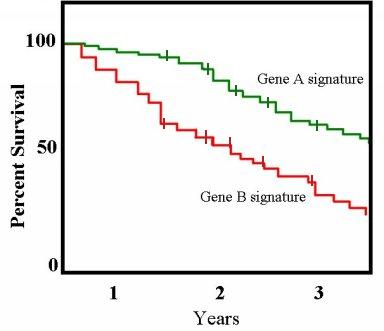
Kaplan–Meier Estimator
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the ''Journal of the American Statistical Association''. The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited more than 34,000 times since its publication in 1958. The estimator of the survival function S(t) (the probability that life is longer than t) is given by: : \widehat S(t) = \prod\limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Choice Model
In economics, discrete choice models, or qualitative choice models, describe, explain, and predict choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Such choices contrast with standard consumption models in which the quantity of each good consumed is assumed to be a continuous variable. In the continuous case, calculus methods (e.g. first-order conditions) can be used to determine the optimum amount chosen, and demand can be modeled empirically using regression analysis. On the other hand, discrete choice analysis examines situations in which the potential outcomes are discrete, such that the optimum is not characterized by standard first-order conditions. Thus, instead of examining "how much" as in problems with continuous choice variables, discrete choice analysis examines "which one". However, discrete choice analysis can also be used to examine the chosen quantity when only a few distinc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |