|
Discrepancy Theory
In mathematics, discrepancy theory describes the deviation of a situation from the state one would like it to be in. It is also called the theory of irregularities of distribution. This refers to the theme of ''classical'' discrepancy theory, namely distributing points in some space such that they are evenly distributed with respect to some (mostly geometrically defined) subsets. The discrepancy (irregularity) measures how far a given distribution deviates from an ideal one. Discrepancy theory can be described as the study of inevitable irregularities of distributions, in measure-theoretic and combinatorial settings. Just as Ramsey theory elucidates the impossibility of total disorder, discrepancy theory studies the deviations from total uniformity. A significant event in the history of discrepancy theory was the 1916 paper of Weyl on the uniform distribution of sequences in the unit interval. __NOTOC__ Theorems Discrepancy theory is based on the following classic theorems: * T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure Theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heilbronn Triangle Problem
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown. Definition The Heilbronn triangle problem concerns the placement of n points within a shape in the plane, such as the unit square or the unit disk, for a given Each triple of points form the three vertices of a triangle, and among these triangles, the problem concerns the smallest triangle, as measured by area. Different placements of points will have different smallest triangles, and the problem asks: how should n points be placed to maximize the area of the smallest More formally, the shape may be assumed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unsolved Problems In Mathematics
Many mathematical problems have been stated but not yet solved. These problems come from many areas of mathematics, such as theoretical physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential equations. Some problems belong to more than one discipline and are studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and some lists of unsolved problems, such as the Millennium Prize Problems, receive considerable attention. This list is a composite of notable unsolved problems mentioned in previously published lists, including but not limited to lists considered authoritative. Although this list may never be comprehensive, the problems listed here vary widely in both difficulty and importance. Lists of unsolved problems in mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diophantine Approximation
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria. The first problem was to know how well a real number can be approximated by rational numbers. For this problem, a rational number ''a''/''b'' is a "good" approximation of a real number ''α'' if the absolute value of the difference between ''a''/''b'' and ''α'' may not decrease if ''a''/''b'' is replaced by another rational number with a smaller denominator. This problem was solved during the 18th century by means of continued fractions. Knowing the "best" approximations of a given number, the main problem of the field is to find sharp upper and lower bounds of the above difference, expressed as a function of the denominator. It appears that these bounds depend on the nature of the real numbers to be approximated: the lower bound for the approximation of a rational number by another rational number is larger than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrepancy Of Hypergraphs
Discrepancy of hypergraphs is an area of discrepancy theory. Definitions In the classical setting, we aim at partitioning the vertices of a hypergraph \mathcal=(V, \mathcal) into two classes in such a way that ideally each hyperedge contains the same number of vertices in both classes. A partition into two classes can be represented by a coloring \chi \colon V \rightarrow \. We call −1 and +1 ''colors''. The color-classes \chi^(-1) and \chi^(+1) form the corresponding partition. For a hyperedge E \in \mathcal, set :\chi(E) := \sum_ \chi(v). The ''discrepancy of \mathcal with respect to \chi'' and the ''discrepancy of \mathcal'' are defined by :\operatorname(\mathcal,\chi) := \; \max_ , \chi(E), , :\operatorname(\mathcal) := \min_ \operatorname(\mathcal, \chi). These notions as well as the term 'discrepancy' seem to have appeared for the first time in a paper of Beck.J. Beck: "Roth's estimate of the discrepancy of integer sequences is nearly sharp", page 319-325. Combinatorica, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
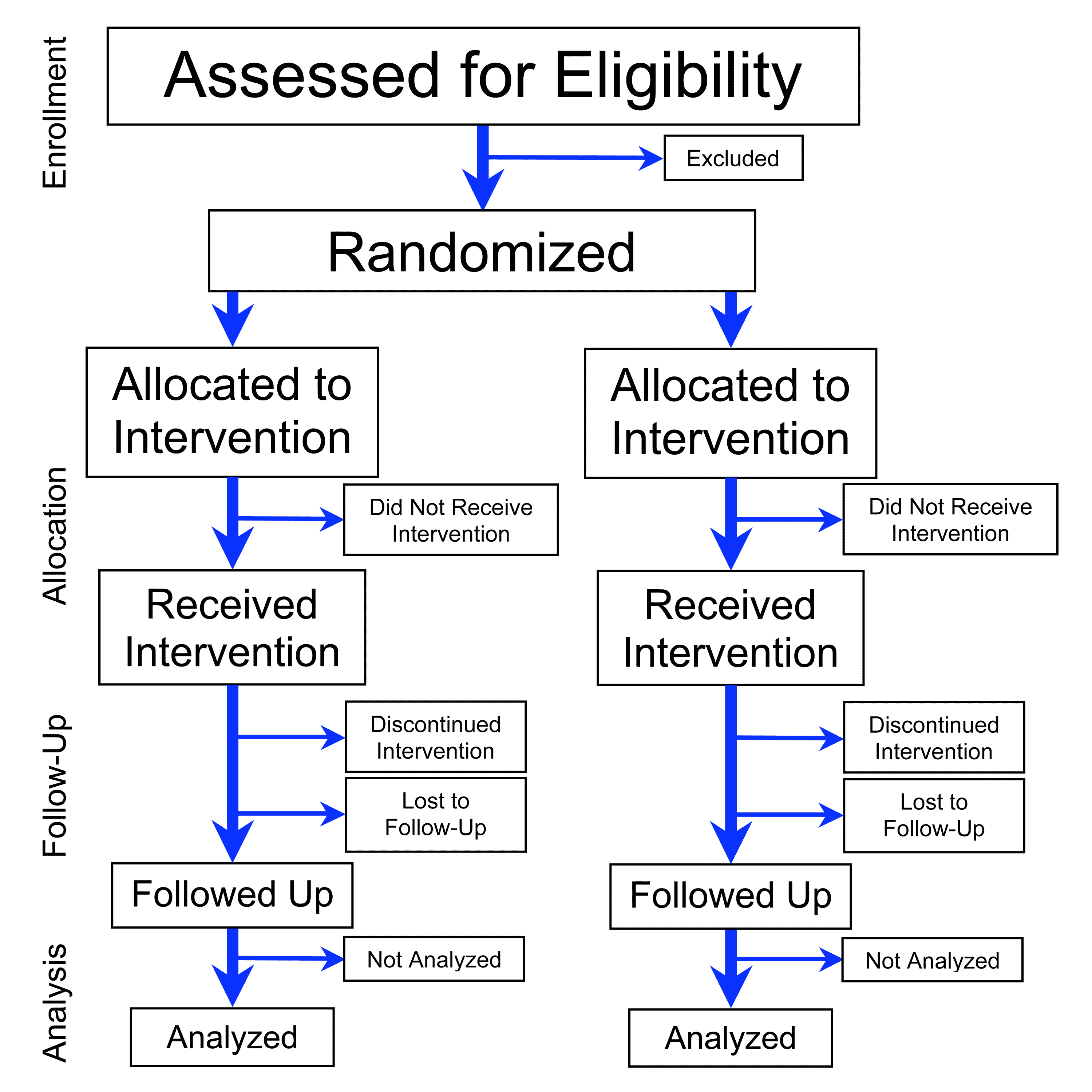
Randomized Controlled Trial
A randomized controlled trial (or randomized control trial; RCT) is a form of scientific experiment used to control factors not under direct experimental control. Examples of RCTs are clinical trials that compare the effects of drugs, surgical techniques, medical devices, diagnostic procedures or other medical treatments. Participants who enroll in RCTs differ from one another in known and unknown ways that can influence study outcomes, and yet cannot be directly controlled. By Random assignment, randomly allocating participants among compared treatments, an RCT enables ''statistical control'' over these influences. Provided it is designed well, conducted properly, and enrolls enough participants, an RCT may achieve sufficient control over these confounding factors to deliver a useful comparison of the treatments studied. Definition and examples An RCT in clinical research typically compares a proposed new treatment against an existing Standard of care#Medical standard of care, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halftone
Halftone is the reprographic Reprography (a portmanteau of ''reproduction'' and ''photography'') is the reproduction of graphics through mechanical or electrical means, such as photography or xerography. Reprography is commonly used in catalogs and archives, as well as in th ... technique that simulates continuous-tone imagery through the use of dots, varying either in size or in spacing, thus generating a gradient-like effect.Campbell, Alastair. The Designer's Lexicon. ©2000 Chronicle, San Francisco. "Halftone" can also be used to refer specifically to the image that is produced by this process. Where continuous-tone imagery contains an infinite range of colors or greys, the halftone process reduces visual reproductions to an image that is printed with only one color of ink, in dots of differing size (pulse-width modulation) or spacing (frequency modulation) or both. This reproduction relies on a basic optical illusion: when the halftone dots are small, the human eye inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divide-and-conquer Algorithm
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. The divide-and-conquer technique is the basis of efficient algorithms for many problems, such as sorting (e.g., quicksort, merge sort), multiplying large numbers (e.g., the Karatsuba algorithm), finding the closest pair of points, syntactic analysis (e.g., top-down parsers), and computing the discrete Fourier transform (FFT). Designing efficient divide-and-conquer algorithms can be difficult. As in mathematical induction, it is often necessary to generalize the problem to make it amenable to a recursive solution. The correctness of a divide-and-conquer algorithm is usually proved by mathematical induction, and its computational cost is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
János Komlós (mathematician)
János Komlós (born 23 May 1942, in Budapest) is a Hungarian-American mathematician, working in probability theory and discrete mathematics. He has been a professor of mathematics at Rutgers University since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute of the Hungarian Academy of Sciences. Between 1984–1988 he worked at the University of California, San Diego. Notable results * He proved that every L1-bounded sequence of real functions contains a subsequence such that the arithmetic means of all its subsequences converge pointwise almost everywhere. In probabilistic terminology, the theorem is as follows. Let ξ1,ξ2,... be a sequence of random variables such that ''E'' ¾1''E'' ¾2... is bounded. Then there exist a subsequence ξ'1, ξ'2,... and a random variable β such that for each further subsequence η1,η2,... of ξ'0, ξ'1,... we have (η1+...+ηn)/n → β a.s. * With Miklós Ajtai and Endre Szemeréd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beck–Fiala Theorem
In mathematics, the Beck–Fiala theorem is a major theorem in discrepancy theory due to József Beck József Beck (Budapest, Hungary, February 14, 1952) is a Harold H. Martin Professor of Mathematics at Rutgers University. His contributions to combinatorics include the partial colouring lemma and the Beck–Fiala theorem in '' discrepancy th ... and Tibor Fiala. Discrepancy is concerned with coloring elements of a ground set such that each set in a certain set system is as balanced as possible, i.e., has approximately the same number of elements of each color. The Beck–Fiala theorem is concerned with the case where each element doesn't appear many times across all sets. The theorem guarantees that if each element appears at most times, then the elements can be colored so that the imbalance is at most . Statement Formally, given a universe : = \ and a collection of subsets : S_1, S_2, \ldots, S_m \subseteq /math> such that for each i \in /math>, : \vert \ \vert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Measure Theory")
