|
Density Matrix Embedding Theory
The density matrix embedding theory (DMET) is a numerical technique to solve strongly correlated electronic structure problems. By mapping the system to a fragment plus its entangled quantum bath, the local electron correlation effects on the fragment can be accurately modeled by a post-Hartree–Fock solver. This method has shown high-quality results in 1D- and 2D- Hubbard models, from Princeton.edu, retrieved on 2015-09-07. and in chemical model systems incorporating the fully interacting electronic Hamiltonian, including long-range interactions. The basis of DMET is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. Atomic and molecular systems Within the Hartree–Fock method of quantum chemistry, the antisymmetric wave function is approximated by a single Slater determinant. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation within the Born–Oppenheimer approximation. Therefore, the Hartree–Fock limit is always above this exact energy. The difference is called the ''correlation energy'', a term coined by Löwdin. The concept of the correlation energy was studied earlier by Wigner. A certain amount of electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
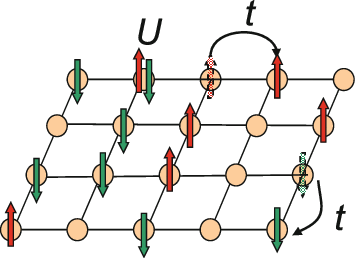
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schmidt Decomposition
In linear algebra, the Schmidt decomposition (named after its originator Erhard Schmidt) refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has numerous applications in quantum information theory, for example in entanglement characterization and in state purification, and plasticity. Theorem Let H_1 and H_2 be Hilbert spaces of dimensions ''n'' and ''m'' respectively. Assume n \geq m. For any vector w in the tensor product H_1 \otimes H_2, there exist orthonormal sets \ \subset H_1 and \ \subset H_2 such that w= \sum_ ^m \alpha _i u_i \otimes v_i, where the scalars \alpha_i are real, non-negative, and unique up to re-ordering. Proof The Schmidt decomposition is essentially a restatement of the singular value decomposition in a different context. Fix orthonormal bases \ \subset H_1 and \ \subset H_2. We can identify an elementary tensor e_i \otimes f_j with the matrix e_i f_j ^\mathsf, where f_j ^\mathsf is the transpos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix used in calculating the probabilities of the outcomes of measurements performed on physical systems. It is a generalization of the state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed states. These arise in quantum mechanics in two different situations: # when the preparation of a system can randomly produce different pure states, and thus one must deal with the statistics of possible preparations, and # when one wants to describe a physical system that is entangled with another, without describing their combined state. This case is typical for a system interacting with some environment (e.g. decoherence). In this case, the density matrix of an entangled system differs from that of an ensemble of pure states that, combined, would give the same statistical results upon measurement. Density matrices are thus crucial tools in areas of quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrices (mathematics)
Matrix (: matrices or matrixes) or MATRIX may refer to: Science and mathematics * Matrix (mathematics), a rectangular array of numbers, symbols or expressions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Technology * Matrix (mass spectrometry), a compound that promotes the formation of ions * Matrix (numismatics), a tool used in coin manufacturing * Matrix (printing), a mould for casting letters * Matrix (protocol), an open standard for real-time communication * Matrix (record production), or master, a disc used in the production of phonograph records ** Matrix number, of a gramophone record * D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Physics
Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline (or offshoot) of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics — an area of study which supplements both theory and experiment. Overview In physics, different theories based on mathematical models provide very precise predictions on how systems behave. Unfortunately, it is often the case that solving the mathematical model for a particular system in order to produce a useful prediction is not feasible. This can occur, for instance, when the solution does not have a closed-form expression, or is too complicated. In such cases, numerical approximations are required. Computational physics is the subject that deals with these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |