|
Degeneracy (math)
In mathematics, a degenerate case is a limiting case of a class of objects which appears to be qualitatively different from (and usually simpler than) the rest of the class, and the term degeneracy is the condition of being a degenerate case. The definitions of many classes of composite or structured objects often implicitly include inequalities. For example, the angles and the side lengths of a triangle are supposed to be positive. The limiting cases, where one or several of these inequalities become equalities, are degeneracies. In the case of triangles, one has a ''degenerate triangle'' if at least one side length or angle is zero. Equivalently, it becomes a "line segment". Often, the degenerate cases are the exceptional cases where changes to the usual dimension or the cardinality of the object (or of some part of it) occur. For example, a triangle is an object of dimension two, and a degenerate triangle is contained in a line, which makes its dimension one. This is simil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
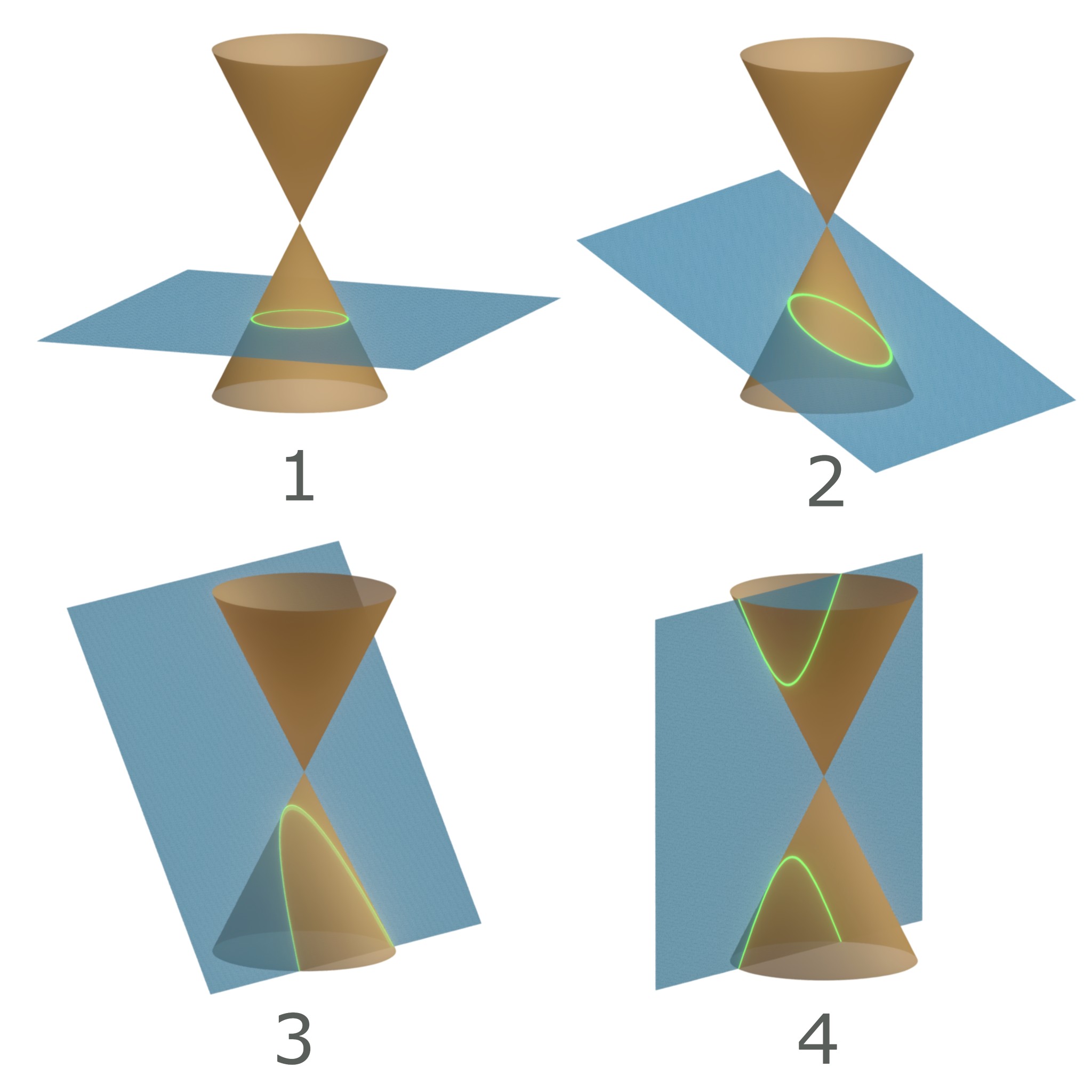
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (), singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of distances to the two foci. A parabola is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiminor Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using a line above the symbols for the two endpoints (such as \overline). Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. When the end points both lie on a curve (such as a circle), a line segment is called a chord (geometry), chord (of that curve). In real or complex vector spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel (geometry)
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have analogous properties that are referred to as parallelism. Symbol The parallel symbol is \parallel. For example, AB \parallel CD indicates that line ''AB'' is parallel to line ''CD''. In the Unicode character set, the "parallel" and "not parallel" signs have codepoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversive Geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotions from any exterior source. An inversive heat source would be a heat source where all the heat remains within the object and is not subject to any format of transference Transference (german: Übertragung) is a phenomenon within psychotherapy in which the "feelings, attitudes, or desires" a person had about one thing are subconsciously projected onto the here-and-now Other. It usually concerns feelings from a ... or externalisation. Is the opposite of Transversive activities and objects which suggest by their very nature that the outcome is transferred to the secondary source. Psychoanalytic terminology Emotion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Plane
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. Similarly, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point where the parabola intersects its axis of symmetry is called the "vertex" and is the point where the parabola is most sharply curved. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In classical Euclidean geometry, a point is a primitive notion that models an exact location in space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space. Being a primitive notion means that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy; for example, ''"there is exactly one line that passes through two different points"''. Points in Euclidean geometry Points, considered within the framework of Euclidean geometry, are one of the most fundamental objects. Euclid originally defined the point as "that which has no part". In two-dimensional Euclidean space, a point is represented by an ordered pair (, ) of numbers, where the first number conventionally represents the horizontal and is often denoted by , and the second number conventionally represents the vertical and is often denoted by . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.png)