|
Dedekind-complete
In mathematics, the least-upper-bound property (sometimes called completeness or supremum property or l.u.b. property) is a fundamental property of the real numbers. More generally, a partially ordered set has the least-upper-bound property if every non-empty subset of with an upper bound has a ''least'' upper bound (supremum) in . Not every (partially) ordered set has the least upper bound property. For example, the set \mathbb of all rational numbers with its natural order does ''not'' have the least upper bound property. The least-upper-bound property is one form of the completeness axiom for the real numbers, and is sometimes referred to as Dedekind completeness.Willard says that an ordered space "X is Dedekind complete if every subset of X having an upper bound has a least upper bound." (pp. 124-5, Problem 17E.) It can be used to prove many of the fundamental results of real analysis, such as the intermediate value theorem, the Bolzano–Weierstrass theorem, the extreme va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limit (mathematics), limits, continuous function, continuity and derivatives. The set of real numbers is mathematical notation, denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers subset, include t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Construction Of The Real Numbers
In mathematics, there are several equivalent ways of defining the real numbers. One of them is that they form a complete ordered field that does not contain any smaller complete ordered field. Such a definition does not prove that such a complete ordered field exists, and the existence proof consists of constructing a mathematical structure that satisfies the definition. The article presents several such constructions. They are equivalent in the sense that, given the result of any two such constructions, there is a unique isomorphism of ordered field between them. This results from the above definition and is independent of particular constructions. These isomorphisms allow identifying the results of the constructions, and, in practice, to forget which construction has been chosen. Axiomatic definitions An axiomatic definition of the real numbers is to define them as the elements of a complete ordered field. Precisely, this means the following. A ''model for the real number syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extreme Value Theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous on the closed interval ,b/math>, then f must attain a maximum and a minimum, each at least once. That is, there exist numbers c and d in ,b/math> such that: f(c) \ge f(x) \ge f(d)\quad \forall x\in ,b/math> The extreme value theorem is more specific than the related boundedness theorem, which states merely that a continuous function f on the closed interval ,b/math> is bounded on that interval; that is, there exist real numbers m and M such that: m \le f(x) \le M\quad \forall x \in , b This does not say that M and m are necessarily the maximum and minimum values of f on the interval ,b which is what the extreme value theorem stipulates must also be the case. The extreme value theorem is used to prove Rolle's theorem. In a formulation due to Karl Weierstrass, this theorem states that a continuous function from a non-empty compact space to a subset of the real numbers attains ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Illustration Of Supremum
An illustration is a decoration, interpretation or visual explanation of a text, concept or process, designed for integration in print and digital published media, such as posters, flyers, magazines, books, teaching materials, animations, video games and films. An illustration is typically created by an illustrator. Digital illustrations are often used to make websites and apps more user-friendly, such as the use of emojis to accompany digital type. llustration also means providing an example; either in writing or in picture form. The origin of the word "illustration" is late Middle English (in the sense ‘illumination; spiritual or intellectual enlightenment’): via Old French from Latin ''illustratio''(n-), from the verb ''illustrare''. Illustration styles Contemporary illustration uses a wide range of styles and techniques, including drawing, painting, printmaking, collage, montage, digital design, multimedia, 3D modelling. Depending on the purpose, illustratio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra under the subset relation, in which the join and meet are given by intersection and union, and the subset relation itself is the Boolean inclusion relation. Definition If ''A'' and ''B'' are sets and every element of ''A'' is also an element of ''B'', then: :*''A'' is a subset of ''B'', denoted by A \subseteq B, or equivalently, :* ''B'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Continuum
In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line. Formally, a linear continuum is a linearly ordered set ''S'' of more than one element that is densely ordered, i.e., between any two distinct elements there is another (and hence infinitely many others), and complete, i.e., which "lacks gaps" in the sense that every nonempty subset with an upper bound has a least upper bound. More symbolically: ''S'' has the least upper bound property, and For each ''x'' in ''S'' and each ''y'' in ''S'' with ''x'' < ''y'', there exists ''z'' in ''S'' such that ''x'' < ''z'' < ''y'' A set has the least upper bound property, if every nonempty subset of the set that is bounded above has a least upper bound in the set. Linear continua are particularly important in the field of |
Supremum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lower bound'' (abbreviated as ) is also commonly used. The supremum (abbreviated sup; plural suprema) of a subset S of a partially ordered set P is the least element in P that is greater than or equal to each element of S, if such an element exists. Consequently, the supremum is also referred to as the ''least upper bound'' (or ). The infimum is in a precise sense dual to the concept of a supremum. Infima and suprema of real numbers are common special cases that are important in analysis, and especially in Lebesgue integration. However, the general definitions remain valid in the more abstract setting of order theory where arbitrary partially ordered sets are considered. The concepts of infimum and supremum are close to minimum and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
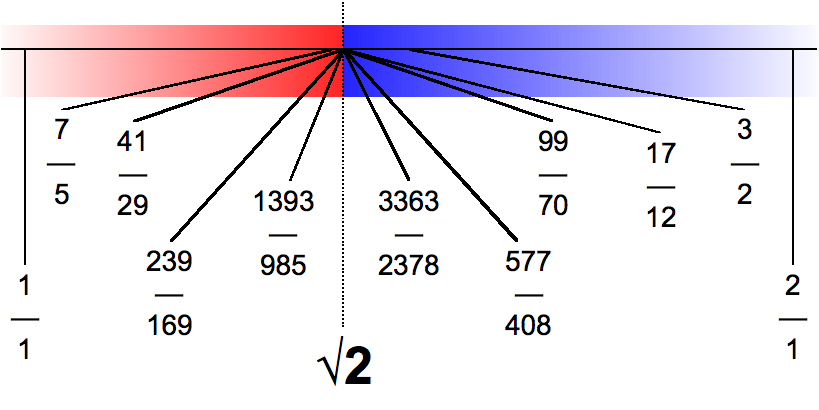
Dedekind Cut- Square Root Of Two
Julius Wilhelm Richard Dedekind (6 October 1831 – 12 February 1916) was a German mathematician who made important contributions to number theory, abstract algebra (particularly ring theory), and the axiomatic foundations of arithmetic. His best known contribution is the definition of real numbers through the notion of Dedekind cut. He is also considered a pioneer in the development of modern set theory and of the philosophy of mathematics known as ''Logicism''. Life Dedekind's father was Julius Levin Ulrich Dedekind, an administrator of Collegium Carolinum in Braunschweig. His mother was Caroline Henriette Dedekind (née Emperius), the daughter of a professor at the Collegium. Richard Dedekind had three older siblings. As an adult, he never used the names Julius Wilhelm. He was born in Braunschweig (often called "Brunswick" in English), which is where he lived most of his life and died. He first attended the Collegium Carolinum in 1848 before transferring to the University ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Completeness Axiom
Completeness is a property of the real numbers that, intuitively, implies that there are no "gaps" (in Dedekind's terminology) or "missing points" in the real number line. This contrasts with the rational numbers, whose corresponding number line has a "gap" at each irrational value. In the decimal number system, completeness is equivalent to the statement that any infinite string of decimal digits is actually a decimal representation for some real number. Depending on the construction of the real numbers used, completeness may take the form of an axiom (the completeness axiom), or may be a theorem proven from the construction. There are many equivalent forms of completeness, the most prominent being Dedekind completeness and Cauchy completeness ( completeness as a metric space). Forms of completeness The real numbers can be defined synthetically as an ordered field satisfying some version of the ''completeness axiom''. Different versions of this axiom are all equivalent in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearly Ordered Set
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor (Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |