|
Castelnuovo's Contraction Theorem
In mathematics, Castelnuovo's contraction theorem is used in the classification theory of algebraic surfaces to construct the minimal model of a given smooth algebraic surface. More precisely, let X be a smooth projective surface over \mathbb and C a (−1)-curve on X (which means a smooth rational curve of self-intersection number −1), then there exists a morphism from X to another smooth projective surface Y such that the curve C has been contracted to one point P, and moreover this morphism is an isomorphism outside C (i.e., X\setminus C is isomorphic with Y\setminus P). This contraction morphism is sometimes called a blowdown, which is the inverse operation of blowup. The curve C is also called an exceptional curve of the first kind. References * *{{Citation , last1=Kollár , first1=János , last2=Mori , first2=Shigefumi , author2-link=Shigefumi Mori , author1-link=János Kollár , title=Birational geometry of algebraic varieties , publisher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
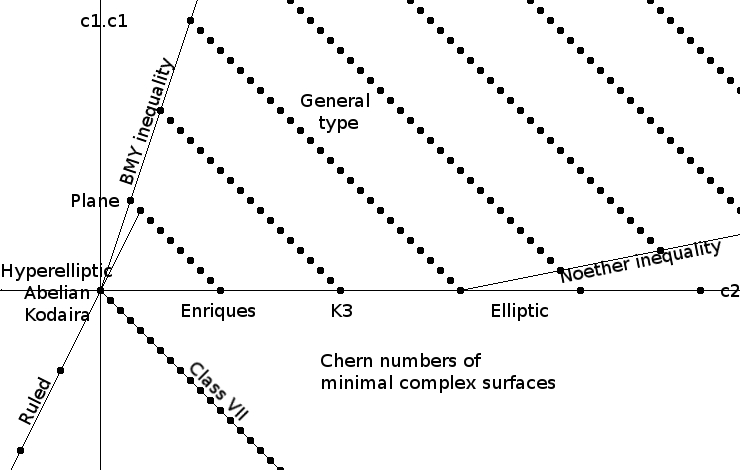
Enriques–Kodaira Classification
In mathematics, the Enriques–Kodaira classification is a classification of compact complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space. For most of the classes the moduli spaces are well understood, but for the class of surfaces of general type the moduli spaces seem too complicated to describe explicitly, though some components are known. Max Noether began the systematic study of algebraic surfaces, and Guido Castelnuovo proved important parts of the classification. described the classification of complex projective surfaces. later extended the classification to include non-algebraic compact surfaces. The analogous classification of surfaces in positive characteristic was begun by and completed by ; it is similar to the characteristic 0 projective case, except that one also gets singular and supersingular Enriques surfaces in characteristic 2, and quasi-hyperelliptic surfaces in characteristics 2 and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two (as a complex manifold, when it is non-singular) and so of dimension four as a smooth manifold. The theory of algebraic surfaces is much more complicated than that of algebraic curves (including the compact Riemann surfaces, which are genuine surfaces of (real) dimension two). Many results were obtained, however, in the Italian school of algebraic geometry, and are up to 100 years old. Classification by the Kodaira dimension In the case of dimension one varieties are classified by only the topological genus, but dimension two, the difference between the arithmetic genus p_a and the geometric genus p_g turns to be important because we cannot distinguish birationally only the topological genus. Then we introduce the irregularity for the classification of them. A summary of the results (in det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Model Program
In algebraic geometry, the minimal model program is part of the birational classification of algebraic varieties. Its goal is to construct a birational model of any complex projective variety which is as simple as possible. The subject has its origins in the classical birational geometry of surfaces studied by the Italian school, and is currently an active research area within algebraic geometry. Outline The basic idea of the theory is to simplify the birational classification of varieties by finding, in each birational equivalence class, a variety which is "as simple as possible". The precise meaning of this phrase has evolved with the development of the subject; originally for surfaces, it meant finding a smooth variety X for which any birational morphism f\colon X \to X' with a smooth surface X' is an isomorphism. In the modern formulation, the goal of the theory is as follows. Suppose we are given a projective variety X, which for simplicity is assumed non-singular. There are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Variety
In algebraic geometry, a smooth scheme over a field is a scheme which is well approximated by affine space near any point. Smoothness is one way of making precise the notion of a scheme with no singular points. A special case is the notion of a smooth variety over a field. Smooth schemes play the role in algebraic geometry of manifolds in topology. Definition First, let ''X'' be an affine scheme of finite type over a field ''k''. Equivalently, ''X'' has a closed immersion into affine space ''An'' over ''k'' for some natural number ''n''. Then ''X'' is the closed subscheme defined by some equations ''g''1 = 0, ..., ''g''''r'' = 0, where each ''gi'' is in the polynomial ring ''k'' 'x''1,..., ''x''''n'' The affine scheme ''X'' is smooth of dimension ''m'' over ''k'' if ''X'' has dimension at least ''m'' in a neighborhood of each point, and the matrix of derivatives (∂''g''''i''/∂''x''''j'') has rank at least ''n''−''m'' everywhere on ''X''. (It follows that ''X'' has dimension ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection Theory
In mathematics, intersection theory is one of the main branches of algebraic geometry, where it gives information about the intersection of two subvarieties of a given variety. The theory for varieties is older, with roots in Bézout's theorem on curves and elimination theory. On the other hand, the topological theory more quickly reached a definitive form. There is yet an ongoing development of intersection theory. Currently the main focus is on: virtual fundamental cycles, quantum intersection rings, Gromov-Witten theory and the extension of intersection theory from schemes to stacks. Topological intersection form For a connected oriented manifold of dimension the intersection form is defined on the -th cohomology group (what is usually called the 'middle dimension') by the evaluation of the cup product on the fundamental class in . Stated precisely, there is a bilinear form :\lambda_M \colon H^n(M,\partial M) \times H^n(M,\partial M)\to \mathbf given by :\lambda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morphism Of Varieties
In algebraic geometry, a morphism between algebraic varieties is a function between the varieties that is given locally by polynomials. It is also called a regular map. A morphism from an algebraic variety to the affine line is also called a regular function. A regular map whose inverse is also regular is called biregular, and they are isomorphisms in the category of algebraic varieties. Because regular and biregular are very restrictive conditions – there are no non-constant regular functions on projective varieties – the weaker condition of a rational map and birational maps are frequently used as well. Definition If ''X'' and ''Y'' are closed subvarieties of \mathbb^n and \mathbb^m (so they are affine varieties), then a regular map f\colon X\to Y is the restriction of a polynomial map \mathbb^n\to \mathbb^m. Explicitly, it has the form: :f = (f_1, \dots, f_m) where the f_is are in the coordinate ring of ''X'': :k = k _1, \dots, x_nI, where ''I'' is the ideal defining ''X'' ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contraction Morphism
In algebraic geometry, a contraction morphism is a surjective projective morphism f: X \to Y between normal projective varieties (or projective schemes) such that f_* \mathcal_X = \mathcal_Y or, equivalently, the geometric fibers are all connected ( Zariski's connectedness theorem). It is also commonly called an algebraic fiber space, as it is an analog of a fiber space in algebraic topology. By the Stein factorization, any surjective projective morphism is a contraction morphism followed by a finite morphism. Examples include ruled surfaces and Mori fiber spaces. Birational perspective The following perspective is crucial in birational geometry (in particular in Mori's minimal model program). Let ''X'' be a projective variety and \overline(X) the closure of the span of irreducible curves on ''X'' in N_1(X) = the real vector space of numerical equivalence classes of real 1-cycles on ''X''. Given a face ''F'' of \overline(X), the contraction morphism associated to ''F'', if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blowing Down
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion. Blowups are the most fundamental transformation in birational geometry, because every birational morphism between projective varieties is a blowup. The weak factorization theorem says that every birational map can be factored as a composition of particularly simple blowups. The Cremona group, the group of birational automorphisms of the plane, is generated by blowups. Besides their importance in describing birational transformations, blowups are also an important way of constructing new spaces. For instance, most procedures for resolution of singularities proceed by blowin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blowing Up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion. Blowups are the most fundamental transformation in birational geometry, because every birational morphism between projective varieties is a blowup. The weak factorization theorem says that every birational map can be factored as a composition of particularly simple blowups. The Cremona group, the group of birational automorphisms of the plane, is generated by blowups. Besides their importance in describing birational transformations, blowups are also an important way of constructing new spaces. For instance, most procedures for resolution of singularities proceed by bl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exceptional Curve
In mathematics, specifically algebraic geometry, an exceptional divisor for a regular map :f: X \rightarrow Y of varieties is a kind of 'large' subvariety of X which is 'crushed' by f, in a certain definite sense. More strictly, ''f'' has an associated exceptional locus which describes how it identifies nearby points in codimension one, and the exceptional divisor is an appropriate algebraic construction whose support is the exceptional locus. The same ideas can be found in the theory of holomorphic mappings of complex manifolds. More precisely, suppose that :f: X \rightarrow Y is a regular map of varieties which is birational (that is, it is an isomorphism between open subsets of X and Y). A codimension-1 subvariety Z \subset X is said to be ''exceptional'' if f(Z) has codimension at least 2 as a subvariety of Y. One may then define the ''exceptional divisor'' of f to be :\sum_i Z_i \in Div(X), where the sum is over all exceptional subvarieties of f, and is an element of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |