|
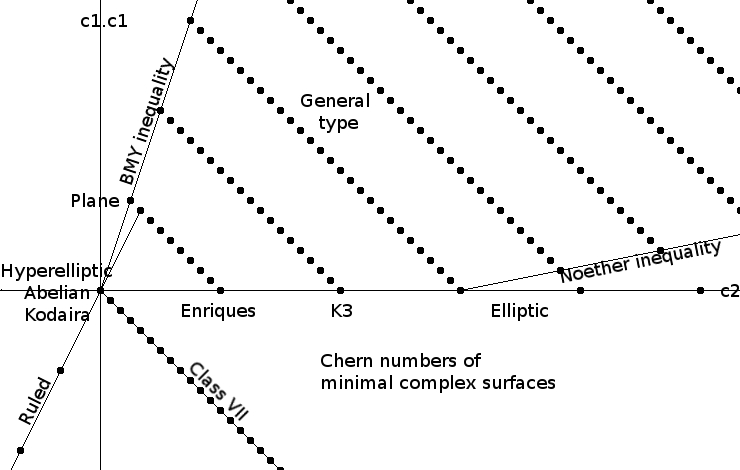
Enriques–Kodaira Classification
In mathematics, the Enriques–Kodaira classification is a classification of compact complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space. For most of the classes the moduli spaces are well understood, but for the class of surfaces of general type the moduli spaces seem too complicated to describe explicitly, though some components are known. Max Noether began the systematic study of algebraic surfaces, and Guido Castelnuovo proved important parts of the classification. described the classification of complex projective surfaces. later extended the classification to include non-algebraic compact surfaces. The analogous classification of surfaces in positive characteristic was begun by and completed by ; it is similar to the characteristic 0 projective case, except that one also gets singular and supersingular Enriques surfaces in characteristic 2, and quasi-hyperelliptic surfaces in characteristics 2 and 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plurigenera
In mathematics, the pluricanonical ring of an algebraic variety ''V'' (which is non-singular), or of a complex manifold, is the graded ring :R(V,K)=R(V,K_V) \, of sections of powers of the canonical bundle ''K''. Its ''n''th graded component (for n\geq 0) is: :R_n := H^0(V, K^n),\ that is, the space of sections of the ''n''-th tensor product ''K''''n'' of the canonical bundle ''K''. The 0th graded component R_0 is sections of the trivial bundle, and is one-dimensional as ''V'' is projective. The projective variety defined by this graded ring is called the canonical model of ''V'', and the dimension of the canonical model is called the Kodaira dimension of ''V''. One can define an analogous ring for any line bundle ''L'' over ''V''; the analogous dimension is called the Iitaka dimension. A line bundle is called big if the Iitaka dimension equals the dimension of the variety. Properties Birational invariance The canonical ring and therefore likewise the Kodaira dimension is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by \chi ( Greek lower-case letter chi). The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico. Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra. Polyhedra The Euler characteristic \chi was classically defined for the surfaces of polyhedra, acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-adic Cohomology
In mathematics, the -adic number system for any prime number extends the ordinary arithmetic of the rational numbers in a different way from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of "closeness" or absolute value. In particular, two -adic numbers are considered to be close when their difference is divisible by a high power of : the higher the power, the closer they are. This property enables -adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory – including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles. These numbers were first described by Kurt Hensel in 1897, though, with hindsight, some of Ernst Kummer's earlier work can be interpreted as implicitly using -adic numbers.Translator's introductionpage 35 "Indeed, with hindsight it becomes apparent that a di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betti Number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicial complexes or CW complexes), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite. The ''n''th Betti number represents the rank of the ''n''th homology group, denoted ''H''''n'', which tells us the maximum number of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc. For example, if H_n(X) \cong 0 then b_n(X) = 0, if H_n(X) \cong \mathbb then b_n(X) = 1, if H_n(X) \cong \mathbb \oplus \mathbb then b_n(X) = 2, if H_n(X) \cong \mathbb \oplus \mathbb\oplus \mathbb then b_n(X) = 3, etc. Note that only the ranks of infinite groups are considered, so for example if H_n(X) \cong \mathbb^k \oplus \mathbb/(2) , where \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory. From its beginning in topology, this idea became a dominant method in the mathematics of the second half of the twentieth century. From the initial idea of homology as a method of constructing algebraic invariants of topological spaces, the range of applications of homology and cohomology theories has spread throughout geometry and algebra. The terminology tends to hide the fact that cohomology, a contravariant theory, is more natural than homology in many applications. At a basic level, this has to d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Serre Duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality for the coherent sheaf cohomology of algebraic varieties, proved by Jean-Pierre Serre. The basic version applies to vector bundles on a smooth projective variety, but Alexander Grothendieck found wide generalizations, for example to singular varieties. On an ''n''-dimensional variety, the theorem says that a cohomology group H^i is the dual space of another one, H^. Serre duality is the analog for coherent sheaf cohomology of Poincaré duality in topology, with the canonical line bundle replacing the orientation sheaf. The Serre duality theorem is also true in complex geometry more generally, for compact complex manifolds that are not necessarily projective complex algebraic varieties. In this setting, the Serre duality theorem is an application of Hodge theory for Dolbeault cohomology, and may be seen as a result in the theory of elliptic operators. These two different interpretations of Serre dual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hodge Number
In mathematics, Hodge theory, named after W. V. D. Hodge, is a method for studying the cohomology groups of a smooth manifold ''M'' using partial differential equations. The key observation is that, given a Riemannian metric on ''M'', every cohomology class has a canonical representative, a differential form that vanishes under the Laplacian operator of the metric. Such forms are called harmonic. The theory was developed by Hodge in the 1930s to study algebraic geometry, and it built on the work of Georges de Rham on de Rham cohomology. It has major applications in two settings: Riemannian manifolds and Kähler manifolds. Hodge's primary motivation, the study of complex projective varieties, is encompassed by the latter case. Hodge theory has become an important tool in algebraic geometry, particularly through its connection to the study of algebraic cycles. While Hodge theory is intrinsically dependent upon the real and complex numbers, it can be applied to questions in numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (''analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term ''analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to as '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kodaira Dimension
In algebraic geometry, the Kodaira dimension ''κ''(''X'') measures the size of the canonical model of a projective variety ''X''. Igor Shafarevich, in a seminar introduced an important numerical invariant of surfaces with the notation ''κ''. Shigeru Iitaka extended it and defined the Kodaira dimension for higher dimensional varieties (under the name of canonical dimension), and later named it after Kunihiko Kodaira. The plurigenera The canonical bundle of a smooth algebraic variety ''X'' of dimension ''n'' over a field is the line bundle of ''n''-forms, :\,\!K_X = \bigwedge^n\Omega^1_X, which is the ''n''th exterior power of the cotangent bundle of ''X''. For an integer ''d'', the ''d''th tensor power of ''K''''X'' is again a line bundle. For ''d'' ≥ 0, the vector space of global sections ''H''0(''X'',''K''''X''''d'') has the remarkable property that it is a birational invariant of smooth projective varieties ''X''. That is, this vector space is canonically ident ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kähler Manifold
In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil. Kähler geometry refers to the study of Kähler manifolds, their geometry and topology, as well as the study of structures and constructions that can be performed on Kähler manifolds, such as the existence of special connections like Hermitian Yang–Mills connections, or special metrics such as Kähler–Einstein metrics. Every smooth complex projective variety is a Kähler manifold. Hodge theory is a central part of algebraic geometry, proved using Kähler metrics. Definitions Since Kähler manifolds are equipped with several compatible structures, they can be described from different points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Morgan (mathematician)
John Willard Morgan (born March 21, 1946) is an American mathematician known for his contributions to topology and geometry. He is a Professor Emeritus at Columbia University and a member of the Simons Center for Geometry and Physics at Stony Brook University. Life Morgan received his B.A. in 1968 and Ph.D. in 1969, both from Rice University. His Ph.D. thesis, entitled ''Stable tangential homotopy equivalences'', was written under the supervision of Morton L. Curtis. He was an instructor at Princeton University from 1969 to 1972, and an assistant professor at MIT from 1972 to 1974. He has been on the faculty at Columbia University since 1974, serving as the Chair of the Department of Mathematics from 1989 to 1991 and becoming Professor Emeritus in 2010. Morgan is a member of the Simons Center for Geometry and Physics at Stony Brook University and served as its founding director from 2009 to 2016. From 1974 to 1976, Morgan was a Sloan Research Fellow. In 2008, he was aw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |