|
CP2K
CP2K is a freely available ( GPL) quantum chemistry and solid state physics program package, written in Fortran 2008, to perform atomistic simulations of solid state, liquid, molecular, periodic, material, crystal, and biological systems. It provides a general framework for different methods: density functional theory (DFT) using a mixed Gaussian and plane waves approach (GPW) via LDA, GGA, MP2, or RPA levels of theory, classical pair and many-body potentials, semi-empirical ( AM1, PM3, MNDO, MNDOd, PM6) and tight-binding Hamiltonians, as well as Quantum Mechanics/Molecular Mechanics (QM/MM) hybrid schemes relying on the Gaussian Expansion of the Electrostatic Potential (GEEP). The Gaussian and Augmented Plane Waves method (GAPW) as an extension of the GPW method allows for all-electron calculations. CP2K can do simulations of molecular dynamics, metadynamics, Monte Carlo, Ehrenfest dynamics, vibrational analysis, core level spectroscopy, energy minimization, and transition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Minimization
In the field of computational chemistry, energy minimization (also called energy optimization, geometry minimization, or geometry optimization) is the process of finding an arrangement in space of a collection of atoms where, according to some computational model of chemical bonding, the net inter-atomic force on each atom is acceptably close to zero and the position on the potential energy surface (PES) is a stationary point (described later). The collection of atoms might be a single molecule, an ion, a condensed phase, a transition state or even a collection of any of these. The computational model of chemical bonding might, for example, be quantum mechanics. As an example, when optimizing the geometry of a water molecule, one aims to obtain the hydrogen-oxygen bond lengths and the hydrogen-oxygen-hydrogen bond angle which minimize the forces that would otherwise be pulling atoms together or pushing them apart. The motivation for performing a geometry optimization is the phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry Computer Programs
Quantum chemistry computer programs are used in computational chemistry to implement the methods of quantum chemistry. Most include the Hartree–Fock (HF) and some post-Hartree–Fock methods. They may also include density functional theory (DFT), molecular mechanics or semi-empirical quantum chemistry methods. The programs include both open source Open source is source code that is made freely available for possible modification and redistribution. Products include permission to use the source code, design documents, or content of the product. The open-source model is a decentralized sof ... and commercial software. Most of them are large, often containing several separate programs, and have been developed over many years. Overview The following tables illustrates some of the main capabilities of notable packages: Numerical details Quantum chemistry and solid-state physics characteristics Post processing packages in quantum chemistry and solid-state physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Car–Parrinello Molecular Dynamics
Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics (also known as the Car–Parrinello method) or the computational chemistry software package used to implement this method. The CPMD method is one of the major methods for calculating ab-initio molecular dynamics (ab-inito MD or AIMD). Ab initio molecular dynamics (ab initio MD) is a computational method that uses first principles, or fundamental laws of nature, to simulate the motion of atoms in a system. It is a type of molecular dynamics (MD) simulation that does not rely on empirical potentials or force fields to describe the interactions between atoms, but rather calculates these interactions directly from the electronic structure of the system using quantum mechanics. In an ab initio MD simulation, the total energy of the system is calculated at each time step using density functional theory (DFT) or another method of quantum chemistry. The forces acting on each atom are then det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Austin Model 1
Austin Model 1, or AM1, is a semi-empirical method for the quantum calculation of molecular electronic structure in computational chemistry. It is based on the Neglect of Differential Diatomic Overlap integral approximation. Specifically, it is a generalization of the modified neglect of differential diatomic overlap approximation. Related methods are PM3 and the older MINDO. AM1 was developed by Michael Dewar and co-workers and published in 1985. AM1 is an attempt to improve the MNDO model by reducing the repulsion of atoms at close separation distances. The atomic core-atomic core terms in the MNDO equations were modified through the addition of off-center attractive and repulsive Gaussian functions. The complexity of the parameterization problem increased in AM1 as the number of parameters per atom increased from 7 in MNDO to 13-16 per atom in AM1. The results of AM1 calculations are sometimes used as the starting points for parameterizations of forcefields in molec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Mechanics
Molecular mechanics uses classical mechanics to model molecular systems. The Born–Oppenheimer approximation is assumed valid and the potential energy of all systems is calculated as a function of the nuclear coordinates using force fields. Molecular mechanics can be used to study molecule systems ranging in size and complexity from small to large biological systems or material assemblies with many thousands to millions of atoms. All-atomistic molecular mechanics methods have the following properties: * Each atom is simulated as one particle * Each particle is assigned a radius (typically the van der Waals radius), polarizability, and a constant net charge (generally derived from quantum calculations and/or experiment) * Bonded interactions are treated as ''springs'' with an equilibrium distance equal to the experimental or calculated bond length Variants on this theme are possible. For example, many simulations have historically used a ''united-atom'' representation in whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MNDO
MNDO, or Modified Neglect of Diatomic Overlap is a semi-empirical method for the quantum calculation of molecular electronic structure in computational chemistry. It is based on the Neglect of Diatomic Differential Overlap integral approximation. Similarly, this method replaced the earlier MINDO method. It is part of the MOPAC program and was developed in the group of Michael Dewar. It is also part of the AMPAC, GAMESS (US), PC GAMESS, GAMESS (UK), Gaussian, ORCA and CP2K programs. Later, it was essentially replaced by two new methods, PM3 and AM1, which are similar but have different parameterisation methods. The extension by W. Thiel's group, called MNDO/d, which adds d functions, is widely used for organometallic compounds. It is included in GAMESS (UK). MNDOC, also from W. Thiel's group, explicitly adds correlation effects though second order perturbation theory In mathematics and applied mathematics, perturbation theory comprises methods for finding an appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PM3 (chemistry)
PM3, or Parametric Method 3, is a semi-empirical method for the quantum calculation of molecular electronic structure in computational chemistry. It is based on the Neglect of Differential Diatomic Overlap integral approximation. The PM3 method uses the same formalism and equations as the AM1 method. The only differences are: 1) PM3 uses two Gaussian functions for the core repulsion function, instead of the variable number used by AM1 (which uses between one and four Gaussians per element); 2) the numerical values of the parameters are different. The other differences lie in the philosophy and methodology used during the parameterization: whereas AM1 takes some of the parameter values from spectroscopical measurements, PM3 treats them as optimizable values. The method was developed by J. J. P. Stewart and first published in 1989. It is implemented in the MOPAC program (of which the older versions are public domain), along with the related RM1, AM1, MNDO and MINDO met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-empirical Quantum Chemistry Method
Semi-empirical quantum chemistry methods are based on the Hartree–Fock formalism, but make many approximations and obtain some parameters from empirical data. They are very important in computational chemistry for treating large molecules where the full Hartree–Fock method without the approximations is too expensive. The use of empirical parameters appears to allow some inclusion of electron correlation effects into the methods. Within the framework of Hartree–Fock calculations, some pieces of information (such as two-electron integrals) are sometimes approximated or completely omitted. In order to correct for this loss, semi-empirical methods are parametrized, that is their results are fitted by a set of parameters, normally in such a way as to produce results that best agree with experimental data, but sometimes to agree with ''ab initio'' results. Type of simplifications used Semi-empirical methods follow what are often called empirical methods where the two-electron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harris Functional
In density functional theory (DFT), the Harris energy functional is a non-self-consistent approximation to the Kohn–Sham equations, Kohn–Sham density functional theory. It gives the energy of a combined system as a function of the electronic density, electronic densities of the isolated parts. The energy of the Harris functional varies much less than the energy of the Kohn–Sham functional as the density moves away from the converged density. Background Kohn–Sham equations are the one-electron equations that must be solved in a Self-consistency, self-consistent fashion in order to find the Ground State, ground state Electron density, density of a system of Many-body theory, interacting electrons: : \left( \frac\nabla^2+v_[n]+v_[n] +v_(r)\right)\phi_j(r)=\epsilon_j \phi_j(r). The density, n, is given by that of the Slater determinant formed by the Molecular orbital, spin-orbitals of the occupied states: : n(r)=\sum_ f_j \vert \phi_j (r) \vert ^2, where the coefficients ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
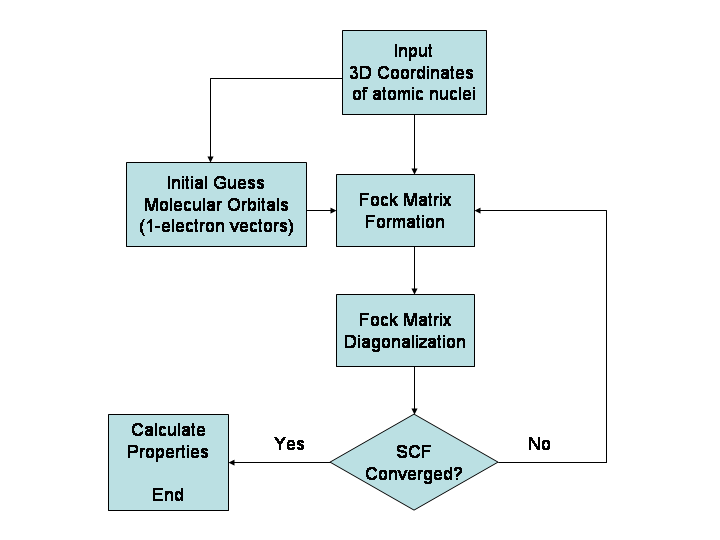
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distributi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of molecules, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the quantization of energy on a molecular scale can be obtained. Common methods are infra-red (IR) spectroscopy, nuclear magnetic r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tight Binding
In solid-state physics, the tight-binding model (or TB model) is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method (linear combination of atomic orbitals method) used in chemistry. Tight-binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight-binding model fails. Though the tight-binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states and application to various kinds of many-body problem and quasiparticle calculations. Introduction The name "tight binding" of this electronic band structure model suggests that this quantum mechanical model describes the properties of tight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |