|
Crossed Modules
In mathematics, and especially in homotopy theory, a crossed module consists of groups G and H, where G acts on H by automorphisms (which we will write on the left, (g,h) \mapsto g \cdot h , and a homomorphism of groups : d\colon H \longrightarrow G, that is equivariant with respect to the conjugation action of G on itself: : d(g \cdot h) = gd(h)g^ and also satisfies the so-called Peiffer identity: : d(h_) \cdot h_ = h_h_h_^ Origin The first mention of the second identity for a crossed module seems to be in footnote 25 on p. 422 of J. H. C. Whitehead's 1941 paper cited below, while the term 'crossed module' is introduced in his 1946 paper cited below. These ideas were well worked up in his 1949 paper 'Combinatorial homotopy II', which also introduced the important idea of a free crossed module. Whitehead's ideas on crossed modules and their applications are developed and explained in the book by Brown, Higgins, Sivera listed below. Some generalisations of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Spaces
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate. A topological space is the most general type of a mathematical space that allows for the definition of limits, continuity, and connectedness. Common types of topological spaces include Euclidean spaces, metric spaces and manifolds. Although very general, the concept of topological spaces is fundamental, and used in virtually every branch of modern mathematics. The study of topological space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CW-complex
A CW complex (also called cellular complex or cell complex) is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead (open access) to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation (often with a much smaller complex). The ''C'' stands for "closure-finite", and the ''W'' for "weak" topology. Definition CW complex A CW complex is constructed by taking the union of a sequence of topological spaces\emptyset = X_ \subset X_0 \subset X_1 \subset \cdotssuch that each X_k is obtained from X_ by gluing copies of k-cells (e^k_\alpha)_\alpha, each homeomorphic to D^k, to X_ by continuous gluing maps g^k_\alpha: \partial e^k_\alpha \to X_. The maps are also called attaching maps. Each X_k is called the k-skeleton of the complex. The topology of X = \cup_ X_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classifying Space
In mathematics, specifically in homotopy theory, a classifying space ''BG'' of a topological group ''G'' is the quotient of a weakly contractible space ''EG'' (i.e. a topological space all of whose homotopy groups are trivial) by a proper free action of ''G''. It has the property that any ''G'' principal bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle ''EG'' → ''BG''. As explained later, this means that classifying spaces represent a set-valued functor on the homotopy category of topological spaces. The term classifying space can also be used for spaces that represent a set-valued functor on the category of topological spaces, such as Sierpiński space. This notion is generalized by the notion of classifying topos. However, the rest of this article discusses the more commonly used notion of classifying space up to homotopy. For a discrete group ''G'', ''BG'' is, roughly speaking, a path-connected topological space ''X'' such that the fundam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2-group
In mathematics, a 2-group, or 2-dimensional higher group, is a certain combination of group and groupoid. The 2-groups are part of a larger hierarchy of ''n''-groups. In some of the literature, 2-groups are also called gr-categories or groupal groupoids. Definition A 2-group is a monoidal category ''G'' in which every morphism is invertible and every object has a weak inverse. (Here, a ''weak inverse'' of an object ''x'' is an object ''y'' such that ''xy'' and ''yx'' are both isomorphic to the unit object.) Strict 2-groups Much of the literature focuses on ''strict 2-groups''. A strict 2-group is a ''strict'' monoidal category in which every morphism is invertible and every object has a strict inverse (so that ''xy'' and ''yx'' are actually equal to the unit object). A strict 2-group is a group object in a category of categories; as such, they are also called ''groupal categories''. Conversely, a strict 2-group is a category object in the category of groups; as such, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Group
{{disambig ...
Categorical may refer to: * Categorical imperative, a concept in philosophy developed by Immanuel Kant * Categorical theory, in mathematical logic * Morley's categoricity theorem, a mathematical theorem in model theory * Categorical data analysis * Categorical distribution, a probability distribution * Categorical logic, a branch of category theory within mathematics with notable connections to theoretical computer science * Categorical syllogism, a kind of logical argument * Categorical proposition, a part of deductive reasoning * Categorization * Categorical perception * Category theory in mathematics ** Categorical set theory * Recursive categorical syntax in linguistics See also *Category (other) Category, plural categories, may refer to: Philosophy and general uses *Categorization, categories in cognitive science, information science and generally *Category of being * ''Categories'' (Aristotle) *Category (Kant) * Categories (Peirce) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality. A category is formed by two sorts of objects: the objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. One often says that a morphism is an ''arrow'' that ''maps'' its source to its target. Morphisms can be ''composed'' if the target of the first morphism equals the source of the second one, and morphism compos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic K-theory
Algebraic ''K''-theory is a subject area in mathematics with connections to geometry, topology, ring theory, and number theory. Geometric, algebraic, and arithmetic objects are assigned objects called ''K''-groups. These are groups in the sense of abstract algebra. They contain detailed information about the original object but are notoriously difficult to compute; for example, an important outstanding problem is to compute the ''K''-groups of the integers. ''K''-theory was discovered in the late 1950s by Alexander Grothendieck in his study of intersection theory on algebraic varieties. In the modern language, Grothendieck defined only ''K''0, the zeroth ''K''-group, but even this single group has plenty of applications, such as the Grothendieck–Riemann–Roch theorem. Intersection theory is still a motivating force in the development of (higher) algebraic ''K''-theory through its links with motivic cohomology and specifically Chow groups. The subject also includes classical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in postnikov-systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation:^ Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Kampen Theorem
A van is a type of road vehicle used for transporting goods or people. Depending on the type of van, it can be bigger or smaller than a pickup truck and SUV, and bigger than a common car. There is some varying in the scope of the word across the different English-speaking countries. The smallest vans, microvans, are used for transporting either goods or people in tiny quantities. Mini MPVs, compact MPVs, and MPVs are all small vans usually used for transporting people in small quantities. Larger vans with passenger seats are used for institutional purposes, such as transporting students. Larger vans with only front seats are often used for business purposes, to carry goods and equipment. Specially-equipped vans are used by television stations as mobile studios. Postal services and courier companies use large step vans to deliver packages. Word origin and usage Van meaning a type of vehicle arose as a contraction of the word caravan. The earliest records of a van as a vehicle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Group
In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent (or the stronger case of homeomorphic) have isomorphic fundamental groups. The fundamental group of a topological space X is denoted by \pi_1(X). Intuition Start with a space (for example, a surface), and some point in it, and all the loops both starting and ending at this point— paths that start at this point, wander around and eventually return to the starting point. Two loops can be combined in an obvious way: travel along the first loop, then along the second. Two loops are considered equivalent if one can be deformed into the other without breakin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
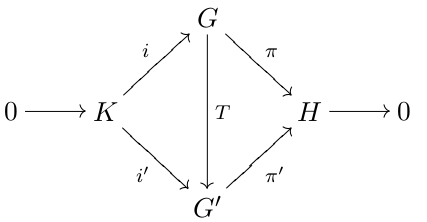
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
