|
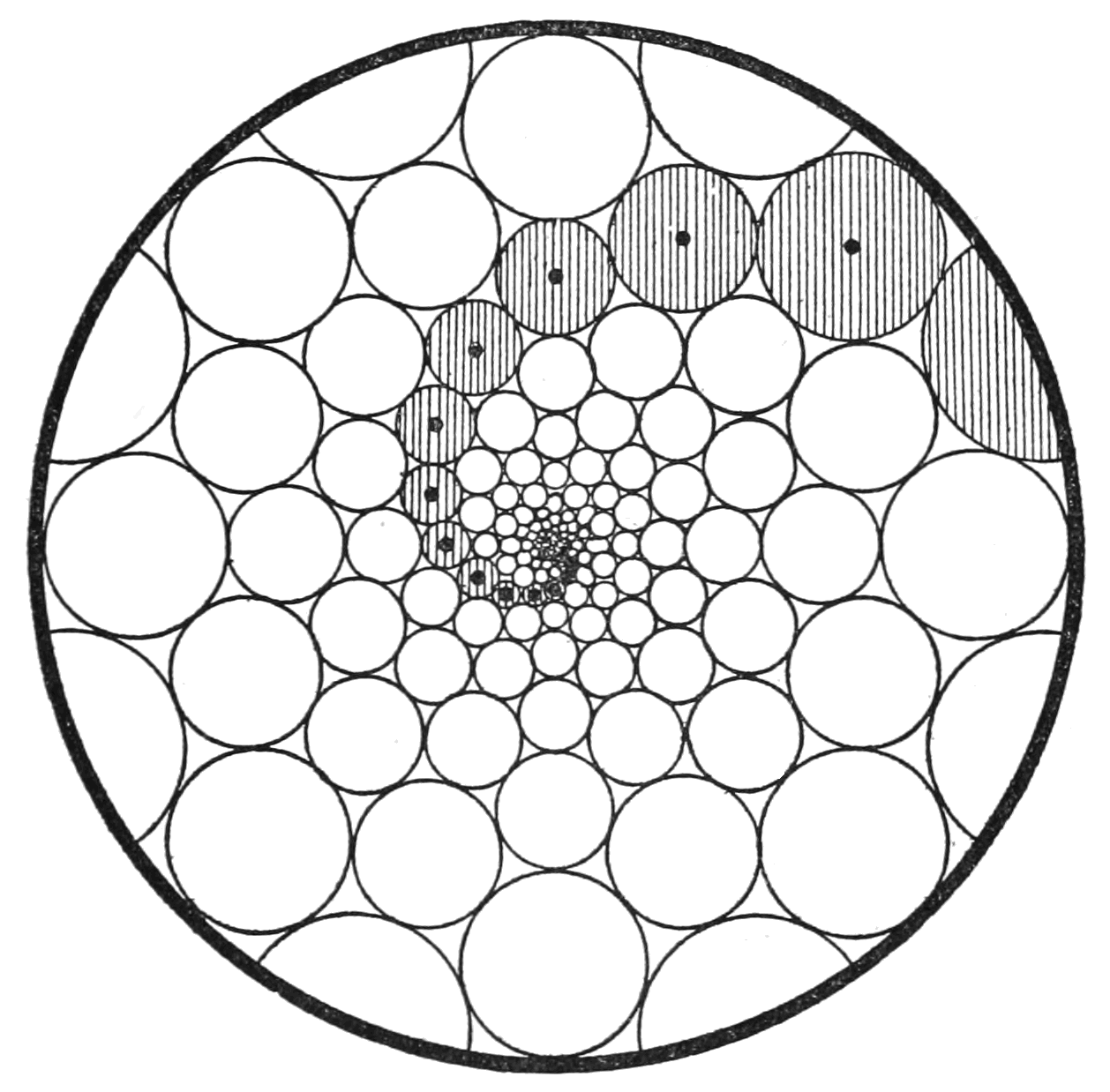
Coxeter's Loxodromic Sequence Of Tangent Circles
In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it. Properties The radii of the circles in the sequence form a geometric progression with ratio k=\varphi + \sqrt \approx 2.89005 \ , where \varphi is the golden ratio. This ratio k and its reciprocal satisfy the equation (1+x+x^2+x^3)^2=2(1+x^2+x^4+x^6)\ , and so any four consecutive circles in the sequence meet the conditions of Descartes' theorem. The centres of the circles in the sequence lie on a logarithmic spiral. Viewed from the centre of the spiral, the angle between the centres of successive circles is \cos^ \left( \frac \right) \approx 128.173 ^ \circ \ . The angle between consecutive triples of centers is \theta=\cos^\frac\approx 51.8273^\circ, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Circles
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the ''common ratio''. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2. Examples of a geometric sequence are powers ''r''''k'' of a fixed non-zero number ''r'', such as 2''k'' and 3''k''. The general form of a geometric sequence is :a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots where ''r'' ≠ 0 is the common ratio and ''a'' ≠ 0 is a scale factor, equal to the sequence's start value. The sum of a geometric progression terms is called a ''geometric series''. Elementary properties The ''n''-th term of a geometric sequence with initial value ''a'' = ''a''1 and common ratio ''r'' is given by :a_n = a\,r^, and in general :a_n = a_m\,r^. Such a geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descartes' Theorem
In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643. History Geometrical problems involving tangent circles have been pondered for millennia. In ancient Greece of the third century BC, Apollonius of Perga devoted an entire book to the topic, ''De tactionibus'' 'On tangencies'' It has been lost, and is known only through mentions of it in other works. René Descartes discussed the problem briefly in 1643, in a letter to Princess Elisabeth of the Palatinate. He came up with the equation describing the relation between the radii, or curvatures, of four pairwise tangent circles. This result became known as Descartes' theorem. This result was rediscovered in 1826 by Jakob Steiner, in 1842 by Philip Beec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewige Linie"). More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it ''Spira mirabilis'', "the marvelous spiral". The logarithmic spiral can be distinguished from the Archimedean spiral by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression, while in an Archimedean spiral these distances are constant. Definition In polar coordinates (r, \varphi) the logarithmic spiral can be written as r = ae^,\quad \varphi \in \R, or \varphi = \frac \ln \frac, with e being the base of natural logarithms, and a > 0, k\ne 0 being real constants. In Cartesian coordinates The logarithmic spiral with the polar equation r = a e^ c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Triangle
A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression is \sqrt\varphi where \varphi=(1+\sqrt)/2 is the golden ratio, and the progression can be written: or approximately . Squares on the edges of this triangle have areas in another geometric progression, 1:\varphi:\varphi^2. Alternative definitions of the same triangle characterize it in terms of the three Pythagorean means of two numbers, or via the inradius of isosceles triangles. This triangle is named after Johannes Kepler, but can be found in earlier sources. Although some sources claim that ancient Egyptian pyramids had proportions based on a Kepler triangle, most scholars believe that the golden ratio was not known to Egyptian mathematics and architecture. History The Kepler triangle is named after the German mathematician and astronomer Johannes Kepler (1571–1630), who wrote about this shape in a 1597 letter. Two concepts that can be used to analyze t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypersphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, called the ''center''. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit -sphere or simply the -sphere for brevity. In terms of the standard norm, the -sphere is defined as : S^n = \left\ , and an -sphere of radius can be defined as : S^n(r) = \left\ . The dimension of -sphere is , and must not be confused with the dimension of the Euclidean space in which it is naturally embedded. An -sphere is the surface or boundary of an -dimensional ball. In particular: *the pair of points at the ends of a (one-dimensional) line segment is a 0-sphere, *a circle, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Doyle Spiral
In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes. Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early Definition A Doyle spiral is defined to be a certain type of circle packing, consisting of infinitely many circles in the plane, with no two circles having overlapping interiors. In a Doyle spiral, each circle is enclosed by a ring of six other circles. The six surrounding circles are tangent to the central circle and to their two neighbors in the Properties Radii As Doyle the only way to pack circl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonian Gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga. Construction The construction of the Apollonian gasket starts with three circles C_1, C_2, and C_3 (black in the figure), that are each tangent to the other two, but that do not have a single point of triple tangency. These circles may be of different sizes to each other, and it is allowed for two to be inside the third, or for all three to be outside each other. As Apollonius discovered, there exist two more circles C_4 and C_5 (red) that are tangent to all three of the original circles – these are called ''Apollonian circles''. These five circles are separated from each other by six curved triangular regions, each bounded by the arcs from three pairwise-tangent circles. The construction continues ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aequationes Mathematicae
''Aequationes Mathematicae'' is a mathematical journal. It is primarily devoted to functional equations, but also publishes papers in dynamical systems, combinatorics, and geometry. As well as publishing regular journal submissions on these topics, it also regularly reports on international symposia on functional equations and produces bibliographies on the subject. János Aczél founded the journal in 1968 at the University of Waterloo, in part because of the long publication delays of up to four years in other journals at the time of its founding. It is currently published by Springer Science+Business Media, with Zsolt Páles of the University of Debrecen as its editor in chief. János Aczél remains its honorary editor in chief. it was listed as a second-quartile mathematics journal by SCImago Journal Rank The SCImago Journal Rank (SJR) indicator is a measure of the prestige of scholarly journals that accounts for both the number of citations received by a journal and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |