Doyle Spiral

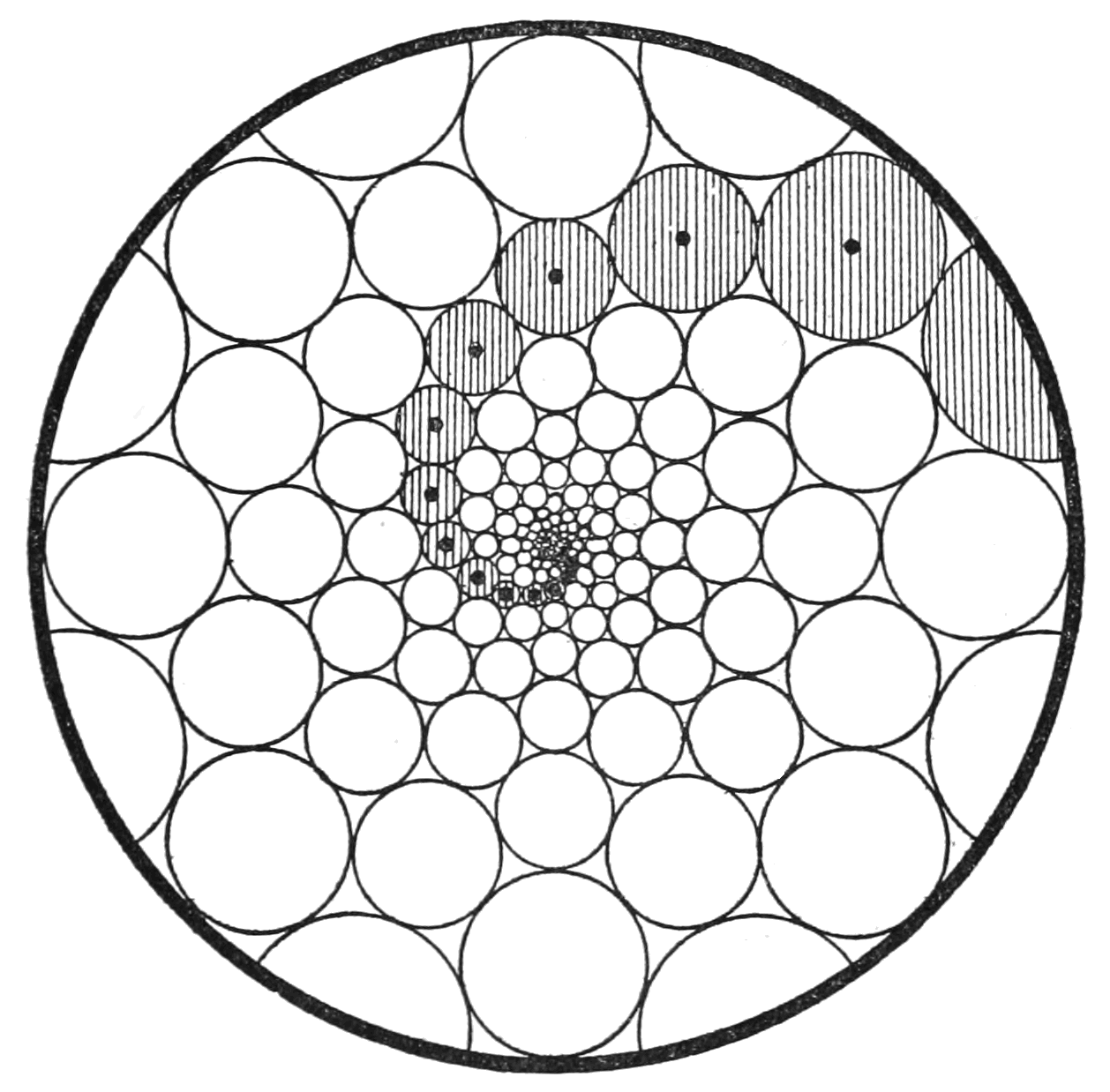
In the mathematics of circle packing, a Doyle spiral is a pattern of non-crossing circles in the plane in which each circle is surrounded by a ring of six tangent circles. These patterns contain spiral arms formed by circles linked through opposite points of tangency, with their centers on logarithmic spirals of three different shapes.

Doyle spirals are named after mathematician Peter G. Doyle, who made an important contribution to their mathematical construction in the late 1980s or However, their study in phyllotaxis (the mathematics of plant growth) dates back to the early

Definition

A Doyle spiral is defined to be a certain type of circle packing, consisting of infinitely many circles in the plane, with no two circles having overlapping interiors. In a Doyle spiral, each circle is enclosed by a ring of six other circles. The six surrounding circles are tangent to the central circle and to their two neighbors in the

Properties

Radii

As Doyle the only way to pack circles with the combinatorial structure of a Doyle spiral is to use circles whose radii are also highly For any such packing, there must exist three positive real numbers so that each circle of radius $r$ is surrounded by circles whose radii are (in cyclic order)

Only certain triples of numbers come from Doyle spirals; others correspond to systems of circles that eventually overlap each

Arms

In a Doyle spiral, one can group the circles into connecting chains of circles through opposite points of tangency. These have been called ''arms'', following the same terminology used for Within each arm, the circles have radii in a doubly infinite geometric sequence
$\dots, ra^, ra^, r, ra, ra^2, \dots$
or a sequence of the same type with common multiplier $b$ In most Doyle spirals, the centers of the circles on a single arm lie on a logarithmic spiral, and all of the logarithmic spirals obtained in this way meet at a single central point. Some Doyle spirals instead have concentric circular arms (as in the stained glass window shown) or straight

Counting the arms

The precise shape of any Doyle spiral can be parameterized by three natural numbers, counting the number of arms of each of its three shapes. When one shape of arm occurs infinitely often, its count is defined as 0, rather The smallest arm count equals the difference of the other two arm counts, so any Doyle spiral can be described as being of where $p$ and $q$ are the two largest counts, in the sorted order

Every pair $(p,q)$ with 1 determines a Doyle spiral, with its third and smallest arm count equal to $q-p$. The shape of this spiral is determined uniquely by these counts, up to For a spiral of the radius multipliers are algebraic numbers whose polynomials can be determined from $p$ These radius multipliers can be accurately approximated by a numerical search, and the results of this search can be used to determine numerical values for the sizes and positions of all of the

Symmetry

Doyle spirals have symmetries that combine scaling and rotation around the central point (or translation and rotation, in the case of the regular hexagonal packing of the plane by unit circles), taking any circle of the packing to any other circle. Applying a Möbius transformation to a Doyle spiral preserves the shape and tangencies of its circles. Therefore, a Möbius transformation can produce additional patterns of non-crossing tangent circles, each tangent to six others. These patterns typically have a double-spiral pattern in which the connected sequences of circles spiral out of one center point (the image of the center of the Doyle spiral) and into another point (the image of the point at infinity). However, these do not meet all of the requirements of Doyle spirals: some circles in this pattern will not be surrounded by their six neighboring

Examples and special cases

The most general case of a Doyle spiral has three distinct radius multipliers, all different and three distinct arm counts, all nonzero. An example is Coxeter's loxodromic sequence of tangent circles, a Doyle spiral of type (2,3), with arm counts 1, 2, and 3, and with radius multipliers and where $\varphi$ denotes the golden ratio. Within the single spiral arm of tightest curvature, the circles in Coxeter's loxodromic sequence form a sequence whose radii are powers of $a$. Every four consecutive circles in this sequence are

When exactly one of the three arm counts is zero, the arms that it counts are circular, with radius The number of circles in each of these circular arms equals the number of arms of each of the other two types. All the circular arms are concentric, centered where the spiral arms In the photo of a stained glass church window, the two rings of nine circles belong to a Doyle spiral of this form, of

Straight arms are produced for arm counts In this case, the two spiraling arm types have the same radius multiplier, and are mirror reflections of each other. There are twice as many straight arms as there are spirals of either type. Each straight arm is formed by circles with centers that lie on a ray through the central Because the number of straight arms must be even, the straight arms can be grouped into opposite pairs, with the two rays from each pair meeting to form a line. The Doyle spiral of type (8,16) from the ''Popular Science'' illustration is an example, with eight arms spiraling the same way as the shaded arm, another eight reflected arms, and sixteen rays.

A final special case is the Doyle spiral of type (0,0), a regular hexagonal packing of the plane by unit circles. Its radius multipliers are all one and its arms form parallel families of lines of three different

Applications

The Doyle spirals form a discrete analogue of the exponential function, as part of the more general use of circle packings as discrete analogues of conformal maps. Indeed, patterns closely resembling Doyle spirals (but made of tangent shapes that are not circles) can be obtained by applying the exponential map to a scaled copy of the regular hexagonal circle The three ratios of radii between adjacent circles, fixed throughout the spiral, can be seen as analogous to a characterization of the exponential map as having fixed Doyle spirals have been used to study Kleinian groups, discrete groups of symmetries of hyperbolic space, by embedding these spirals onto the sphere at infinity of hyperbolic space and lifting the symmetries of each spiral to symmetries of the space

Spirals of tangent circles, often with Fibonacci numbers of arms, have been used to model phyllotaxis, the spiral growth patterns characteristic of certain plant species, beginning with the work of Gerrit van Iterson In this context, an arm of the Doyle spiral is called a parastichy and the arm counts of the Doyle spiral are called ''parastichy numbers''. When the two parastichy numbers $p$ and $q$ are Fibonacci numbers, and either consecutive or separated by only one Fibonacci number, then the third parastichy number will also be a Fibonacci With this application in mind, Arnold Emch in 1910 calculated the positions of circles in Doyle spirals of noting in his work the connections between these spirals, logarithmic spirals, and the exponential For modeling plant growth in this way, spiral packings of tangent circles on surfaces other than the plane, including cylinders and cones, may also be

Spiral packings of circles have also been studied as a decorative motif in

Related patterns

Tangent circles can form spiral patterns whose local structure resembles a square grid rather than a hexagonal grid, which can be continuously transformed into Doyle The space of locally-square spiral packings is infinite-dimensional, unlike Doyle spirals, which can be determined by a constant number of parameters. It is also possible to describe spiraling systems of overlapping circles that cover the plane, rather than non-crossing circles that pack the plane, with each point of the plane covered by at most two circles except for points where three circles meet at $60^\circ$ angles, and with each circle surrounded by six others. These have many properties in common with the Doyle

The Doyle spiral should not be confused with a different spiral pattern of circles, studied for certain forms of plant growth such as the seed heads of sunflowers. In this pattern, the circles are of unit size rather than growing logarithmically, and are not tangent. Instead of having centers on a logarithmic spiral, they are placed on Fermat's spiral, offset by the golden angle $2\pi/\varphi^2\approx 137.5^\circ$ from each other relative to the center of the spiral, where $\varphi$ is the

References

Further reading

*

External links

Doyle spiral explorer
Robin Houston

{{Spirals
Circle packing
Spirals
Plant morphology