|
Configural Frequency Analysis
Configural frequency analysis (CFA) is a method of exploratory data analysis, introduced by Gustav A. Lienert in 1969. The goal of a configural frequency analysis is to detect patterns in the data that occur significantly more (such patterns are called ''Types'') or significantly less often (such patterns are called ''Antitypes'') than expected by chance. Thus, the idea of a CFA is to provide by the identified types and antitypes some insight into the structure of the data. Types are interpreted as concepts which are constituted by a pattern of variable values. Antitypes are interpreted as patterns of variable values that do in general not occur together. Basic idea of the CFA algorithm We explain the basic idea of CFA by a simple example. Assume that we have a data set that describes for each of ''n'' patients if they show certain symptoms ''s''1, ..., ''s''''m''. We assume for simplicity that a symptom is shown or not, i.e. we have a dichotomous data set. Each record in the da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exploratory Data Analysis
In statistics, exploratory data analysis (EDA) is an approach of analyzing data sets to summarize their main characteristics, often using statistical graphics and other data visualization methods. A statistical model can be used or not, but primarily EDA is for seeing what the data can tell us beyond the formal modeling and thereby contrasts traditional hypothesis testing. Exploratory data analysis has been promoted by John Tukey since 1970 to encourage statisticians to explore the data, and possibly formulate hypotheses that could lead to new data collection and experiments. EDA is different from initial data analysis (IDA), which focuses more narrowly on checking assumptions required for model fitting and hypothesis testing, and handling missing values and making transformations of variables as needed. EDA encompasses IDA. Overview Tukey defined data analysis in 1961 as: "Procedures for analyzing data, techniques for interpreting the results of such procedures, ways of planni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gustav A
Gustav, Gustaf or Gustave may refer to: *Gustav (name), a male given name of Old Swedish origin Art, entertainment, and media * ''Primeval'' (film), a 2007 American horror film * ''Gustav'' (film series), a Hungarian series of animated short cartoons * Gustav (''Zoids''), a transportation mecha in the ''Zoids'' fictional universe *Gustav, a character in ''Sesamstraße'' *Monsieur Gustav H., a leading character in ''The Grand Budapest Hotel'' Weapons *Carl Gustav recoilless rifle, dubbed "the Gustav" by US soldiers * Schwerer Gustav, 800-mm German siege cannon used during World War II Other uses * Gustav (pigeon), a pigeon of the RAF pigeon service in WWII * Gustave (crocodile), a large male Nile crocodile in Burundi *Gustave, South Dakota *Hurricane Gustav (other), a name used for several tropical cyclones and storms *Gustav, a streetwear clothing brand See also *Gustav of Sweden (other) *Gustav Adolf (other) *Gustave Eiffel (other) * * *Gusta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
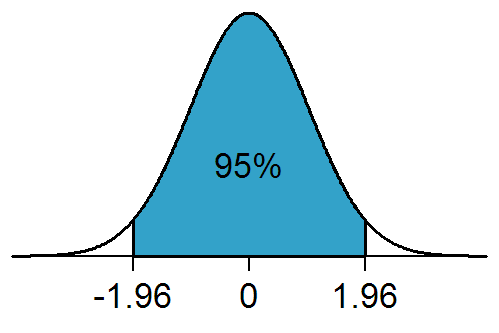
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dichotomy
A dichotomy is a partition of a whole (or a set) into two parts (subsets). In other words, this couple of parts must be * jointly exhaustive: everything must belong to one part or the other, and * mutually exclusive: nothing can belong simultaneously to both parts. If there is a concept A, and it is split into parts B and not-B, then the parts form a dichotomy: they are mutually exclusive, since no part of B is contained in not-B and vice versa, and they are jointly exhaustive, since they cover all of A, and together again give A. Such a partition is also frequently called a bipartition. The two parts thus formed are complements. In logic, the partitions are opposites if there exists a proposition such that it holds over one and not the other. Treating continuous variables or multi categorical variables as binary variables is called dichotomization. The discretization error inherent in dichotomization is temporarily ignored for modeling purposes. Etymology The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistically Independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson's Chi-squared Test
Pearson's chi-squared test (\chi^2) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Test
In statistics, the binomial test is an exact test of the statistical significance of deviations from a theoretically expected distribution of observations into two categories using sample data. Usage The binomial test is useful to test hypotheses about the probability (\pi) of success: : H_0:\pi=\pi_0 where \pi_0 is a user-defined value between 0 and 1. If in a sample of size n there are k successes, while we expect n\pi_0, the formula of the binomial distribution gives the probability of finding this value: : \Pr(X=k)=\binomp^k(1-p)^ If the null hypothesis H_0 were correct, then the expected number of successes would be n\pi_0. We find our p-value for this test by considering the probability of seeing an outcome as, or more, extreme. For a one-tailed test, this is straightforward to compute. Suppose that we want to test if \pi\pi_0 using the summation of the range from k to n instead. Calculating a p-value for a two-tailed test is slightly more complicated, since a binom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bonferroni Correction
In statistics, the Bonferroni correction is a method to counteract the multiple comparisons problem. Background The method is named for its use of the Bonferroni inequalities. An extension of the method to confidence intervals was proposed by Olive Jean Dunn. Statistical hypothesis testing is based on rejecting the null hypothesis if the likelihood of the observed data under the null hypotheses is low. If multiple hypotheses are tested, the probability of observing a rare event increases, and therefore, the likelihood of incorrectly rejecting a null hypothesis (i.e., making a Type I error) increases. The Bonferroni correction compensates for that increase by testing each individual hypothesis at a significance level of \alpha/m, where \alpha is the desired overall alpha level and m is the number of hypotheses. For example, if a trial is testing m = 20 hypotheses with a desired \alpha = 0.05, then the Bonferroni correction would test each individual hypothesis at \alpha = 0.05/20 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holm–Bonferroni Method
In statistics, the Holm–Bonferroni method, also called the Holm method or Bonferroni–Holm method, is used to counteract the problem of multiple comparisons. It is intended to control the family-wise error rate (FWER) and offers a simple test uniformly more powerful than the Bonferroni correction. It is named after Sture Holm, who codified the method, and Carlo Emilio Bonferroni. Motivation When considering several hypotheses, the problem of multiplicity arises: the more hypotheses are checked, the higher the probability of obtaining Type I errors (false positives). The Holm–Bonferroni method is one of many approaches for controlling the FWER, i.e., the probability that one or more Type I errors will occur, by adjusting the rejection criteria for each of the individual hypotheses. Formulation The method is as follows: * Suppose you have m p-values, sorted into order lowest-to-highest P_1,\ldots,P_m, and their corresponding hypotheses H_1,\ldots,H_m(null hypotheses). You ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sture Holm
Sture () was a name borne by three distinct but interrelated noble families in Sweden in the Late Middle Ages and Early Modern Period. It was originally a nickname, meaning 'haughty, proud' (compare the Swedish word ''stursk'' and the Old Norse and Icelandic personal name ''Sturla''), but later became a surname. Particularly famous are the three regents ( sv, riksföreståndare) from these families who ruled Sweden in succession during the fifty-year period between 1470 and 1520, namely: * Sten Sture the Elder, regent 1470–1497 and 1501–1503 * Svante Nilsson, regent 1504–1512 * Sten Sture the Younger, regent 1512–1520 The Sture families are remembered in the names of Sturegatan ('Sture Street') and Stureplan ('Sture Square') in central Stockholm, and by the in Uppsala, as well as , which is produced by a dairy in Sävsjö, close to the main seat of the 'Younger Sture' family at . Sture (Sjöblad) Family The first Sture line to emerge is known in Swedish historiogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scandinavian Journal Of Statistics
The ''Scandinavian Journal of Statistics'' is a quarterly peer-reviewed scientific journal of statistics. It was established in 1974 by four Scandinavian statistical learned societies. It is published by John Wiley & Sons and the editors-in-chief are Sangita Kulathinal (University of Helsinki), Jaakko Peltonen (University of Tampere) and Mikko J. Sillanpää (University of Oulu). According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 1.040, ranking it 97th out of 125 journals in the category "Statistics & Probability". References External links * Wiley (publisher) academic journals Quarterly journals Statistics journals English-language journals Academic journals established in 1974 {{stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
British Journal Of Mathematical And Statistical Psychology
The ''British Journal of Mathematical and Statistical Psychology'' is a British scientific journal founded in 1947. It covers the fields of psychology, statistics, and mathematical psychology. It was established as the ''British Journal of Psychology (Statistical Section)'', was renamed the ''British Journal of Statistical Psychology'' in 1953, and was renamed again to its current title in 1965. Abstracting and indexing The journal is indexed in ''Current Index to Statistics, PsycINFO, Social Sciences Citation Index, Current Contents / Social & Behavioral Sciences, Science Citation Index Expanded, and Scopus Scopus is Elsevier's abstract and citation database launched in 2004. Scopus covers nearly 36,377 titles (22,794 active titles and 13,583 inactive titles) from approximately 11,678 publishers, of which 34,346 are peer-reviewed journals in top-l .... Publications established in 1947 Statistics journals Mathematical and statistical psychology journals Wiley-Blackwel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)