|
Bonferroni Correction
In statistics, the Bonferroni correction is a method to counteract the multiple comparisons problem. Background The method is named for its use of the Bonferroni inequalities. An extension of the method to confidence intervals was proposed by Olive Jean Dunn. Statistical hypothesis testing is based on rejecting the null hypothesis if the likelihood of the observed data under the null hypotheses is low. If multiple hypotheses are tested, the probability of observing a rare event increases, and therefore, the likelihood of incorrectly rejecting a null hypothesis (i.e., making a Type I error) increases. The Bonferroni correction compensates for that increase by testing each individual hypothesis at a significance level of \alpha/m, where \alpha is the desired overall alpha level and m is the number of hypotheses. For example, if a trial is testing m = 20 hypotheses with a desired \alpha = 0.05, then the Bonferroni correction would test each individual hypothesis at \alpha = 0.05/20 = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics In Medicine (journal)
'' Statistics in Medicine'' is a peer-reviewed statistics journal published by Wiley. Established in 1982, the journal publishes articles on medical statistics. The journal is indexed by ''Mathematical Reviews'' and SCOPUS. According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as i ... of 2.497. References External links * Mathematics journals Publications established in 1982 English-language journals Wiley (publisher) academic journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Behavioral Ecology (journal)
''Behavioral Ecology'' is a bimonthly peer-reviewed scientific journal published by Oxford University Press on behalf of the International Society for Behavioral Ecology. The journal was established in 1990. Scope ''Behavioral Ecology'' publishes empirical and theoretical papers on a broad range of topics related to behavioural ecology, including ethology, sociobiology, evolution, and ecology of behaviour. The journal includes research at the levels of the individual, population, and community on various organisms such as vertebrates, invertebrates, and plants. According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 2.671, ranking it 22nd out of 175 journals in the category "Zoology". Artic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
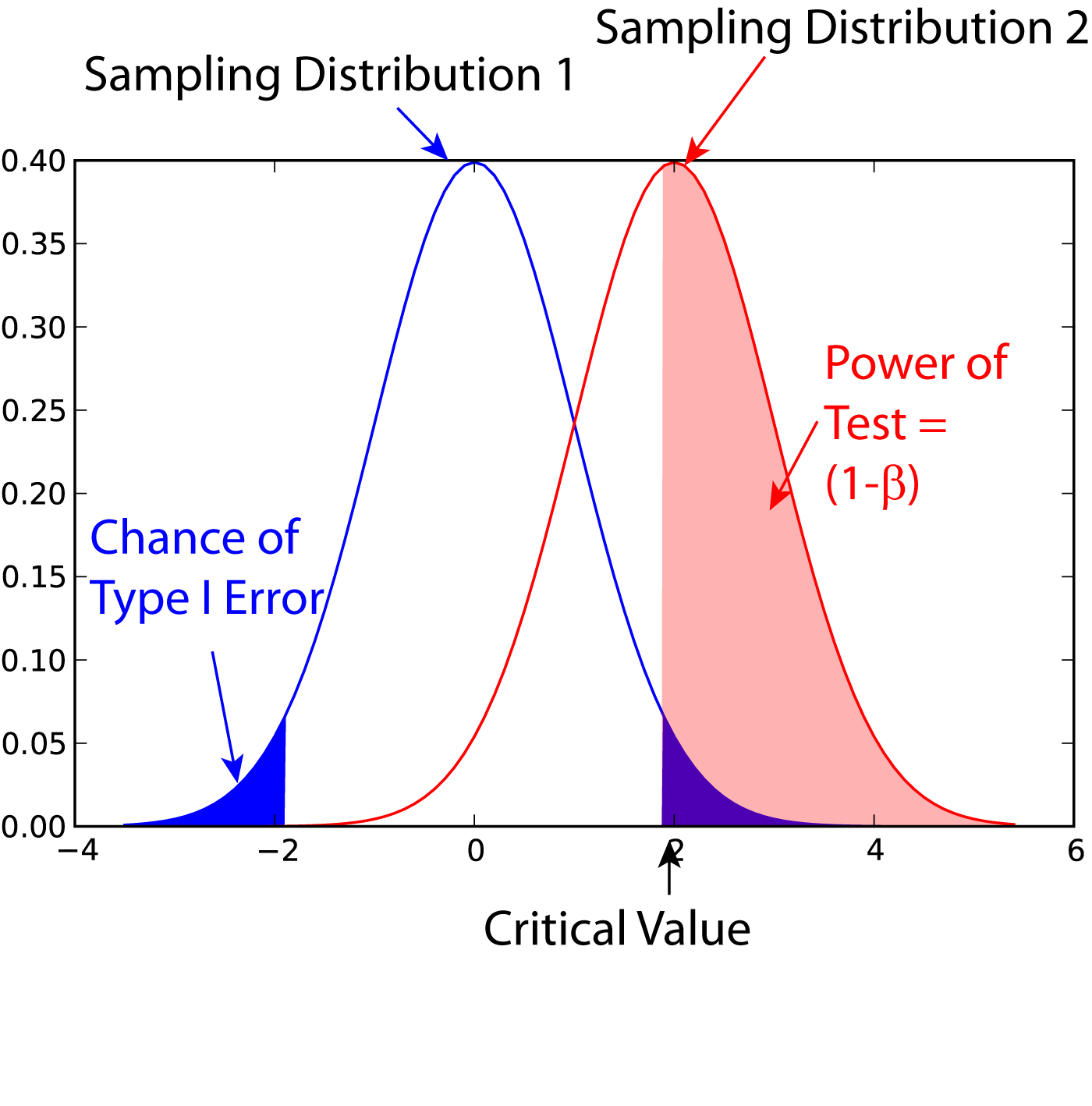
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type I And Type II Errors
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unluck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oikos
The ancient Greek word ''oikos'' (ancient Greek: , plural: ; English prefix: eco- for ecology and economics) refers to three related but distinct concepts: the family, the family's property, and the house. Its meaning shifts even within texts. The ''oikos'' was the basic unit of society in most Greek city-states. In normal Attic usage the ''oikos'', in the context of families, referred to a line of descent from father to son from generation to generation. Alternatively, as Aristotle used it in his ''Politics'', the term was sometimes used to refer to everybody living in a given house. Thus, the head of the ''oikos'', along with his immediate family and his slaves, would all be encompassed. Large ''oikoi'' also had farms that were usually tended by the slaves, which were also the basic agricultural unit of the ancient Greek economy. Layout Traditional interpretations of the layout of the ''oikos'' in Classical Athens have divided into men's and women's spaces, with an area know ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Number
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Šidák Correction
In statistics, the Šidák correction, or Dunn–Šidák correction, is a method used to counteract the problem of multiple comparisons. It is a simple method to control the familywise error rate. When all null hypotheses are true, the method provides familywise error control that is exact for tests that are stochastically independent, is conservative for tests that are positively dependent, and is liberal for tests that are negatively dependent. It is credited to a 1967 paper by the statistician and probabilist Zbyněk Šidák. Usage * Given ''m'' different null hypotheses and a familywise alpha level of \alpha, each null hypotheses is rejected that has a p-value lower than \alpha_ = 1-(1-\alpha)^\frac . * This test produces a familywise Type I error rate of exactly \alpha when the tests are independent from each other and all null hypotheses are true. It is less stringent than the Bonferroni correction, but only slightly. For example, for \alpha = 0.05 and ''m'' = 10, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holm–Bonferroni Method
In statistics, the Holm–Bonferroni method, also called the Holm method or Bonferroni–Holm method, is used to counteract the problem of multiple comparisons. It is intended to control the family-wise error rate (FWER) and offers a simple test uniformly more powerful than the Bonferroni correction. It is named after Sture Holm, who codified the method, and Carlo Emilio Bonferroni. Motivation When considering several hypotheses, the problem of multiplicity arises: the more hypotheses are checked, the higher the probability of obtaining Type I errors (false positives). The Holm–Bonferroni method is one of many approaches for controlling the FWER, i.e., the probability that one or more Type I errors will occur, by adjusting the rejection criteria for each of the individual hypotheses. Formulation The method is as follows: * Suppose you have m p-values, sorted into order lowest-to-highest P_1,\ldots,P_m, and their corresponding hypotheses H_1,\ldots,H_m（null hypotheses). You ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Cosmology And Astroparticle Physics
The ''Journal of Cosmology and Astroparticle Physics'' is an online-only peer-reviewed scientific journal focusing on all aspects of cosmology and astroparticle physics. This encompasses theory, observation, experiment, computation and simulation. It has been published jointly by IOP Publishing and the International School for Advanced Studies The International School for Advanced Studies (Italian: ''Scuola Internazionale Superiore di Studi Avanzati''; SISSA) is an international, state-supported, post-graduate-education and research institute in Trieste, Italy. SISSA is active in the ... since 2003. ''Journal of Cosmology and Astroparticle Physics'' has been a part of the SCOAP3 initiative. But from 1 January 2017 it has moved out from SCOAP3 agreement. Abstracting and indexing ''Journal of Cosmology and Astroparticle Physics'' is indexed and abstracted in the following databases: References External links * Astrophysics journals IOP Publishing academic journa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation that views probability as the limit of the relative frequency of an event after many trials. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can be used to estimate the parameters of a probability distribution or statistical model. Since Bayesian statistics treats probabi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Higgs Boson
The Higgs boson, sometimes called the Higgs particle, is an elementary particle in the Standard Model of particle physics produced by the quantum excitation of the Higgs field, one of the fields in particle physics theory. In the Standard Model, the Higgs particle is a massive scalar boson with zero spin, even (positive) parity, no electric charge, and no colour charge, that couples to (interacts with) mass. It is also very unstable, decaying into other particles almost immediately. The Higgs field is a scalar field, with two neutral and two electrically charged components that form a complex doublet of the weak isospin SU(2) symmetry. Its " Mexican hat-shaped" potential leads it to take a nonzero value ''everywhere'' (including otherwise empty space), which breaks the weak isospin symmetry of the electroweak interaction, and via the Higgs mechanism gives mass to many particles. Both the field and the boson are named after physicist Peter Higgs, who in 1964, along ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
