|
Circumcevian Triangle
In triangle geometry, a circumcevian triangle is a special triangle associated with the reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle. Definition Let P be a point in the plane of the reference triangle ABC. Let the lines AP, BP, CP intersect the circumcircle of triangle ABC at A', B', C'. The triangle A'B'C' is called the circumcevian triangle of P with reference to the triangle ABC. Coordinates Let a,b,c be the side lengths of triangle ABC and let the trilinear coordinates of P be \alpha:\beta:\gamma. Then the trilinear coordinates of the vertices of the circumcevian triangle of P are as follows: :A' (-a\beta\gamma : (b\gamma+c\beta)\beta : (b\gamma+c\beta)\gamma) :B' ((c\alpha +a\gamma)\alpha : - b\gamma\alpha : (c\alpha +a\gamma) \gamma) :C' ((a\beta +b\alpha)\alpha : (a\beta +b\alpha)\beta : - c\alpha\beta) Some properties *Every triangle inscribed in the circumcircle of the reference triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcircle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius. Not every polygon has a circumscribed circle. A polygon that does have one is called a cyclic polygon, or sometimes a concyclic polygon because its vertices are concyclic. All triangles, all regular simple polygons, all rectangles, all isosceles trapezoids, and all right kites are cyclic. A related notion is the one of a minimum bounding circle, which is the smallest circle that completely contains the polygon within it, if the circle's center is within the polygon. Every polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm. Even if a polygon has a circumscribed circle, it may be different from its minimum bounding circle. For example, for an obtuse triangle, the minimum bounding circle has the longes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trilinear Coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is the ratio of the perpendicular distances from the point to the sides (extended if necessary) opposite vertices and respectively; the ratio is the ratio of the perpendicular distances from the point to the sidelines opposite vertices and respectively; and likewise for and vertices and . In the diagram at right, the trilinear coordinates of the indicated interior point are the actual distances (, , ), or equivalently in ratio form, for any positive constant . If a point is on a sideline of the reference triangle, its corresponding trilinear coordinate is 0. If an exterior point is on the opposite side of a sideline from the interior of the triangle, its trilinear coordinate associated with that sideline is negative. It is impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pedal Triangle
In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle. More specifically, consider a triangle ''ABC'', and a point ''P'' that is not one of the vertices ''A, B, C''. Drop perpendiculars from ''P'' to the three sides of the triangle (these may need to be produced, i.e., extended). Label ''L'', ''M'', ''N'' the intersections of the lines from ''P'' with the sides ''BC'', ''AC'', ''AB''. The pedal triangle is then ''LMN''. If ABC is not an obtuse triangle, P is the orthocenter then the angles of LMN are 180°−2A, 180°−2B and 180°−2C. The location of the chosen point ''P'' relative to the chosen triangle ''ABC'' gives rise to some special cases: * If ''P = '' orthocenter, then ''LMN = '' orthic triangle. * If ''P = ''incenter, then ''LMN = ''intouch triangle. * If ''P = '' circumcenter, then ''LMN = '' medial triangle. If ''P'' is on the circumcircle of the triangle, ''LMN'' collapses to a line. This is then called the pedal line, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
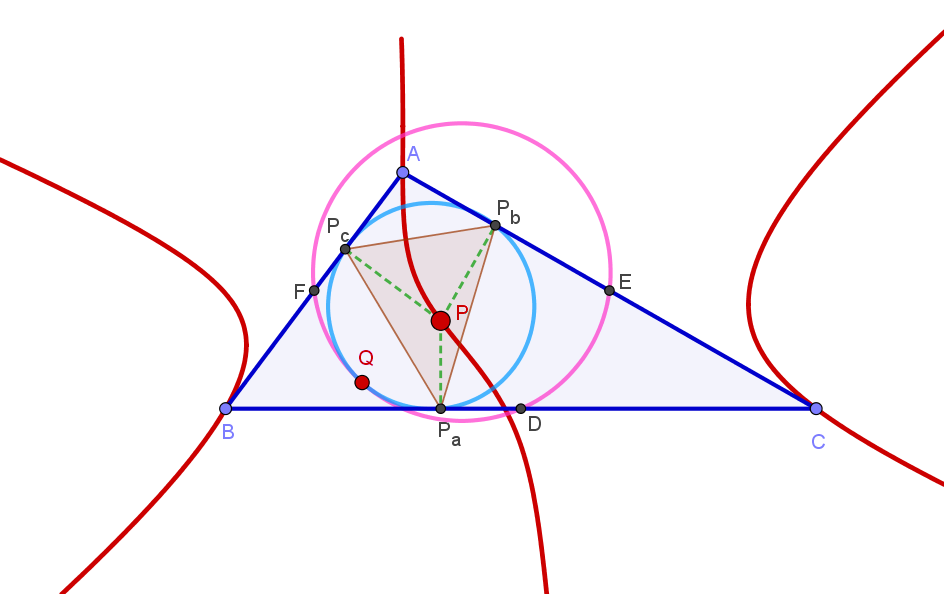
McCay Cubic
In Euclidean geometry, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003. Definition The McCay cubic can be defined by locus properties in several ways. For example, the McCay cubic is the locus of a point such that the pedal circle of is tangent to the nine-point circle of the reference triangle . The McCay cubic can also be defined as the locus of point such that the circumcevian triangle of and are orthologic. Equation of the McCay cubic The equation of the McCay cubic in barycentric coordinates x:y:z is :\sum_(a^2(b^2+c^2-a^2)x(c^2y^2-b^2z^2))=0. The equation in trilinear coordinates \alpha : \beta : \gamma is :\alpha (\beta^2 - \gamma^2)\cos A + \beta (\gamma^2 - \alpha^2)\cos B + \gamma (\alpha^2 - \beta^2)\cos C = 0 McCay cubic as a stelloid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthologic Triangles
In geometry, two triangles are said to be orthologic if the perpendiculars from the vertices of one of them to the corresponding sides of the other are concurrent (i.e., they intersect at a single point). This is a symmetric property; that is, if the perpendiculars from the vertices of triangle to the sides of triangle are concurrent then the perpendiculars from the vertices of to the sides of are also concurrent. The points of concurrence are known as the orthology centres of the two triangles. Some pairs of orthologic triangles The following are some triangles associated with the reference triangle ABC and orthologic with it. * Medial triangle * Anticomplementary triangle * Orthic triangle * The triangle whose vertices are the points of contact of the incircle with the sides of ABC * Tangential triangle * The triangle whose vertices are the points of contacts of the excircles with the respective sides of triangle ABC * The triangle formed by the bisectors of the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cevian
In geometry, a cevian is a line that intersects both a triangle's vertex, and also the side that is opposite to that vertex. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name. Length Stewart's theorem The length of a cevian can be determined by Stewart's theorem: in the diagram, the cevian length is given by the formula :\,b^2m + c^2n = a(d^2 + mn). Less commonly, this is also represented (with some rearrangement) by the following mnemonic: :\underset = \!\!\!\!\!\! \underset Median If the cevian happens to be a median (thus bisecting a side), its length can be determined from the formula :\,m(b^2 + c^2) = a(d^2 + m^2) or :\,2(b^2 + c^2) = 4d^2 + a^2 since :\,a = 2m. Hence in this case :d= \frac\sqrt2 . Angle bisector If the cevian happens to be an angle bisector, its length obeys the formulas :\,(b + c)^2 = a^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ceva's Theorem
In Euclidean geometry, Ceva's theorem is a theorem about triangles. Given a triangle , let the lines be drawn from the vertices to a common point (not on one of the sides of ), to meet opposite sides at respectively. (The segments are known as cevians.) Then, using signed lengths of segments, :\frac \cdot \frac \cdot \frac = 1. In other words, the length is taken to be positive or negative according to whether is to the left or right of in some fixed orientation of the line. For example, is defined as having positive value when is between and and negative otherwise. Ceva's theorem is a theorem of affine geometry, in the sense that it may be stated and proved without using the concepts of angles, areas, and lengths (except for the ratio of the lengths of two line segments that are collinear). It is therefore true for triangles in any affine plane over any field. A slightly adapted converse is also true: If points are chosen on respectively so that : \frac \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |