|
Chvátal Graph
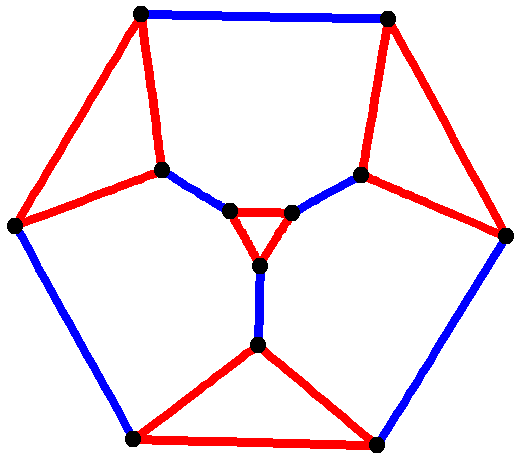
In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic. Coloring, degree, and girth The Chvátal graph is triangle-free: its girth (the length of its shortest cycle) is four. It is 4-regular: each vertex has exactly four neighbors. And its chromatic number is 4: it can be colored using four colors, but not using only three. It is, as Chvátal observes, the smallest possible 4-chromatic 4-regular triangle-free graph; the only smaller 4-chromatic triangle-free graph is the Grötzsch graph, which has 11 vertices but has maximum degree 5 and is not regular. By Brooks’ theorem, every k-regular graph (except for odd cycles and cliques) has chromatic number at most k. It was also known since that, for every k\ge 3 and \ell\ge 3 there exist k-chromatic graphs with girth \ell. In connection with these two resu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '' Ordnung'', meaning the order of approximation. In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; a famous example of such a difference is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates. Big O notation characterizes functions according to their growth rates: d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Graph Theory
The ''Journal of Graph Theory'' is a peer-reviewed mathematics journal specializing in graph theory and related areas, such as structural results about graphs, graph algorithms with theoretical emphasis, and discrete optimization on graphs. The scope of the journal also includes related areas in combinatorics and the interaction of graph theory with other mathematical sciences. It is published by John Wiley & Sons. The journal was established in 1977 by Frank Harary.Frank Harary a biographical sketch at the ACM SIGACT site The are [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Combinatorial Theory
The ''Journal of Combinatorial Theory'', Series A and Series B, are mathematical journals specializing in combinatorics and related areas. They are published by Elsevier. ''Series A'' is concerned primarily with structures, designs, and applications of combinatorics. ''Series B'' is concerned primarily with graph and matroid theory. The two series are two of the leading journals in the field and are widely known as ''JCTA'' and ''JCTB''. The journal was founded in 1966 by Frank Harary and Gian-Carlo Rota.They are acknowledged on the journals' title pages and Web sites. SeEditorial board of JCTA Originally there was only one journal, which was split into two parts in 1971 as the field grew rapidly. An electronic, |
Chromatic Index
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most different colors, for a given value of , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three. By Vizing's theorem, the number of colors needed to edge color a simple graph is either its maximum degree or . For some graphs, such as bipartite graphs and high-degree planar graphs, the number o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence Number
Independence is a condition of a person, nation, country, or Sovereign state, state in which residents and population, or some portion thereof, exercise self-government, and usually sovereignty, over its territory. The opposite of independence is the status of a dependent territory. The commemoration of the independence day of a country or nation celebrates when a country is free from all forms of foreign colonialism; free to build a country or nation without any interference from other nations. Definition of independence Whether the attainment of independence is different from revolution has long been contested, and has often been debated over the question of violence as Legitimacy (family law), legitimate means to achieving sovereignty. In general, revolutions aim only to redistribute power with or without an element of emancipation,such as in democratization ''within'' a state, which as such may remain unaltered. For example, the Mexican Revolution (1910) chiefly refer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tutte Polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph G and contains information about how the graph is connected. It is denoted by T_G. The importance of this polynomial stems from the information it contains about G. Though originally studied in algebraic graph theory as a generalization of counting problems related to graph coloring and nowhere-zero flow, it contains several famous other specializations from other sciences such as the Jones polynomial from knot theory and the partition functions of the Potts model from statistical physics. It is also the source of several central computational problems in theoretical computer science. The Tutte polynomial has several equivalent definitions. It is equivalent to Whitney’s rank polynomial, Tutte’s own dichromatic polynomial and Fortuin–Kasteleyn’ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The characteristic polynomial of an endomorphism of a finite-dimensional vector space is the characteristic polynomial of the matrix of that endomorphism over any base (that is, the characteristic polynomial does not depend on the choice of a basis). The characteristic equation, also known as the determinantal equation, is the equation obtained by equating the characteristic polynomial to zero. In spectral graph theory, the characteristic polynomial of a graph is the characteristic polynomial of its adjacency matrix. Motivation In linear algebra, eigenvalues and eigenvectors play a fundamental role, since, given a linear transformation, an eigenvector is a vector whose direction is not changed by the transformation, and the corresponding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # the problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers to nondeterministic Turing machines, a way of mathematically formalizing the idea of a brute-force search algorithm. Polynomial time refers to an amount of time that is considered "quick" for a det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Cycle
In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs (the Hamiltonian path problem and Hamiltonian cycle problem) are NP-complete. Hamiltonian paths and cycles are named after William Rowan Hamilton who invented the icosian game, now also known as ''Hamilton's puzzle'', which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the icosian calculus, an algebraic structure based on roots of unity with many similarities to the quaternions (also invented by H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automorphism Group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the group of invertible linear transformations from ''X'' to itself (the general linear group of ''X''). If instead ''X'' is a group, then its automorphism group \operatorname(X) is the group consisting of all group automorphisms of ''X''. Especially in geometric contexts, an automorphism group is also called a symmetry group. A subgroup of an automorphism group is sometimes called a transformation group. Automorphism groups are studied in a general way in the field of category theory. Examples If ''X'' is a set with no additional structure, then any bijection from ''X'' to itself is an automorphism, and hence the automorphism group of ''X'' in this case is precisely the symmetric group of ''X''. If the set ''X'' has additional str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex-transitive Graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph in which, given any two vertices and of , there is some automorphism :f : G \to G\ such that :f(v_1) = v_2.\ In other words, a graph is vertex-transitive if its automorphism group acts transitively on its vertices.. A graph is vertex-transitive if and only if its graph complement is, since the group actions are identical. Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's graph). Finite examples Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected cycles) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

%2C_by_John_Trumbull.jpg)