vertex-transitive graph on:
[Wikipedia]
[Google]
[Amazon]
In the
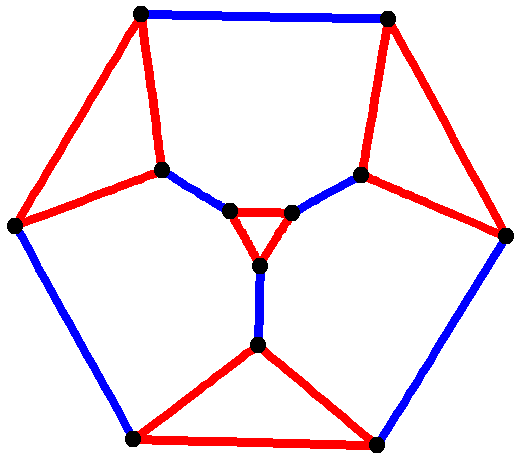 Finite vertex-transitive graphs include the symmetric graphs (such as the
Finite vertex-transitive graphs include the symmetric graphs (such as the
A census of small connected cubic vertex-transitive graphs
Primož Potočnik, Pablo Spiga, Gabriel Verret, 2012.
Vertex-transitive Graphs On Fewer Than 48 Vertices
Gordon Royle and Derek Holt, 2020. Graph families Algebraic graph theory Regular graphs
mathematical
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
field of graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
, an automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphism ...
is a permutation of the vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices and of , there is an automorphism such that
:
In other words, a graph is vertex-transitive if its automorphism group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the g ...
acts transitively on its vertices.. A graph is vertex-transitive if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
its graph complement is, since the group actions are identical.
Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncation (geometry), truncating all 4 vertices of ...
), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's graph).
Finite examples
 Finite vertex-transitive graphs include the symmetric graphs (such as the
Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph i ...
, the Heawood graph and the vertices and edges of the Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
s). The finite Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
s (such as cube-connected cycles) are also vertex-transitive, as are the vertices and edges of the Archimedean solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They ...
s (though only two of these are symmetric). Potočnik, Spiga and Verret have constructed a census of all connected cubic vertex-transitive graphs on at most 1280 vertices.
Although every Cayley graph is vertex-transitive, there exist other vertex-transitive graphs that are not Cayley graphs. The most famous example is the Petersen graph, but others can be constructed including the line graph
In the mathematics, mathematical discipline of graph theory, the line graph of an undirected graph is another graph that represents the adjacencies between edge (graph theory), edges of . is constructed in the following way: for each edge i ...
s of edge-transitive
In geometry, a polytope (for example, a polygon or a polyhedron) or a Tessellation, tiling is isotoxal () or edge-transitive if its Symmetry, symmetries act Transitive group action, transitively on its Edge (geometry), edges. Informally, this mea ...
non- bipartite graphs with odd vertex degrees.
Properties
Theedge-connectivity
In graph theory, a connected Graph (discrete mathematics), graph is -edge-connected if it remains Connectivity (graph theory), connected whenever fewer than edges are removed.
The edge-connectivity of a graph is the largest for which the graph ...
of a connected vertex-transitive graph is equal to the degree ''d'', while the vertex-connectivity will be at least 2(''d'' + 1)/3.
If the degree is 4 or less, or the graph is also edge-transitive
In geometry, a polytope (for example, a polygon or a polyhedron) or a Tessellation, tiling is isotoxal () or edge-transitive if its Symmetry, symmetries act Transitive group action, transitively on its Edge (geometry), edges. Informally, this mea ...
, or the graph is a minimal Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
, then the vertex-connectivity will also be equal to ''d''.
Infinite examples
Infinite vertex-transitive graphs include: * infinite paths (infinite in both directions) * infinite regulartrees
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, e.g., including only woody plants with secondary growth, only p ...
, e.g. the Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
of the free group
In mathematics, the free group ''F'S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''− ...
* graphs of uniform tessellations (see a complete list of planar tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety ...
s), including all tilings by regular polygons
* infinite Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
s
* the Rado graph
In the mathematics, mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a Countable set, countably infinite graph that can be constructed (with probability one) by choosing independently at random for eac ...
Two countable
In mathematics, a Set (mathematics), set is countable if either it is finite set, finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function fro ...
vertex-transitive graphs are called quasi-isometric if the ratio of their distance functions is bounded from below and from above. A well known conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
stated that every infinite vertex-transitive graph is quasi-isometric to a Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
. A counterexample was proposed by Diestel and Leader
Leadership, is defined as the ability of an individual, group, or organization to "", influence, or guide other individuals, teams, or organizations.
"Leadership" is a contested term. Specialist literature debates various viewpoints on the co ...
in 2001. In 2005, Eskin, Fisher, and Whyte confirmed the counterexample..
See also
*Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph such that, given any two edges and of , there is an automorphism of that maps to .
In other words, a graph is edge-transitive if its automorphism group acts t ...
* Lovász conjecture
* Semi-symmetric graph
* Zero-symmetric graph
References
External links
* {{MathWorld , urlname=Vertex-TransitiveGraph , title=Vertex-transitive graphA census of small connected cubic vertex-transitive graphs
Primož Potočnik, Pablo Spiga, Gabriel Verret, 2012.
Vertex-transitive Graphs On Fewer Than 48 Vertices
Gordon Royle and Derek Holt, 2020. Graph families Algebraic graph theory Regular graphs