|
Chapman–Enskog Theory
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one. The theory is named for Sydney Chapman and David Enskog, who introduced it independently in 1916 and 1917. Description The starting point of Chapman–Enskog theory is the Boltzmann equation for the 1-particle distribution function f(\mathbf,\mathbf,t): : \frac+\mathbf\frac+\frac \cdot\frac=\hat f, where \hat is a nonlinear integral operator which models the evolution of f under interp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Equation
In mathematics, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,...,x_n ; u(x_1,x_2,x_3,...,x_n) ; I^1 (u), I^2(u), I^3(u), ..., I^m(u)) = 0where I^i(u) is an integral operator acting on ''u.'' Hence, integral equations may be viewed as the analog to differential equations where instead of the equation involving derivatives, the equation contains integrals. A direct comparison can be seen with the mathematical form of the general integral equation above with the general form of a differential equation which may be expressed as follows:f(x_1,x_2,x_3,...,x_n ; u(x_1,x_2,x_3,...,x_n) ; D^1 (u), D^2(u), D^3(u), ..., D^m(u)) = 0where D^i(u) may be viewed as a differential operator of order ''i''. Due to this close connection between differential and integral equations, one can often convert between the two. For example, one method of so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Theory Of Gases
Kinetic (Ancient Greek: κίνησις “kinesis”, movement or to move) may refer to: * Kinetic theory, describing a gas as particles in random motion * Kinetic energy In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its a ..., the energy of an object that it possesses due to its motion Art and entertainment * Kinetic art, a form of art involving mechanical and/or random movement, including optical illusions. * ''Kinetic'', the 13th episode of the first season of the TV series ''Smallville'' * ''Kinetic'' (comics), a comic by Allan Heinberg and Kelley Pucklett * "Kinetic" (song), a song by Radiohead Companies * Kinetic Engineering Limited, Indian automotive manufacturer * Kinetic Group, Australian-based public transport company Technology * "Kinetic", Seiko's trademark for its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noble Gas
The noble gases (historically also the inert gases; sometimes referred to as aerogens) make up a class of chemical elements with similar properties; under standard conditions, they are all odorless, colorless, monatomic gases with very low chemical reactivity. The six naturally occurring noble gases are helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), and the radioactive radon (Rn). Oganesson (Og) is a synthetically produced highly radioactive element. Although IUPAC has used the term "noble gas" interchangeably with "group 18" and thus included oganesson, it may not be significantly chemically noble and is predicted to break the trend and be reactive due to relativistic effects. Because of the extremely short 0.7 ms half-life of its only known isotope, its chemistry has not yet been investigated. For the first six periods of the periodic table, the noble gases are exactly the members of group 18. Noble gases are typically highly unreactive excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell Molecule
Maxwell may refer to: People * Maxwell (surname), including a list of people and fictional characters with the name ** James Clerk Maxwell, mathematician and physicist * Justice Maxwell (other) * Maxwell baronets, in the Baronetage of Nova Scotia * Maxwell (footballer, born 1979), Brazilian forward * Maxwell (footballer, born 1981), Brazilian left-back * Maxwell (footballer, born 1986), Brazilian striker * Maxwell (footballer, born 1989), Brazilian left-back * Maxwell (footballer, born 1995), Brazilian forward * Maxwell (musician) (born 1973), American R&B and neo-soul singer * Maxwell (rapper) (born 1993), German rapper, member of rap band 187 Strassenbande * Maxwell Jacob Friedman (born 1997) AEW Professional wrestler * Maxwell Silva (born 1953), Sri Lankan Sinhala Catholic cleric, Auxiliary Bishop of Colombo Places United States * Maxwell, California * Maxwell, Indiana * Maxwell, Iowa * Maxwell, Nebraska * Maxwell, New Mexico * Maxwell, Texas * Maxwell Air Forc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
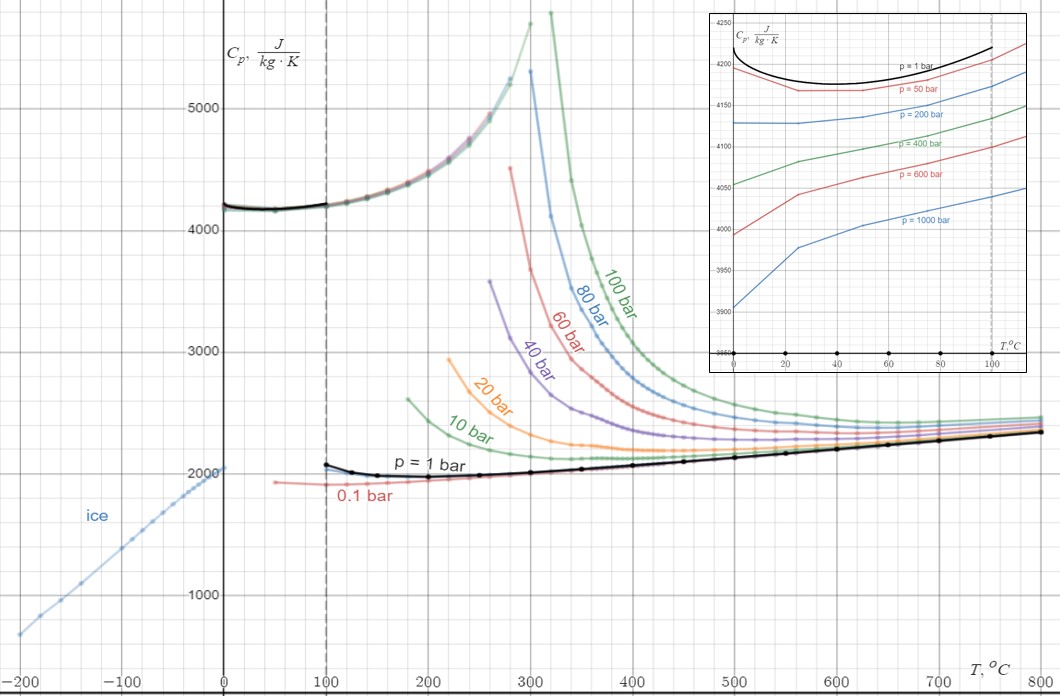
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably dependin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish mathematician and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the " second great unification in physics" where the first one had been realised by Isaac Newton. With the publication of " A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society. His statement that "light and magnetism are affections of the same substance" is at page 499.) The unification of light and electri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lennard-Jones Potential
The Lennard-Jones potential (also termed the LJ potential or 12-6 potential) is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential models soft repulsive and attractive ( van der Waals) interactions. Hence, the Lennard-Jones potential describes electronically neutral atoms or molecules. It is named after John Lennard-Jones. The commonly used expression for the Lennard-Jones potential is V_\text(r) = 4\varepsilon \left \left(\frac\right)^ - \left(\frac\right)^6 \right, where r is the distance between two interacting particles, \varepsilon is the depth of the potential well (usually referred to as 'dispersion energy'), and \sigma is the distance at which the particle-particle potential energy V is zero (often referred to as 'size of the particle'). Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newtonian Fluid
A Newtonian fluid is a fluid in which the viscous stress tensor, viscous stresses arising from its Fluid dynamics, flow are at every point linearly correlated to the local strain rate — the derivative (mathematics), rate of change of its deformation (mechanics), deformation over time. Stresses are proportional to the rate of change of the fluid's velocity, velocity vector. A fluid is Newtonian only if the tensors that describe the viscous stress and the strain rate are related by a constant viscosity, viscosity tensor that does not depend on the stress state and velocity of the flow. If the fluid is also isotropic (mechanical properties are the same along any direction), the viscosity tensor reduces to two real coefficients, describing the fluid's resistance to continuous Shearing (physics), shear deformation and continuous compression (physical), compression or expansion, respectively. Newtonian fluids are the simplest mathematical models of fluids that account for viscosity. W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |