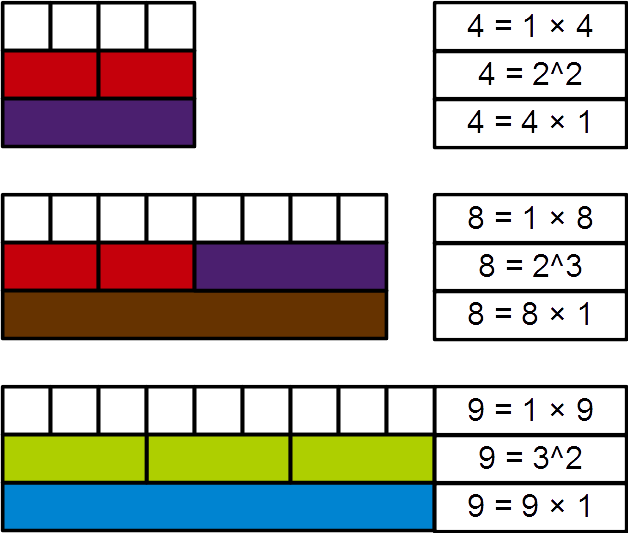
|
Catalan's Conjecture
Catalan's conjecture (or Mihăilescu's theorem) is a theorem in number theory that was Conjecture, conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu at Paderborn University. The integers 23 and 32 are two perfect powers (that is, powers of exponent higher than one) of natural numbers whose values (8 and 9, respectively) are consecutive. The theorem states that this is the ''only'' case of two consecutive perfect powers. That is to say, that History The history of the problem dates back at least to Gersonides, who proved a special case of the conjecture in 1343 where (''x'', ''y'') was restricted to be (2, 3) or (3, 2). The first significant progress after Catalan made his conjecture came in 1850 when Victor-Amédée Lebesgue dealt with the case ''b'' = 2. In 1976, Robert Tijdeman applied Baker's method in transcendental number theory, transcendence theory to establish a bound on a,b and used existing results bounding '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In the mainstream of mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice, or of a less powerful theory, such as Peano arithmetic. A notable exception is Wiles's proof of Fermat's Last Theorem, which involves the Grothendieck universes whose existence requires the addition of a new axiom to the set theory. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclotomic Field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex root of unity to , the field of rational numbers. Cyclotomic fields played a crucial role in the development of modern algebra and number theory because of their relation with Fermat's Last Theorem. It was in the process of his deep investigations of the arithmetic of these fields (for prime ) – and more precisely, because of the failure of unique factorization in their rings of integers – that Ernst Kummer first introduced the concept of an ideal number and proved his celebrated congruences. Definition For , let ; this is a primitive th root of unity. Then the th cyclotomic field is the extension of generated by . Properties * The th cyclotomic polynomial : \Phi_n(x) = \!\!\!\prod_\stackrel\!\!\! \left(x-e^\right) = \!\!\!\prod_\stackrel\!\!\! (x-^k) :is irreducible, so it is the minimal polynomial of over . * The conjugates of in are therefore the other primiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tijdeman's Theorem
In number theory, Tijdeman's theorem states that there are at most a finite number of consecutive powers. Stated another way, the set of solutions in integers ''x'', ''y'', ''n'', ''m'' of the exponential diophantine equation :y^m = x^n + 1, for exponents ''n'' and ''m'' greater than one, is finite. History The theorem was proven by Dutch number theorist Robert Tijdeman in 1976, making use of Baker's method in transcendental number theory to give an effective upper bound for ''x'',''y'',''m'',''n''. Michel Langevin computed a value of exp exp exp exp 730 for the bound. Tijdeman's theorem provided a strong impetus towards the eventual proof of Catalan's conjecture by Preda Mihăilescu. Mihăilescu's theorem states that there is only one member to the set of consecutive power pairs, namely 9=8+1. Generalized Tijdeman problem That the powers are consecutive is essential to Tijdeman's proof; if we replace the difference of ''1'' by any other difference ''k'' and ask for the numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Størmer's Theorem
In number theory, Størmer's theorem, named after Carl Størmer, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations. It follows from the Thue–Siegel–Roth theorem that there are only a finite number of pairs of this type, but Størmer gave a procedure for finding them all. Statement If one chooses a finite set P=\ of prime numbers then the -smooth numbers are defined as the set of integers :\left\ that can be generated by products of numbers in . Then Størmer's theorem states that, for every choice of , there are only finitely many pairs of consecutive -smooth numbers. Further, it gives a method of finding them all using Pell equations. The procedure Størmer's original procedure involves solving a set of roughly 3''k'' Pell equations, in each one finding only the smallest solution. A simplified version of the procedure, due to D. H. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ramanujan–Nagell Equation
In mathematics, in the field of number theory, the Ramanujan–Nagell equation is an equation between a square number and a number that is seven less than a power of two. It is an example of an exponential Diophantine equation, an equation to be solved in integers where one of the variables appears as an exponent. The equation is named after Srinivasa Ramanujan, who conjectured that it has only five integer solutions, and after Trygve Nagell, who proved the conjecture. It implies non-existence of perfect binary codes with the minimum Hamming distance 5 or 6. Equation and solution The equation is :2^n-7=x^2 \, and solutions in natural numbers ''n'' and ''x'' exist just when ''n'' = 3, 4, 5, 7 and 15 . This was conjectured in 1913 by Indian mathematician Srinivasa Ramanujan, proposed independently in 1943 by the Norwegian mathematician Wilhelm Ljunggren, and proved in 1948 by the Norwegian mathematician Trygve Nagell. The values of ''n'' correspond to the values of ''x'' as:- :'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mordell Curve
In algebra, a Mordell curve is an elliptic curve of the form ''y''2 = ''x''3 + ''n'', where ''n'' is a fixed non-zero integer. These curves were closely studied by Louis Mordell, from the point of view of determining their integer points. He showed that every Mordell curve contains only finitely many integer points (''x'', ''y''). In other words, the differences of perfect squares and perfect cubes tend to infinity. The question of how fast was dealt with in principle by Baker's method. Hypothetically this issue is dealt with by Marshall Hall's conjecture In mathematics, Hall's conjecture is an open question, , on the differences between perfect squares and perfect cubes. It asserts that a perfect square ''y''2 and a perfect cube ''x''3 that are not equal must lie a substantial distance apart. This .... Properties If (''x'', ''y'') is an integer point on a Mordell curve, then so is (''x'', ''-y''). There are certain values of ''n'' for which the corresponding Mordell curve has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat–Catalan Conjecture
In number theory, the Fermat–Catalan conjecture is a generalization of Fermat's Last Theorem and of Catalan's conjecture, hence the name. The conjecture states that the equation has only finitely many solutions (''a'',''b'',''c'',''m'',''n'',''k'') with distinct triplets of values (''a''''m'', ''b''''n'', ''c''''k'') where ''a'', ''b'', ''c'' are positive coprime integers and ''m'', ''n'', ''k'' are positive integers satisfying The inequality on ''m'', ''n'', and ''k'' is a necessary part of the conjecture. Without the inequality there would be infinitely many solutions, for instance with ''k'' = 1 (for any ''a'', ''b'', ''m'', and ''n'' and with ''c'' = ''a''''m'' + ''b''''n'') or with ''m'', ''n'', and ''k'' all equal to two (for the infinitely many known Pythagorean triples). Known solutions As of 2015, the following ten solutions to equation (1) which meet the criteria of equation (2) are known:. :1^m+2^3=3^2\; (for m>6 to satisfy Eq. 2) :2^5+7^2=3^4\; :7^3+13^2=2^9\; : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation X^y = Y^x
In general, exponentiation fails to be commutative. However, the equation x^y = y^x holds in special cases, such as x=2,\ y=4. History The equation x^y=y^x is mentioned in a letter of Bernoulli to Goldbach (29 June 1728). The letter contains a statement that when x\ne y, the only solutions in natural numbers are (2, 4) and (4, 2), although there are infinitely many solutions in rational numbers, such as (\tfrac, \tfrac) and (\tfrac, \tfrac). The reply by Goldbach (31 January 1729) contains general solution of the equation, obtained by substituting y=vx. A similar solution was found by Euler. J. van Hengel pointed out that if r, n are positive integers with r \geq 3, then r^ > (r+n)^r; therefore it is enough to consider possibilities x = 1 and x = 2 in order to find solutions in natural numbers. The problem was discussed in a number of publications. In 1960, the equation was among the questions on the William Lowell Putnam Competition, which prompted Alvin Hausner to extend re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beal's Conjecture
The Beal conjecture is the following conjecture in number theory: :If :: A^x +B^y = C^z, :where ''A'', ''B'', ''C'', ''x'', ''y'', and ''z'' are positive integers with ''x'', ''y'', ''z'' ≥ 3, then ''A'', ''B'', and ''C'' have a common prime factor. Equivalently, :The equation A^x + B^y = C^z has no solutions in positive integers and pairwise coprime integers ''A, B, C'' if ''x, y, z'' ≥ 3. The conjecture was formulated in 1993 by Andrew Beal, a banker and amateur mathematician, while investigating generalizations of Fermat's Last Theorem. Since 1997, Beal has offered a monetary prize for a peer-reviewed proof of this conjecture or a counterexample. The value of the prize has increased several times and is currently $1 million. In some publications, this conjecture has occasionally been referred to as a generalized Fermat equation, the Mauldin conjecture, and the Tijdeman-Zagier conjecture. Related examples To illustrate, the solution 3^3 + 6^3 = 3^5 has bases with a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Erdős
Paul Erdős ( hu, Erdős Pál ; 26 March 1913 – 20 September 1996) was a Hungarian mathematician. He was one of the most prolific mathematicians and producers of mathematical conjectures of the 20th century. pursued and proposed problems in discrete mathematics, graph theory, number theory, mathematical analysis, approximation theory, set theory, and probability theory. Much of his work centered around discrete mathematics, cracking many previously unsolved problems in the field. He championed and contributed to Ramsey theory, which studies the conditions in which order necessarily appears. Overall, his work leaned towards solving previously open problems, rather than developing or exploring new areas of mathematics. Erdős published around 1,500 mathematical papers during his lifetime, a figure that remains unsurpassed. He firmly believed mathematics to be a social activity, living an itinerant lifestyle with the sole purpose of writing mathematical papers with other mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ABC Conjecture
The ''abc'' conjecture (also known as the Oesterlé–Masser conjecture) is a conjecture in number theory that arose out of a discussion of Joseph Oesterlé and David Masser in 1985. It is stated in terms of three positive integers ''a'', ''b'' and ''c'' (hence the name) that are relatively prime and satisfy ''a'' + ''b'' = ''c''. The conjecture essentially states that the product of the distinct prime factors of ''abc'' is usually not much smaller than ''c''. A number of famous conjectures and theorems in number theory would follow immediately from the ''abc'' conjecture or its versions. Mathematician Dorian Goldfeld described the ''abc'' conjecture as "The most important unsolved problem in Diophantine analysis". The ''abc'' conjecture originated as the outcome of attempts by Oesterlé and Masser to understand the Szpiro conjecture about elliptic curves, which involves more geometric structures in its statement than the ''abc'' conjecture. The ''abc'' conjecture was sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.PNG "Click for more on -> Theorem")
