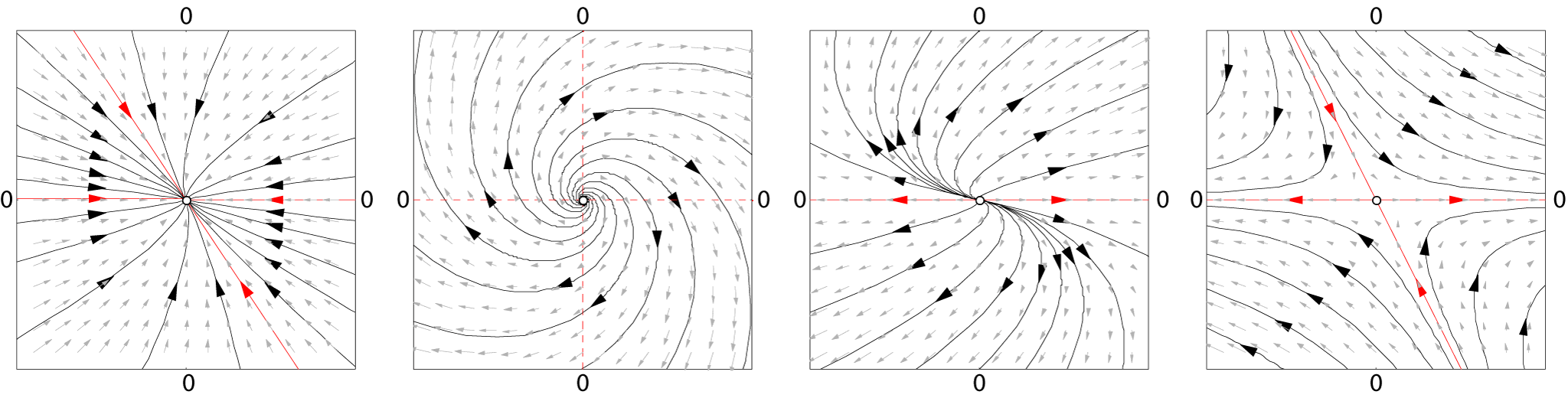
|
Carleman Linearization
In mathematics, Carleman linearization (or Carleman embedding) is a technique to transform a finite-dimensional nonlinear dynamical system into an infinite-dimensional linear system. It was introduced by the Swedish mathematician Torsten Carleman in 1932. Carleman linearization is related to composition operator and has been widely used in the study of dynamical systems. It also been used in many applied fields, such as in control theory and in quantum computing. Procedure Consider the following autonomous nonlinear system: : \dot=f(x)+\sum_^m g_j(x)d_j(t) where x\in R^n denotes the system state vector. Also, f and g_i's are known analytic vector functions, and d_j is the j^ element of an unknown disturbance to the system. At the desired nominal point, the nonlinear functions in the above system can be approximated by Taylor expansion : f(x)\simeq f(x_0)+ \sum _^\eta \frac\partial f_\mid _(x-x_0)^ where \partial f_\mid _ is the k^ partial derivative of f(x) with respect t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsten Carleman
Torsten Carleman (8 July 1892, Visseltofta, Osby Municipality – 11 January 1949, Stockholm), born Tage Gillis Torsten Carleman, was a Swedish mathematician, known for his results in classical analysis and its applications. As the director of the Mittag-Leffler Institute for more than two decades, Carleman was the most influential mathematician in Sweden. Work The dissertation of Carleman under Erik Albert Holmgren, as well as his work in the early 1920s, was devoted to singular integral equations. He developed the spectral theory of integral operators with ''Carleman kernels'', that is, kernels ''K''(''x'', ''y'') such that ''K''(''y'', ''x'') = for almost every (''x'', ''y''), and : \int , K(x, y) , ^2 dy < \infty for almost every ''x''. In the mid-1920s, Carleman developed the theory of |
Composition Operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the rule C_\phi (f) = f \circ \phi where f \circ \phi denotes function composition. The study of composition operators is covered bAMS category 47B33 In physics In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman operator (and its wild surge in popularity is sometimes jokingly called "Koopmania"), named after Bernard Koopman. It is the left-adjoint of the transfer operator of Frobenius–Perron. In Borel functional calculus Using the language of category theory, the composition operator is a pull-back on the space of measurable functions; it is adjoint to the transfer operator in the same way that the pull-back is adjoint to the push-forward; the composition operator is the inverse image functor. Since the domain considered here is that of Borel functions, the above describes the Koopman operator as it appears in B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control system eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though current quantum computers may be too small to outperform usual (classical) computers for practical applications, larger realizations are believed to be capable of solving certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science. There are several models of quantum computation with the most widely used being quantum circuits. Other models include the quantum Turing machine, quantum annealing, and adiabatic quantum computation. Most models are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. A qubit can be in a 1 or 0 quantum s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carleman Matrix
In mathematics, a Carleman matrix is a matrix used to convert function composition into matrix multiplication. It is often used in iteration theory to find the continuous iteration of functions which cannot be iterated by pattern recognition alone. Other uses of Carleman matrices occur in the theory of probability generating functions, and Markov chains. Definition The Carleman matrix of an infinitely differentiable function f(x) is defined as: :M = \frac\left frac (f(x))^j \right ~, so as to satisfy the (Taylor series) equation: :(f(x))^j = \sum_^ M x^k. For instance, the computation of f(x) by :f(x) = \sum_^ M x^k. ~ simply amounts to the dot-product of row 1 of M with a column vector \left ,x,x^2,x^3,...\right\tau. The entries of M /math> in the next row give the 2nd power of f(x): :f(x)^2 = \sum_^ M x^k ~, and also, in order to have the zeroth power of f(x) in M /math>, we adopt the row 0 containing zeros everywhere except the first position, such that :f(x)^0 = 1 = \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composition Operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the rule C_\phi (f) = f \circ \phi where f \circ \phi denotes function composition. The study of composition operators is covered bAMS category 47B33 In physics In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman operator (and its wild surge in popularity is sometimes jokingly called "Koopmania"), named after Bernard Koopman. It is the left-adjoint of the transfer operator of Frobenius–Perron. In Borel functional calculus Using the language of category theory, the composition operator is a pull-back on the space of measurable functions; it is adjoint to the transfer operator in the same way that the pull-back is adjoint to the push-forward; the composition operator is the inverse image functor. Since the domain considered here is that of Borel functions, the above describes the Koopman operator as it appears in B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Igor Mezić
Igor Mezić is a mechanical engineer, mathematician, and Distinguished Professor of mechanical engineering and mathematics at the University of California, Santa Barbara. He is best known for his contributions to operator theoretic, data driven approach to dynamical systems theory that he advanced via articles based on Koopman operator theory, and his work on theory of mixing, that culminated in work on microfluidic mixer design, and mapping oil refuse from the ''Deepwater Horizon'' oil spill in the Gulf of Mexico to aid in cleaning efforts. He graduated from the Mechanical Engineering Department at University of Rijeka, Croatia in 1990, with a Diploma in Engineering, and got the Ph.D. degree from the California Institute of Technology (Caltech), within the Applied Mechanics program, with a thesis in Dynamical Systems Theory, in 1994, under supervision of Stephen R. Wiggins. Mezić was a postdoctoral fellow at the Mathematics Institute of the University of Warwick in the UK f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functions And Mappings
In mathematics, a map or mapping is a function in its general sense. These terms may have originated as from the process of making a geographical map: ''mapping'' the Earth surface to a sheet of paper. The term ''map'' may be used to distinguish some special types of functions, such as homomorphisms. For example, a linear map is a homomorphism of vector spaces, while the term linear function may have this meaning or it may mean a linear polynomial. In category theory, a map may refer to a morphism. The term ''transformation'' can be used interchangeably, but ''transformation'' often refers to a function from a set to itself. There are also a few less common uses in logic and graph theory. Maps as functions In many branches of mathematics, the term ''map'' is used to mean a function, sometimes with a specific property of particular importance to that branch. For instance, a "map" is a "continuous function" in topology, a "linear transformation" in linear algebra, etc. Some au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Quantum Computing")
