|
CaRMetal
CaRMetal is an interactive geometry program which inherited the C.a.R. engine. The software has been created by Eric Hakenholz, in Java. CaRMetal is free, under GNU GPL license. It keeps an amount of functionality of C.a.R. but uses a different graphical interface which purportedly eliminates some intermediate dialogs and provides direct access to numerous effects. Constructions are done using a main palette, which contains some useful construction shortcuts in addition to the standard compass and ruler tools. These include perpendicular bisector, circle through three points, circumcircular arc through three points, and conic section through five points. Also interesting are the loci, functions, parametric curves, and implicit plots. Element thickness, color, label, and other attributes (including the so-called magnetic property) can be set using a separate panel. CaRMetal also supports a configurable restricted construction palette and has assignment capabilities, which use an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interactive Geometry Software
Interactive geometry software (IGS) or dynamic geometry environments (DGEs) are computer programs which allow one to create and then manipulate geometric constructions, primarily in plane geometry. In most IGS, one starts construction by putting a few points and using them to define new objects such as lines, circles or other points. After some construction is done, one can move the points one started with and see how the construction changes. History The earliest IGS was the Geometric Supposer, which was developed in the early 1980s. This was soon followed by Cabri in 1986 and The Geometer's Sketchpad. Comparison There are three main types of computer environments for studying school geometry: supposers, dynamic geometry environments (DGEs) and Logo-based programs. Most are DGEs: software that allows the user to manipulate ("drag") the geometric object into different shapes or positions. The main example of a supposer is the Geometric Supposer, which does not have draggable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Interactive Geometry Software
Interactive geometry software (IGS) or dynamic geometry environments (DGEs) are computer programs which allow one to create and then manipulate geometric constructions, primarily in plane geometry. In most IGS, one starts construction by putting a few points and using them to define new objects such as lines, circles or other points. After some construction is done, one can move the points one started with and see how the construction changes. History The earliest IGS was the Geometric Supposer, which was developed in the early 1980s. This was soon followed by Cabri in 1986 and The Geometer's Sketchpad. Comparison There are three main types of computer environments for studying school geometry: supposers, dynamic geometry environments (DGEs) and Logo-based programs. Most are DGEs: software that allows the user to manipulate ("drag") the geometric object into different shapes or positions. The main example of a supposer is the Geometric Supposer, which does not have draggable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Java (programming Language)
Java is a high-level, class-based, object-oriented programming language that is designed to have as few implementation dependencies as possible. It is a general-purpose programming language intended to let programmers ''write once, run anywhere'' ( WORA), meaning that compiled Java code can run on all platforms that support Java without the need to recompile. Java applications are typically compiled to bytecode that can run on any Java virtual machine (JVM) regardless of the underlying computer architecture. The syntax of Java is similar to C and C++, but has fewer low-level facilities than either of them. The Java runtime provides dynamic capabilities (such as reflection and runtime code modification) that are typically not available in traditional compiled languages. , Java was one of the most popular programming languages in use according to GitHub, particularly for client–server web applications, with a reported 9 million developers. Java was originally developed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DrGeo
GNU Dr. Geo is interactive geometry software that allows its users to design & manipulate interactive geometric sketches. It is free software (source code, translations, icons and installer are released under GNU GPL license), created by Hilaire Fernandes, it is part of the GNU project. It runs over a Morphic graphic system (which means that it runs on Linux, Mac OS, Windows, Android). Current version of Dr. Geo is also called Dr. Geo II. Historically Dr. Geo was developed in C++ and Dr. Geo II is a complete rewrite using Pharo that happened in 2005. This article refers to the most recent version. Objects Dr. Geo manipulates different kinds of objects such as points, lines, circles, block of code. Points Dr. Geo has several kinds of points: a free point, which can be moved with the mouse (but may be attached to a curve) and a point given by its coordinates. Points can also be created as the intersection of 2 curves or as the midpoint of a segment. Lines Dr. Geo is equippe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Geometry
Finite is the opposite of infinite. It may refer to: * Finite number (other) * Finite set, a set whose cardinality (number of elements) is some natural number * Finite verb, a verb form that has a subject, usually being inflected or marked for person and/or tense or aspect * "Finite", a song by Sara Groves from the album '' Invisible Empires'' See also * * Nonfinite (other) Nonfinite is the opposite of finite * a nonfinite verb is a verb that is not capable of serving as the main verb in an independent clause * a non-finite clause In linguistics, a non-finite clause is a dependent or embedded clause that represen ... {{disambiguation fr:Fini it:Finito ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pixel
In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a raster image, or the smallest point in an all points addressable display device. In most digital display devices, pixels are the smallest element that can be manipulated through software. Each pixel is a sample of an original image; more samples typically provide more accurate representations of the original. The intensity of each pixel is variable. In color imaging systems, a color is typically represented by three or four component intensities such as red, green, and blue, or cyan, magenta, yellow, and black. In some contexts (such as descriptions of camera sensors), ''pixel'' refers to a single scalar element of a multi-component representation (called a ''photosite'' in the camera sensor context, although ''sensel'' is sometimes used), while in yet other contexts (like MRI) it may refer to a set of component intensities for a spatial position. Etymology The w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinates (mathematics)
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or ''barycenter'') of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex. Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity. Barycentric coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diamond
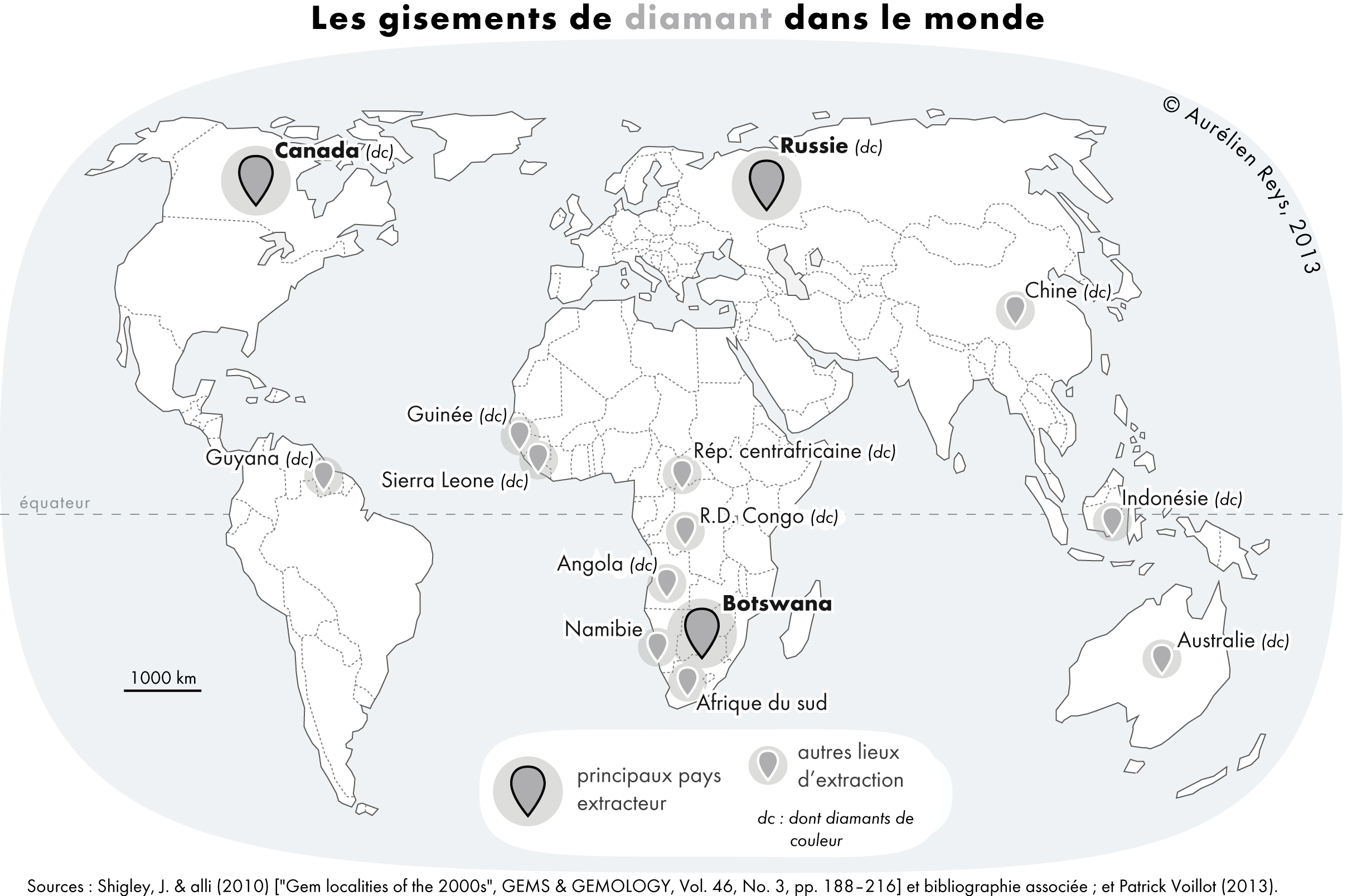
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Another solid form of carbon known as graphite is the Chemical stability, chemically stable form of carbon at Standard conditions for temperature and pressure, room temperature and pressure, but diamond is metastable and converts to it at a negligible rate under those conditions. Diamond has the highest Scratch hardness, hardness and thermal conductivity of any natural material, properties that are used in major industrial applications such as cutting and polishing tools. They are also the reason that diamond anvil cells can subject materials to pressures found deep in the Earth. Because the arrangement of atoms in diamond is extremely rigid, few types of impurity can contaminate it (two exceptions are boron and nitrogen). Small numbers of lattice defect, defects or impurities (about one per million of lattice atoms) color diamond blue (bor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_waving.svg "Click for more on -> Java (programming Language)")
