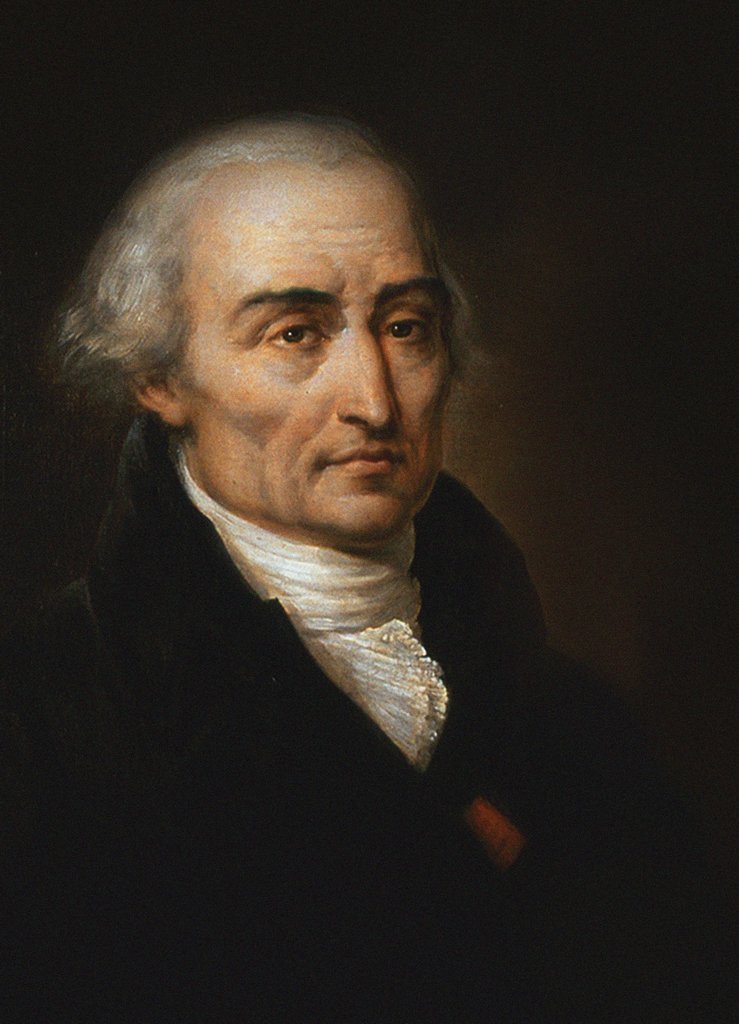|
Brachistochrone
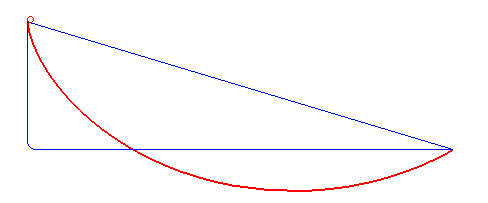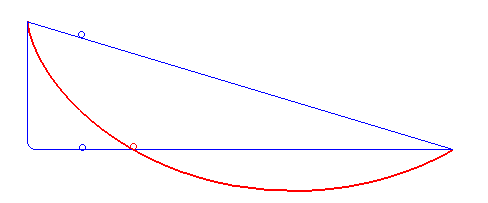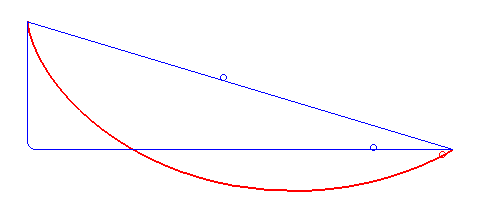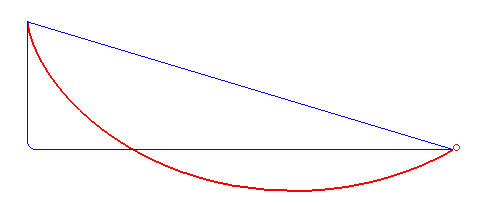
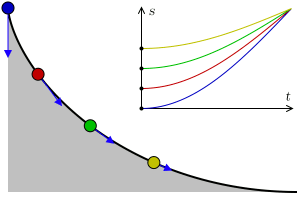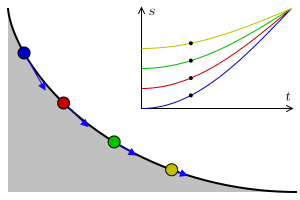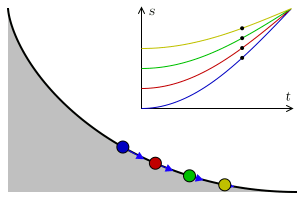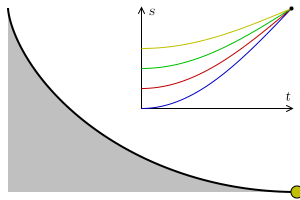
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a Cusp (singularity), cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brachistochrone
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a Cusp (singularity), cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brachistochrone Bernoulli Direct Method
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/Cole, 2012. 640. Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snell's Law
Snell's law (also known as Snell–Descartes law and ibn-Sahl law and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. This law was named after the Dutch astronomer and mathematician Willebrord Snellius (also called Snell). In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index. Snell's law states that, for a given pair of media, the ratio of the sines of angle of incidence (\theta_1 ) and angle of refraction (\theta_2 ) is equal to the refractive index of the second medium w.r.t the first (n21) which is equal to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Control
Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory. Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to calc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Minimal Resistance Problem
Newton's minimal resistance problem is a problem of finding a solid of revolution which experiences a minimum resistance when it moves through a homogeneous fluid with constant velocity in the direction of the axis of revolution, named after Isaac Newton, who studied the problem in 1685 and published it in 1687 in his Principia Mathematica. This is the first example of a problem solved in what is now called the calculus of variations, appearing a decade before the brachistochrone problem. Newton published the solution in Principia Mathematica without his derivation and David Gregory was the first person who approached Newton and persuaded him to write an analysis for him. Then the derivation was shared with his students and peers by Gregory. According to I Bernard Cohen, in his Guide to Newton’s Principia, "The key to Newton’s reasoning was found in the 1880s, when the earl of Portsmouth gave his family’s vast collection of Newton’s scientific and mathematical papers to Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tautochrone Curve
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono ''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius (of the circle which generates the cycloid) over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid. The tautochrone problem The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his ''Horologium Oscillatorium'', originally published in 1673, that the curve is a cycloid. The cycloid is given by a point on a circle of radius r tracing a curve as the circle rolls along the x axis, as: \begin x &= r(\theta - \sin \theta) \\ y &= r(1 - \cos \theta), \end Huygens al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Bernoulli
Johann Bernoulli (also known as Jean or John; – 1 January 1748) was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is known for his contributions to infinitesimal calculus and educating Leonhard Euler in the pupil's youth. Biography Early life Johann was born in Basel, the son of Nicolaus Bernoulli, an apothecary, and his wife, Margarethe Schongauer, and began studying medicine at University of Basel. His father desired that he study business so that he might take over the family spice trade, but Johann Bernoulli did not like business and convinced his father to allow him to study medicine instead. Johann Bernoulli began studying mathematics on the side with his older brother Jacob Bernoulli. Throughout Johann Bernoulli's education at Basel University the Bernoulli brothers worked together spending much of their time studying the newly discovered infinitesimal calculus. They were among the first mathematicians to not only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joseph-Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an and , later naturalized [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point. Similarly, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |