|
Bounded Complete
In the mathematical field of order theory, a partially ordered set is bounded complete if all of its subsets that have some upper bound also have a least upper bound. Such a partial order can also be called consistently or coherently complete ( Visser 2004, p. 182), since any upper bound of a set can be interpreted as some consistent (non-contradictory) piece of information that extends all the information present in the set. Hence the presence of some upper bound in a way guarantees the consistency of a set. Bounded completeness then yields the existence of a least upper bound of any "consistent" subset, which can be regarded as the most general piece of information that captures all the knowledge present within this subset. This view closely relates to the idea of information ordering that one typically finds in domain theory. Formally, a partially ordered set (''P'', ≤) is ''bounded complete'' if the following holds for any subset ''S'' of ''P'' : : If ''S'' has some up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Element And Least Element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set (poset) is an element of S that is greater than every other element of S. The term least element is defined dually, that is, it is an element of S that is smaller than every other element of S. Definitions Let (P, \leq) be a preordered set and let S \subseteq P. An element g \in P is said to be if g \in S and if it also satisfies: :s \leq g for all s \in S. By using \,\geq\, instead of \,\leq\, in the above definition, the definition of a least element of S is obtained. Explicitly, an element l \in P is said to be if l \in S and if it also satisfies: :l \leq s for all s \in S. If (P, \leq) is even a partially ordered set then S can have at most one greatest element and it can have at most one least element. Whenever a greatest element of S exists and is unique then this element is called greatest element of S. The terminology least element of S is defined simi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scott Domain
In the mathematical fields of order and domain theory, a Scott domain is an algebraic, bounded-complete cpo. They are named in honour of Dana S. Scott, who was the first to study these structures at the advent of domain theory. Scott domains are very closely related to algebraic lattices, being different only in possibly lacking a greatest element. They are also closely related to Scott information systems, which constitute a "syntactic" representation of Scott domains. While the term "Scott domain" is widely used with the above definition, the term "domain" does not have such a generally accepted meaning and different authors will use different definitions; Scott himself used "domain" for the structures now called "Scott domains". Additionally, Scott domains appear with other names like "algebraic semilattice" in some publications. Originally, Dana Scott demanded a complete lattice, and the Russian mathematician Yuri Yershov constructed the isomorphic structure of cpo. But ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximal Element
In mathematics, especially in order theory, a maximal element of a subset ''S'' of some preordered set is an element of ''S'' that is not smaller than any other element in ''S''. A minimal element of a subset ''S'' of some preordered set is defined dually as an element of ''S'' that is not greater than any other element in ''S''. The notions of maximal and minimal elements are weaker than those of greatest element and least element which are also known, respectively, as maximum and minimum. The maximum of a subset S of a preordered set is an element of S which is greater than or equal to any other element of S, and the minimum of S is again defined dually. In the particular case of a partially ordered set, while there can be at most one maximum and at most one minimum there may be multiple maximal or minimal elements. Specializing further to totally ordered sets, the notions of maximal element and maximum coincide, and the notions of minimal element and minimum coincide. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
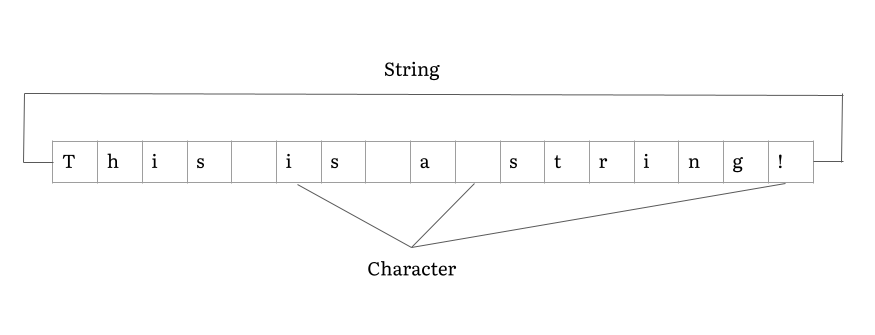
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Order
In mathematics, especially order theory, a prefix ordered set generalizes the intuitive concept of a tree by introducing the possibility of continuous progress and continuous branching. Natural prefix orders often occur when considering dynamical systems as a set of functions from ''time'' (a totally-ordered set) to some phase space. In this case, the elements of the set are usually referred to as ''executions'' of the system. The name ''prefix order'' stems from the prefix order on words, which is a special kind of substring relation and, because of its discrete character, a tree. Formal definition A prefix order is a binary relation "≤" over a set ''P'' which is antisymmetric, transitive, reflexive, and downward total, i.e., for all ''a'', ''b'', and ''c'' in ''P'', we have that: *''a ≤ a'' (reflexivity); *if ''a ≤ b'' and ''b ≤ a'' then ''a'' = ''b'' (antisymmetry); *if ''a ≤ b'' and ''b ≤ c'' then ''a ≤ c'' (transitivity); *if ''a ≤ c'' and ''b ≤ c'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal Number
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''. A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value. The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an integer, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Partial Order
In mathematics, the phrase complete partial order is variously used to refer to at least three similar, but distinct, classes of partially ordered sets, characterized by particular completeness properties. Complete partial orders play a central role in theoretical computer science: in denotational semantics and domain theory. Definitions A complete partial order, abbreviated cpo, can refer to any of the following concepts depending on context. * A partially ordered set is a directed-complete partial order (dcpo) if each of its directed subsets has a supremum. A subset of a partial order is directed if it is non-empty and every pair of elements has an upper bound in the subset. In the literature, dcpos sometimes also appear under the label up-complete poset. * A partially ordered set is a pointed directed-complete partial order if it is a dcpo with a least element. They are sometimes abbreviated cppos. * A partially ordered set is a ω-complete partial order (ω-cpo) if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Completeness (order Theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set (poset). The most familiar example is the completeness of the real numbers. A special use of the term refers to complete partial orders or complete lattices. However, many other interesting notions of completeness exist. The motivation for considering completeness properties derives from the great importance of suprema (least upper bounds, joins, "\vee") and infima (greatest lower bounds, meets, "\wedge") to the theory of partial orders. Finding a supremum means to single out one distinguished least element from the set of upper bounds. On the one hand, these special elements often embody certain concrete properties that are interesting for the given application (such as being the least common multiple of a set of numbers or the union of a collection of sets). On the other hand, the knowledge that certain types of subsets are guara ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain Theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets (posets) commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational semantics, especially for functional programming languages. Domain theory formalizes the intuitive ideas of approximation and convergence in a very general way and is closely related to topology. Motivation and intuition The primary motivation for the study of domains, which was initiated by Dana Scott in the late 1960s, was the search for a denotational semantics of the lambda calculus. In this formalism, one considers "functions" specified by certain terms in the language. In a purely syntactic way, one can go from simple functions to functions that take other functions as their input arguments. Using again just the syntactic transformations available in this formalism, one can o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Visser2004
Visser is a Dutch occupational surname, meaning "fisherman". In 2007, nearly 50,000 people in the Netherlands carried the name, making it the eighth most populous name in the country. at the Database of Surnames in The Netherlands. Common variant forms of the name are '''', '''', and ''''. Geographical distribution As of 2014, 43.7% of all known bearers of the surname ''Visser'' were residents of So ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |