|
Bertus Brouwer
Luitzen Egbertus Jan Brouwer (; ; 27 February 1881 – 2 December 1966), usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, who worked in topology, set theory, measure theory and complex analysis. Regarded as one of the greatest mathematicians of the 20th century, he is known as the founder of modern topology, particularly for establishing his fixed-point theorem and the topological invariance of dimension. Brouwer also became a major figure in the philosophy of intuitionism, a constructivist school of mathematics which argues that math is a cognitive construct rather than a type of objective truth. This position led to the Brouwer–Hilbert controversy, in which Brouwer sparred with his formalist colleague David Hilbert. Brouwer's ideas were subsequently taken up by his student Arend Heyting and Hilbert's former student Hermann Weyl. Biography Brouwer was born to Dutch Protestant parents. Early in his career, Brouw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overschie
Overschie is a neighborhood of Rotterdam, Netherlands, formerly a separate village with its own municipality. The village of Overschie was located on the intersection of four rivers called "Schie": the Delftsche Schie, Schiedamsche Schie, Delfshavensche Schie, and Rotterdamsche Schie. It was a separate municipality between 1817 and 1941, when it merged with Rotterdam. Immediately after the Second World War, the construction of a large suburb was begun southeast of the village. "Overschie" is now also the name of a ''deelgemeente'' (borough) of the city of Rotterdam, covering the former village, the neighborhood Overschie, Zestienhoven (which also holds the Rotterdam The Hague Airport Rotterdam The Hague Airport (formerly ''Rotterdam Airport'', ''Vliegveld Zestienhoven'' in Dutch), is a minor international airport serving Rotterdam, the Netherlands' second largest city, and The Hague, its administrative and royal capital. I ...), and the countryside to the north including ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene–Brouwer Order
In descriptive set theory, the Kleene–Brouwer order or Lusin–Sierpiński order is a linear order on finite sequences over some linearly ordered set (X, <), that differs from the more commonly used in how it handles the case when one sequence is a of the other. In the Kleene–Brouwer order, the prefix is later than the longer sequence containing it, rather than earlier. The Kleene–Brouwer order generalizes the notion of a from finite trees to trees that are not necessarily finite. For trees over a well-ordered set, the Kleene–Brouwer order is i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biographical Memoirs Of Fellows Of The Royal Society
The ''Biographical Memoirs of Fellows of the Royal Society'' is an academic journal on the history of science published annually by the Royal Society. It publishes obituaries of Fellows of the Royal Society. It was established in 1932 as ''Obituary Notices of Fellows of the Royal Society'' and obtained its current title in 1955, with volume numbering restarting at 1. Prior to 1932, obituaries were published in the ''Proceedings of the Royal Society''. The memoirs are a significant historical record and most include a full bibliography of works by the subjects. The memoirs are often written by a scientist of the next generation, often one of the subject's own former students, or a close colleague. In many cases the author is also a Fellow. Notable biographies published in this journal include Albert Einstein, Alan Turing, Bertrand Russell, Claude Shannon, Clement Attlee, Ernst Mayr, and Erwin Schrödinger. Each year around 40 to 50 memoirs of deceased Fellows of the Royal Soci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society
The Royal Society, formally The Royal Society of London for Improving Natural Knowledge, is a learned society and the United Kingdom's national academy of sciences. The society fulfils a number of roles: promoting science and its benefits, recognising excellence in science, supporting outstanding science, providing scientific advice for policy, education and public engagement and fostering international and global co-operation. Founded on 28 November 1660, it was granted a royal charter by King Charles II as The Royal Society and is the oldest continuously existing scientific academy in the world. The society is governed by its Council, which is chaired by the Society's President, according to a set of statutes and standing orders. The members of Council and the President are elected from and by its Fellows, the basic members of the society, who are themselves elected by existing Fellows. , there are about 1,700 fellows, allowed to use the postnominal title FRS (Fellow of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism (opposed to preintuitionism), is an approach where mathematics is considered to be purely the result of the constructive mental activity of humans rather than the discovery of fundamental principles claimed to exist in an objective reality. That is, logic and mathematics are not considered analytic activities wherein deep properties of objective reality are revealed and applied, but are instead considered the application of internally consistent methods used to realize more complex mental constructs, regardless of their possible independent existence in an objective reality. Truth and proof The fundamental distinguishing characteristic of intuitionism is its interpretation of what it means for a mathematical statement to be true. In Brouwer's original intuitionism, the truth of a mathematical statement is a subjective claim: a mathematical statement corresponds to a mental construction, and a mathematician can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
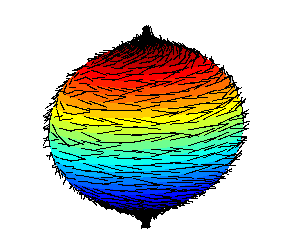
Hairy Ball Theorem
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional ''n''-spheres. For the ordinary sphere, or 2‑sphere, if ''f'' is a continuous function that assigns a vector in R3 to every point ''p'' on a sphere such that ''f''(''p'') is always tangent to the sphere at ''p'', then there is at least one pole, a point where the field vanishes (a ''p'' such that ''f''(''p'') = 0). The theorem was first proved by Henri Poincaré for the 2-sphere in 1885, and extended to higher dimensions in 1912 by Luitzen Egbertus Jan Brouwer. The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut". Counting zeros Every zero of a vector field has a (non-zero) " index", and it can be shown that the sum of all of the indices at all of the zeros must be two, because the Euler char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spread (intuitionism)
In intuitionistic mathematics, a ''species'' is a collection (similar to a classical set in that a species is determined by its members). A spread is a particular kind of species of infinite sequences defined via finite decidable properties. In modern terminology, a spread is an inhabited closed set of sequences. The notion of spread was first proposed by L. E. J. Brouwer (1918B), and was used to define the real numbers (also called the continuum). As Brouwer's ideas were developed, the use of spreads became common in intuitionistic mathematics, especially when dealing with choice sequences and the foundations of intuitionistic analysis (Dummett 77, Troelstra 77). Simple examples of spreads are: *the set of sequences of even numbers; *the set of sequences of the integers 1–6; *the set of sequences of valid terminal commands. Spreads are defined via a ''spread function'', which performs a ( decidable) "check" on finite sequences. The notion of a spread and its spread f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariance Of Domain
Invariance of domain is a theorem in topology about homeomorphic subsets of Euclidean space \R^n. It states: :If U is an open subset of \R^n and f : U \rarr \R^n is an injective continuous map, then V := f(U) is open in \R^n and f is a homeomorphism between U and V. The theorem and its proof are due to L. E. J. Brouwer, published in 1912. The proof uses tools of algebraic topology, notably the Brouwer fixed point theorem. Notes The conclusion of the theorem can equivalently be formulated as: "f is an open map". Normally, to check that f is a homeomorphism, one would have to verify that both f and its inverse function f^ are continuous; the theorem says that if the domain is an subset of \R^n and the image is also in \R^n, then continuity of f^ is automatic. Furthermore, the theorem says that if two subsets U and V of \R^n are homeomorphic, and U is open, then V must be open as well. (Note that V is open as a subset of \R^n, and not just in the subspace topology. Openness ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indecomposable Continuum
In point-set topology, an indecomposable continuum is a continuum that is indecomposable, i.e. that cannot be expressed as the union of any two of its proper subcontinua. In 1910, L. E. J. Brouwer was the first to describe an indecomposable continuum. Indecomposable continua have been used by topologists as a source of counterexamples. They also occur in dynamical systems. Definitions A ''continuum'' C is a nonempty compact connected metric space. The arc, the ''n''-sphere, and the Hilbert cube are examples of path-connected continua; the topologist's sine curve and Warsaw circle are examples of non-path-connected continua. A ''subcontinuum'' C' of a continuum C is a closed, connected subset of C. A space is ''nondegenerate'' if it is not equal to a single point. A continuum C is ''decomposable'' if there exist two nondegenerate subcontinua A and B of C such that A \neq C and B \neq C but A \cup B = C. A continuum that is not decomposable is an ''indecomposable continuum''. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indecomposability (constructive Mathematics)
In intuitionistic analysis and in computable analysis, indecomposability or indivisibility (german: Unzerlegbarkeit, from the adjective ''unzerlegbar'') is the principle that the continuum cannot be partitioned into two nonempty pieces. This principle was established by Brouwer in 1928 English translation of §1 see p.490–492 of: using intuitionistic principles, and can also be proven using Church's thesis. The analogous property in classical analysis is the fact that every continuous function from the continuum to is constant. It follows from the indecomposability principle that any property of real numbers that is ''decided'' (each real number either has or does not have that property) is in fact trivial (either all the real numbers have that property, or else none of them do). Conversely, if a property of real numbers is not trivial, then the property is not decided for all real numbers. This contradicts the law of the excluded middle, according to which every propert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Continuous Mapping
In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations. The degree of a map was first defined by Brouwer, who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number. Definitions of the degree From ''S''''n'' to ''S''''n'' The simplest and most important case is the degree of a continuous map from the n-sphere S^n to itself (in the case n=1, this is called the winding number): Let f\colon S^n\t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bar Induction
Bar induction is a reasoning principle used in intuitionistic mathematics, introduced by L. E. J. Brouwer. Bar induction's main use is the intuitionistic derivation of the fan theorem, a key result used in the derivation of the uniform continuity theorem. It is also useful in giving constructive alternatives to other classical results. The goal of the principle is to prove properties for all infinite sequences of natural numbers (called choice sequences in intuitionistic terminology), by inductively reducing them to properties of finite lists. Bar induction can also be used to prove properties about all choice sequences in a spread (a special kind of set). Definition Given a choice sequence x_0,x_1,x_2,x_3,\ldots, any finite sequence of elements x_0,x_1,x_2,x_3,\ldots,x_i of this sequence is called an ''initial segment'' of this choice sequence. There are three forms of bar induction currently in the literature, each one places certain restrictions on a pair of predicates a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |